⚛️ ✖️ ✉️ Paradoks ulang tahun pada data VK 🥋 🏣 🦖

Halo!

Saya memutuskan untuk memeriksa paradoks ulang tahun menggunakan data yang tersedia dari VK.

Apa itu paradoks ulang tahun?

Cobalah untuk menjawab pertanyaan: Berapa banyak orang di sebuah ruangan yang diperlukan agar dua orang memiliki ulang tahun yang sama dengan probabilitas 0,5? (tanggal dan bulan). Paradoks ulang tahun menjawab pertanyaan ini.

Untuk mengatasi masalah, perlu menyoroti beberapa prasyarat:

Model tidak akan memiliki 29 Februari => 365 hari setahun dalam model
Masing-masing dari 365 hari kemungkinan sama.

Tentu saja, itu tidak sepenuhnya realistis bahwa ulang tahun sama-sama memungkinkan - ada efek musiman yang mempengaruhi tanggal kelahiran anak-anak, saya pikir Anda sendiri dapat menebak yang mana ...

Kebanyakan orang secara intuitif menjawab pertanyaan tentang masalah: 180. Tampaknya logis, 180 orang diperlukan untuk memiliki probabilitas 0,5 ulang tahun identik (total 365 hari). Setiap orang yang belum pernah mendengar tentang paradoks ulang tahun adalah tentang intuisi ini. Jawaban yang benar sebenarnya jauh lebih sedikit dari 180, dan bahkan 150, dan bahkan 100: 23.

Diperlukan setidaknya 1 ulang tahun yang cocok - jadi saya dapat menemukan probabilitas bahwa tidak ada ulang tahun yang cocok:

P (" р а з л и ч н ы е Д Р ") = \frac{365 * 364 * 363 * . . . * (365 - k + 1)}{365^{k}} = \frac{365!}{365^{k} * (365 - k)!}

$P(" \space ") = \frac {365 * 364 * 363 * ... * (365 - k + 1)} {365 ^ k} = \frac {365!} {365^k * (365 - k)!}$

...

Idenya adalah ini: Saya mengambil orang pertama dan mengingat hari ulang tahunnya, kemudian yang kedua dan menghitung probabilitas bahwa hari ulang tahunnya tidak bersamaan dengan hari ulang tahun orang pertama; lebih jauh dari yang ketiga dan saya menghitung probabilitas bahwa hari ulang tahunnya tidak bersamaan dengan hari ulang tahun pertama dan kedua.

Memecahkan persamaan, ternyata 23 orang diperlukan dan probabilitas bertepatan ulang tahun akan menjadi 0,5073, dengan 100 orang, probabilitasnya adalah 0,9999.

Mari kita lihat paradoks pada data VK?

Secara teori, dengan 23 orang, probabilitas bertepatan ulang tahun adalah 0,5073, dengan 50 orang 0,97, dan dengan 100 0,99. Mari kita periksa melalui VK API.

1. Saya memilih komunitas besar di VK. Saya memutuskan untuk mengambil grup MDK di Vkontakte ...

Pertama, saya membuat file csv dengan kolom yang saya butuhkan.

with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()

Saya masuk ke VK melalui API dan mengatur publik yang saya butuhkan

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')

Kami mulai mem-parsing VKontakte, API mereka memungkinkan Anda untuk mem-parsing hanya 1000 pengguna, jadi saya membuat loop.

for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass

Secara teori, kami berasumsi bahwa ulang tahun sama-sama memungkinkan, tetapi apa yang terjadi dalam praktik? Saya akan membuat histogram ulang tahun.

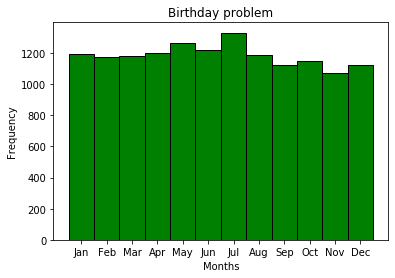
gambar

Ulang tahun per bulan bukanlah acara yang bisa disetel, yang umumnya cukup logis - ini hanya prasyarat untuk menyelesaikan masalah ulang tahun. Jelas, akan ada acara musiman yang berbeda, untuk lokasi yang berbeda. Untuk beberapa alasan, Juli adalah bulan paling populer untuk ulang tahun pelanggan MDK.

Saya secara empiris akan memperkirakan probabilitas bahwa dalam kelompok 50 orang sewenang-wenang setidaknya ada dua dengan ulang tahun yang sama. Untuk melakukan ini, saya menulis siklus di mana sub-sampel 50 baris muncul dari tabel. Untuk 50 baris ini di dalam kondisi, saya memeriksa pertandingan ulang tahun. Jika cocok, maka saya mengingatnya dalam variabel counter, yang kemudian akan saya bagi dengan panjang siklus untuk mendapatkan probabilitas.

fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)

Probabilitas diperoleh di wilayah 0,97, yang bertepatan dengan data teoritis.

Keluaran

Sangat menarik untuk melihat bagaimana teori berhubungan dengan empirisme, dan dalam hal ini data mengkonfirmasi teori tersebut. Perlu dicatat bahwa hasilnya representatif, karena sampelnya cukup besar - 20.000 orang.

Sumber daya

Universitas Harvard. Masalah Ulang Tahun, Sifat Probabilitas | Statistik 110. URL: www.youtube.com/watch?v=LZ5Wergp_PA&t=150s . Diakses: 07/08/2020
Masalah ulang tahun URL: en.wikipedia.org/wiki/Birthday_problem . Diakses: 07/08/2020>

Paradoks ulang tahun pada data VK

Apa itu paradoks ulang tahun?

Mari kita lihat paradoks pada data VK?

Keluaran

Sumber daya

More articles: