
Terimakasih banyak. Saya minta maaf karena duduk di sini. Saya orang yang sangat tua.
Topik saya hari ini dalam arti sangat istimewa, karena sangat kuno. Kinks adalah bagian integral dari kehidupan manusia, mereka selalu ada. Orang dahulu menulis tentang ini. Hal ini sebagian besar di luar kendali kami. Dan dalam arti tertentu, mereka tampaknya tingkat komplikasi yang ekstrem - hanya kekacauan total.
Ada banyak jenis gangguan. Jadi, karena kebetulan murni, bertahun-tahun yang lalu saya mulai berurusan dengan bentuk kerumitan ini, dan, yang sangat mengejutkan saya, saya menemukan tanda-tanda, dan, harus saya katakan, tanda-tanda keteraturan yang sangat jelas dalam kekusutan. Jadi hari ini saya ingin menyampaikan kepada Anda beberapa contoh apa artinya ini. Saya lebih suka kata "patah" menjadi "tidak rata" karena, bagi seseorang yang belajar bahasa Latin, seperti saya di masa muda saya yang jauh, ketidakmerataan adalah kebalikan dari kemerataan. Tapi ini bukan masalahnya.
Kesetaraan adalah kebalikan dari fraktur, karena dunia sebagian besar bagi kita tampak penuh dengan fraktur.
Mari saya tunjukkan beberapa objek. Beberapa dari mereka dibuat secara buatan. Yang lain sangat nyata, dalam arti tertentu. Ini yang asli.

Ini bunga kol. Mengapa saya menunjukkan Anda kembang kol, tanaman biasa dan kuno? Karena, meskipun rutin dan kuno, itu kompleks dan sederhana. itu rumit dan sederhana. Misalnya, tidak sulit untuk menimbangnya. Berat penting jika kita akan memakannya. Tapi anggaplah kita akan mengukur permukaannya. Ini semakin menarik. Setelah memotong salah satu bunga kembang kol dengan pisau tajam, dan melihat dari dekat, kami melihat keseluruhan kembang kol, hanya berukuran lebih kecil. Kemudian Anda dapat memotong lagi dan lagi dan lagi dan lagi dan lagi ... Dan Anda mendapatkan spesimen kembang kol yang lebih kecil dan lebih kecil. Pengalaman manusia telah menunjukkan bahwa ada bentuk-bentuk dengan sifat yang menarik sehingga setiap bagian mirip dengan keseluruhan, tetapi dengan ukuran yang lebih kecil. Dan apa yang orang pelajari dari fakta ini? Sangat kecil.
Sehubungan dengan studi masalah ini, saya menemukan sesuatu yang sangat menakjubkan: ketegaran dapat diukur dengan angka, katakanlah, 2,3 atau 1,2, dan kadang-kadang jauh lebih banyak. Suatu hari, seorang teman saya membawa foto dan, setengah bercanda, bertanya: "Apa lengkungan kurva ini?" Saya berkata, "Sedikit kurang dari satu setengah." Ternyata, itu sama dengan 1,48. Tidak butuh waktu lama bagi saya untuk mempelajari hal-hal ini begitu lama. Angka-angka dalam pertanyaan menunjukkan tingkat fraktur permukaan.

Biarkan saya membuat reservasi segera bahwa permukaan benar-benar buatan dan dibuat di komputer. Satu-satunya titik awal adalah angka. Jumlah ini ketegaran. Fraktur di sebelah kiri adalah hasil penyalinan dari beberapa lanskap. Di sebelah kanan - saya mengatur ketegaran yang lebih tinggi sendiri. Jika Anda perhatikan dengan seksama, setelah beberapa saat Anda dapat mengenali perbedaan dalam dua kasus ini dengan mata telanjang.
Manusia harus terbiasa dengan konsep patah tulang. Ini sangat rusak, tetapi ini, bisa dikatakan, halus, tetapi ini sepenuhnya mulus. Beberapa hal sangat halus. Mari kita tanyakan pada diri sendiri pertanyaan: apa permukaan kembang kol? Ini dapat diukur dan diukur dan diukur ... Semakin akurat pengukuran, semakin besar permukaannya, dan seterusnya, hingga jarak yang sangat kecil. Berapa panjang garis pantai dari danau-danau ini? Semakin akurat pengukuran, semakin lama hasilnya. Konsep panjang garis pantai, yang tampak begitu jelas karena sering dikutip, sebenarnya sepenuhnya salah: sama sekali tidak ada hal seperti itu. Harus ada pendekatan yang berbeda.
Dan apa gunanya pengetahuan ini? Anehnya, ada banyak manfaatnya. Untuk mulai dengan, lanskap buatan yang saya, harus kita katakan, telah diciptakan terus-menerus digunakan dalam sinematografi. Kami melihat gunung di kejauhan. Mungkin gunung, tetapi mungkin hanya formula yang mengalir. Ini sangat mudah dicapai. Dulu butuh waktu lama, tapi sekarang itu hanya hal sepele. Coba lihat di sini. Ini cahaya yang nyata.
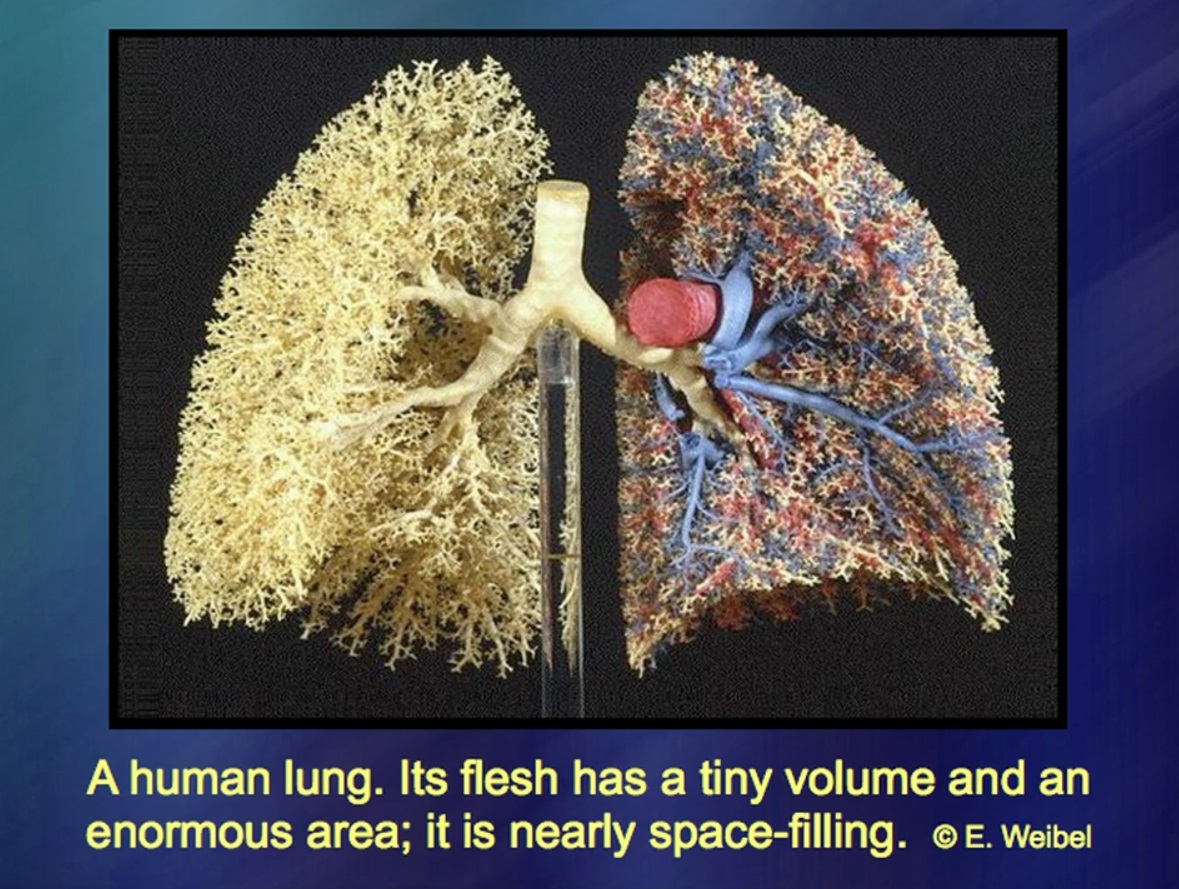
Paru-paru adalah benda yang sangat aneh. Kita semua tahu betul bahwa beratnya sedikit. Diketahui juga bahwa volume paru-paru sangat kecil. Bagaimana dengan area paru-paru? Para ahli anatomi telah lama memperdebatkan masalah ini. Dipercayai bahwa pada pria normal, luas paru-paru sama dengan luas satu bola basket. Yang lain berpendapat bahwa tidak ada lima bola seperti itu. Perbedaan itu sangat besar. Mengapa? Karena area paru-paru adalah konsep yang sangat samar. Cabang dan cabang bronkus semakin dalam dan semakin dalam. Dan mereka berhenti bercabang bukan karena beberapa prinsip, tetapi karena kondisi fisik murni, karena lendir di dalam paru-paru. Ini adalah bagaimana paru-paru yang jauh lebih besar terbentuk: cabang bronkus keluar lebih dalam dan lebih dalam sampai jarak di antara mereka kira-kira sama untuk paus, dan untuk seseorang, dan untuk tikus kecil.
Jadi apa gunanya ini? Yang mengejutkan dan bahkan mengejutkan, ahli anatomi memiliki gagasan yang buruk tentang struktur paru-paru sampai saat ini. Saya pikir penelitian matematis saya, cukup mengejutkan, sangat membantu ahli bedah yang mempelajari penyakit paru-paru, serta penyakit hati, di mana ada sistem cabang seperti itu dengan kurangnya geometri yang dapat dipahami. Dengan kata lain, saya harus membuat geometri untuk sesuatu yang tidak memiliki geometri sendiri. Kualitas mengejutkan ditemukan: sangat sering aturan geometri ini sangat ringkas. Anda mulai dengan formula pendek, menerapkannya beberapa kali, kadang berulang kali, berulang-ulang. Pengulangan yang sama. Dan pada akhirnya ternyata seperti itu.
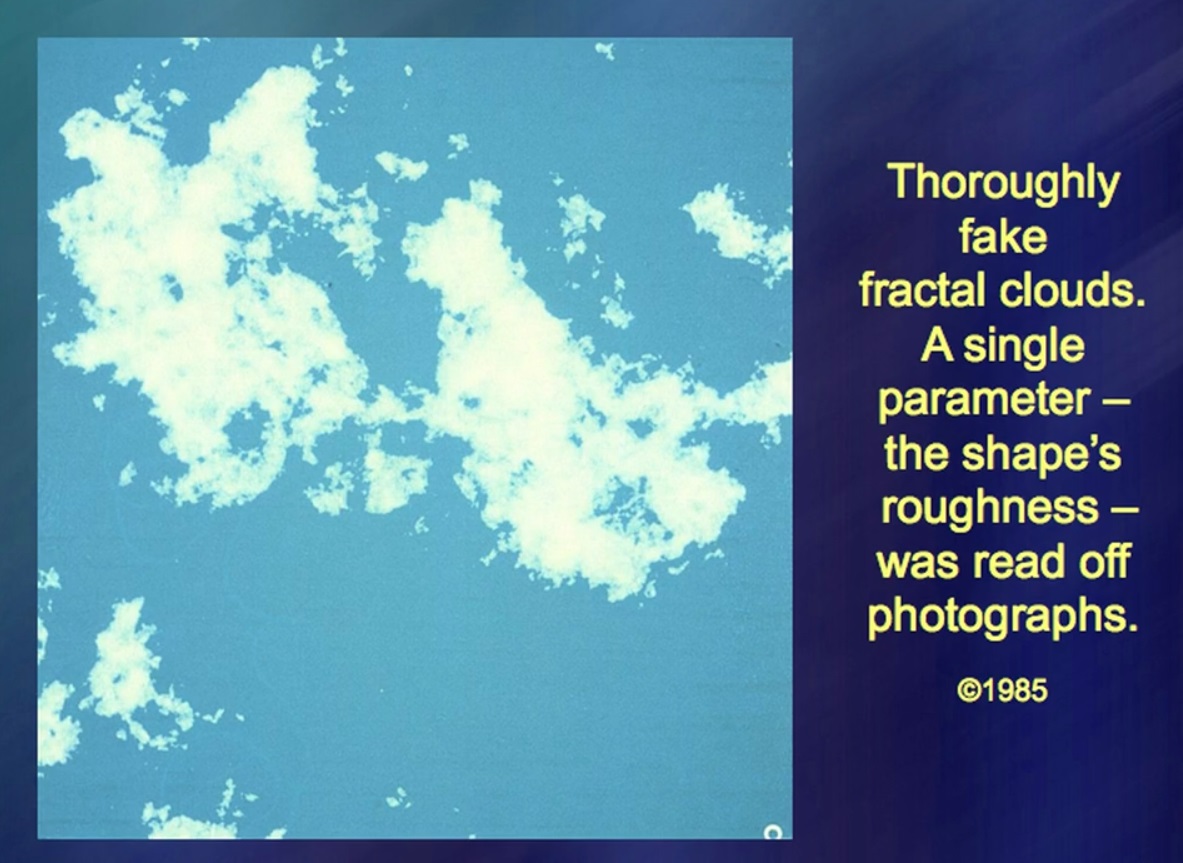
Awan ini sepenuhnya buatan, 100%. Oke, 99,9%. Satu-satunya unsur alami di sini adalah angka, fraktur awan - angka ini diambil dari alam. Hal yang sangat rumit seperti awan, sangat tidak stabil, dapat berubah, mematuhi aturan sederhana. Aturan sederhana ini bukan penjelasan untuk kekeruhan. Tetapi lautan awan harus memperhitungkan aturan ini. Saya tidak tahu seberapa sempurna foto-foto lama ini. Saya melakukan ini secara intensif, tetapi kemudian perhatian saya diarahkan ke fenomena lain.
Dan ini satu hal lagi yang menarik. Salah satu peristiwa revolusioner dalam sejarah matematika, yang kurang dihargai oleh banyak orang, terjadi sekitar 130 tahun yang lalu, 145 tahun yang lalu. Matematikawan mulai membuat bentuk yang tidak ada. Di antara matematikawan, kemampuan seseorang untuk menciptakan sesuatu yang tidak pernah ada di alam menjadi sangat dihargai, dan pada tingkat yang benar-benar tak terbayangkan. Secara khusus, mereka mampu menciptakan kurva yang mengisi seluruh bidang ke titik terakhir. Kurva adalah kurva, bidang adalah bidang, dan keduanya tidak saling cocok. Ternyata mereka cocok satu sama lain.
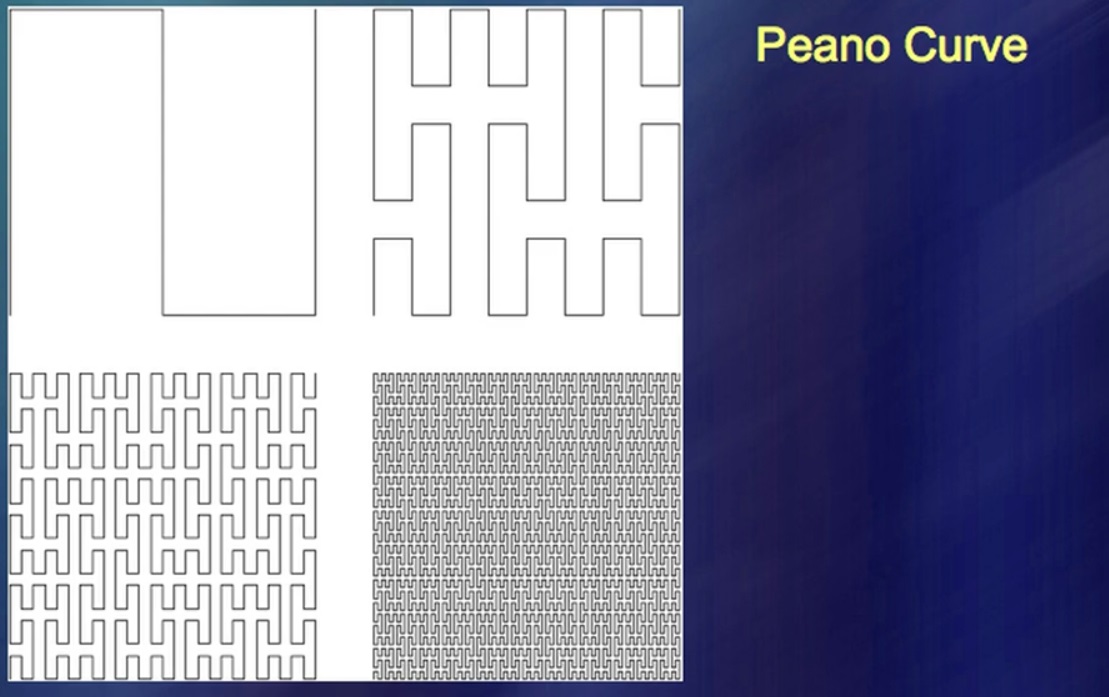
Seorang pria bernama Peano mengidentifikasi kurva seperti itu, dan mereka menghasilkan minat yang luar biasa. Mereka sangat penting dan membangkitkan minat sebagian besar karena telah ada semacam pembagian matematika menjadi satu didasarkan pada kenyataan dan satu yang berasal dari alasan murni. Sayangnya, saya kebetulan membuktikan bahwa apa yang diketahui melalui upaya akal murni, pada kenyataannya, telah lama dikenal dalam bentuk yang berbeda. Di sini saya memiliki sistem anak sungai dalam bentuk kurva mengisi pesawat.

Dalam dirinya sendiri, ini adalah sejarah. Itu antara 1875 dan 1925, waktu yang menakjubkan ketika matematika sedang bersiap untuk melepaskan diri dari dunia nyata. Benda-benda tertentu telah berfungsi sebagai ilustrasi kesenjangan, sejak masa kanak-kanak saya dan murid-murid saya tahun, kesenjangan antara matematika dan kenyataan yang terlihat. Namun, saya berhasil memikirkan kembali mereka, membalikkannya, dan dengan bantuan mereka menggambarkan beberapa aspek kompleksitas alam.
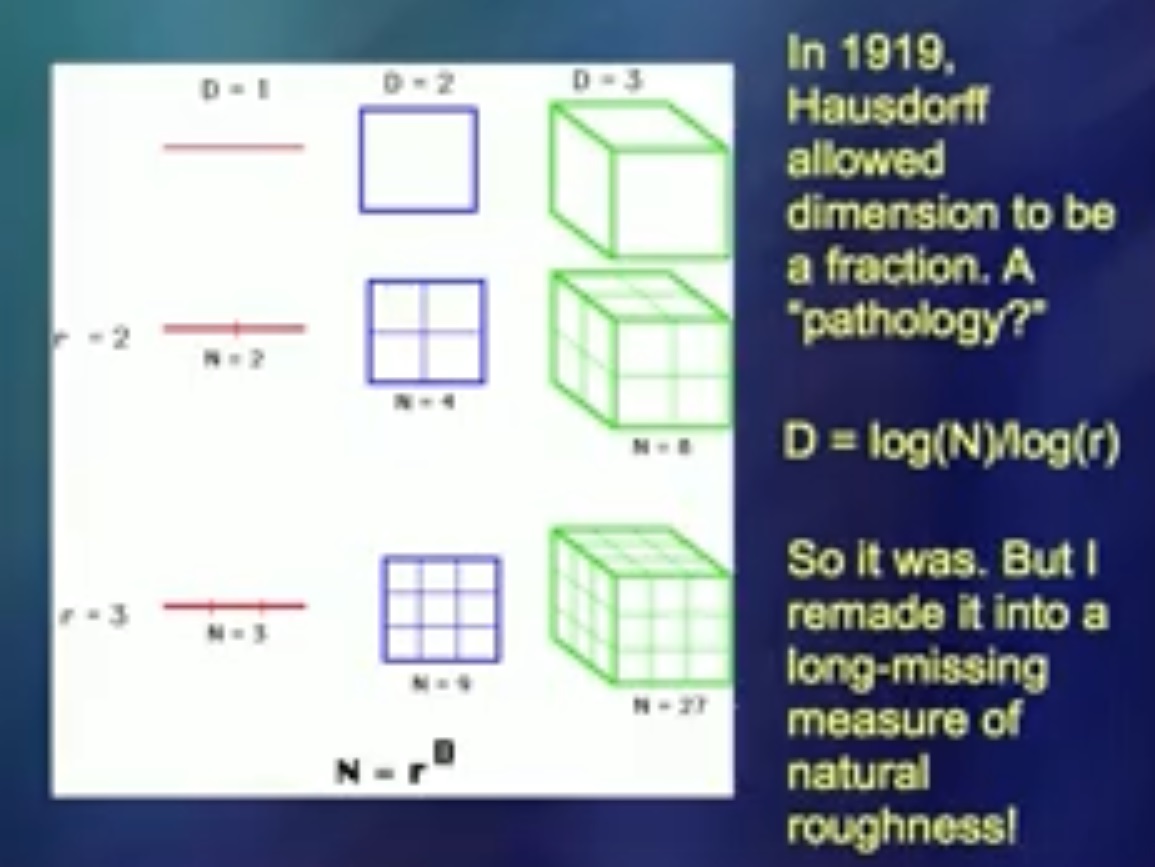
Pada 1919, seorang pria bernama Hausdorff mengidentifikasi nomor yang bisa dianggap sebagai lelucon matematika. Tetapi saya telah menemukan bahwa angka ini adalah alat yang baik untuk mengukur ketegaran. Ketika saya pertama kali memberi tahu kolega saya tentang hal ini, mereka berkata, “Jangan konyol. Ini sesuatu ... ”Sebenarnya, saya tidak melakukan hal-hal bodoh.

Artis hebat Hokusai tahu ini dengan sangat baik. Di bagian bawah gambar adalah ganggang. Hokusai tidak tahu matematika yang diperlukan: itu hanya tidak ada saat itu. Selain itu, sebagai orang Jepang, ia [saat itu] tidak memiliki kontak dengan Barat. Tetapi seni telah lama mengandung elemen fraktal. Saya bisa membicarakan ini untuk waktu yang lama.

Menara Eiffel memiliki elemen fraktal. Saya membaca buku Eiffel tentang menara-nya - ruang lingkup pemahamannya luar biasa.
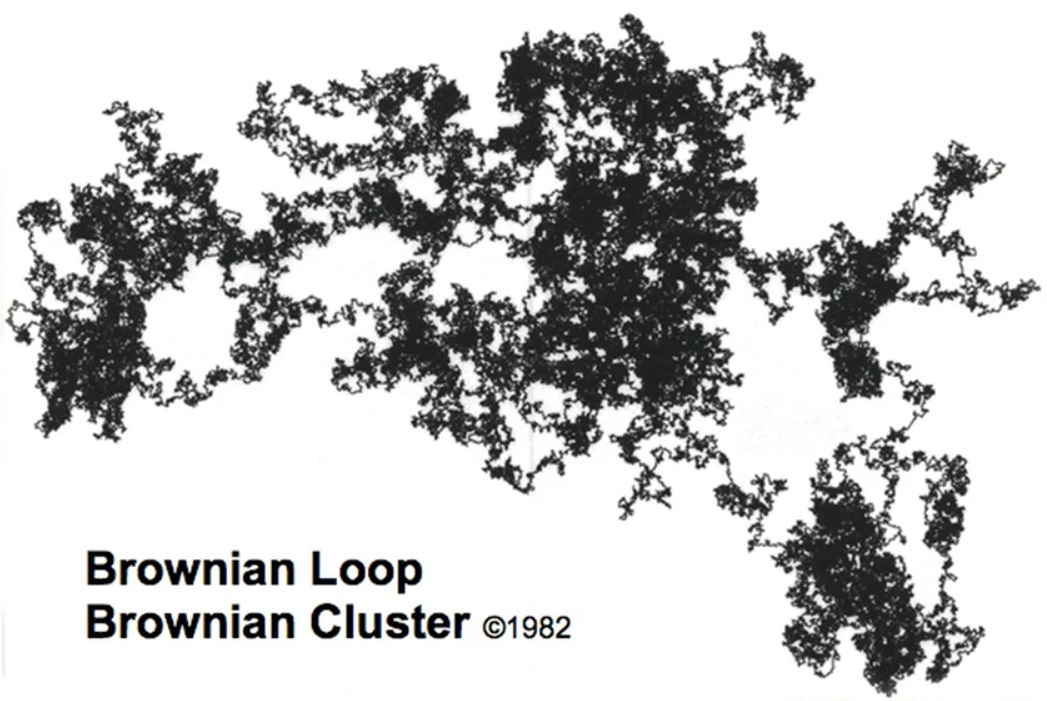
Ini adalah kekacauan di dalam kekacauan. Lingkaran brown. Suatu kali saya memutuskan bahwa saya telah menjalani sebagian besar kehidupan profesional saya, dan begitu banyak hal yang berbeda menyibukkan saya sehingga saya memutuskan bahwa sudah waktunya untuk menguji diri saya. Dapatkah saya menjelajahi objek yang sudah lama dijelajahi semua orang dan menemukan sesuatu yang baru secara radikal di dalamnya? Saya mulai mempelajari segala sesuatu yang termasuk dalam kategori gerak Brown. Saya mencoba sudut yang berbeda, mencoba metode yang berbeda, dan kembali ke tempat saya mulai. Kemudian saya menyarankan kepada asisten saya: “Saya tidak melihat apa pun di sini. Bisakah kamu melukis? Dia melakukannya, yaitu, dia mengisi semua bagian dalamnya. "Saya mengatur…"

Tetapi saya berteriak: “Berhenti! Berhenti! Berhenti! Dipahami: ini adalah sebuah pulau. " Luar biasa. Gerakan Brown memiliki kekakuan sama dengan dua. Saya mengukurnya, ternyata 1,33. Saya mengukur lagi dan lagi. Pengukuran panjang, gerakan Brown yang besar. Lagi: 1.33. Masalah matematika segera muncul: bagaimana cara membuktikannya? Butuh teman-teman saya 20 tahun. Tiga memiliki bukti yang tidak lengkap. Mereka bergabung dan bersama-sama mereka berhasil mendapatkan bukti. Akibatnya, mereka dianugerahi medali [Fields] terkenal untuk ahli matematika. Secara keseluruhan, matematikawan menerima tiga medali [Bidang] untuk membuktikan fakta yang saya lihat tetapi tidak bisa membuktikan.
Sekarang orang bertanya kepada saya di mana-mana: “Bagaimana semuanya dimulai? Bagaimana studi Anda mengarahkan Anda ke hal-hal yang tidak biasa seperti itu? "
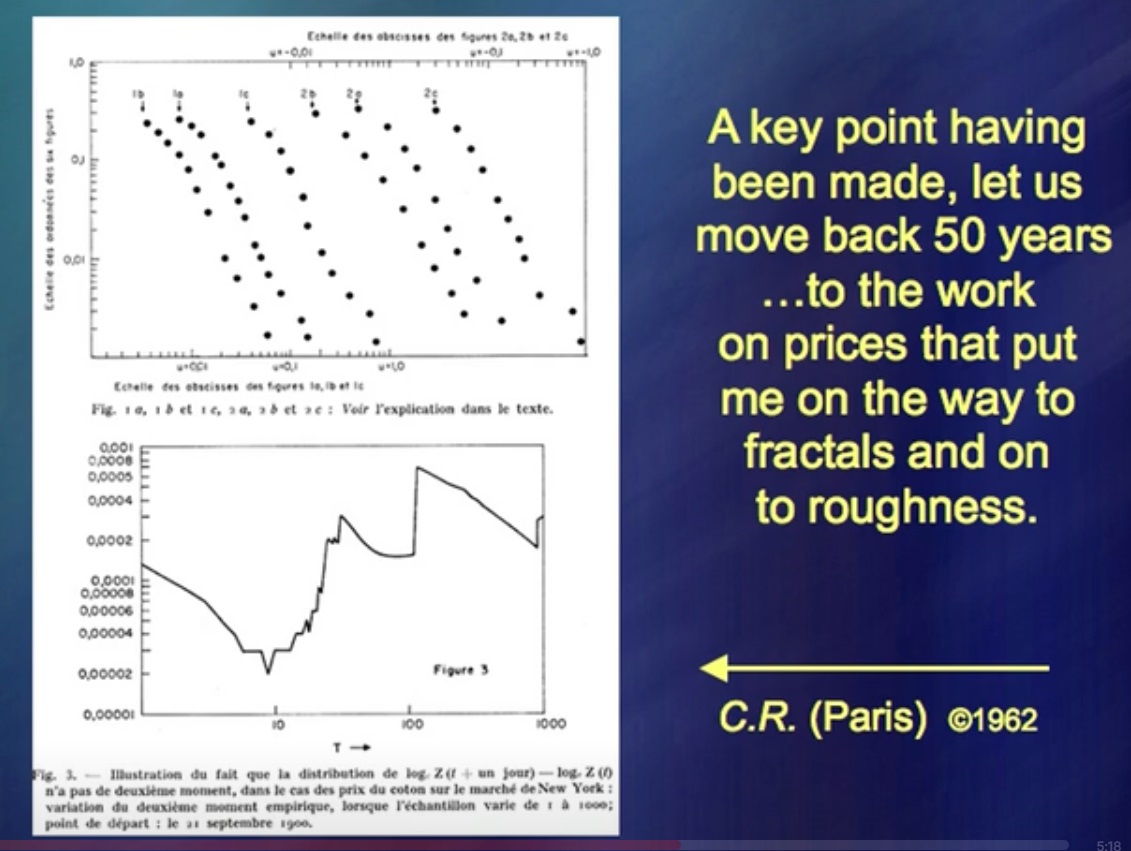
Apa yang memungkinkan saya untuk secara bersamaan menjadi insinyur mesin, ahli geografi, ahli matematika, dll.? Cukup aneh, tetapi saya mulai dengan mempelajari harga di pasar saham.

Saya punya teori dan saya menulis buku tentang itu.
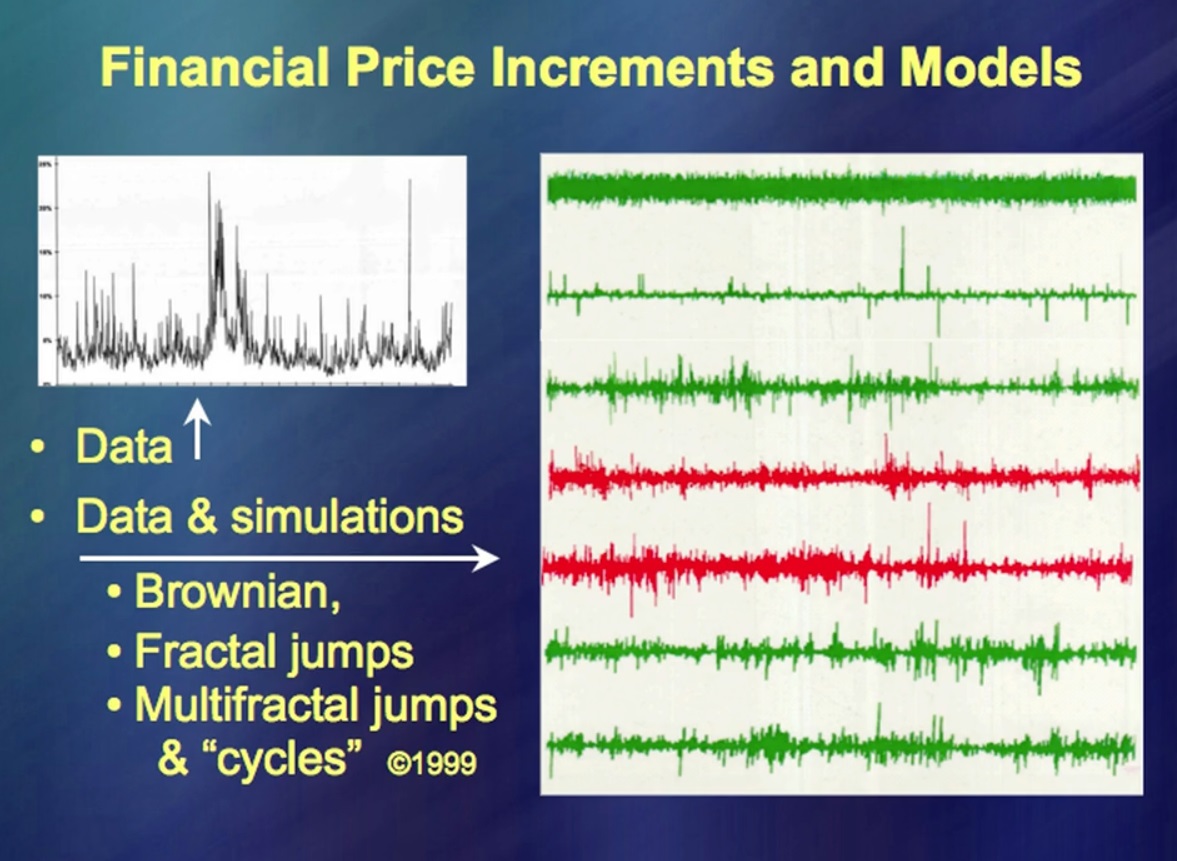
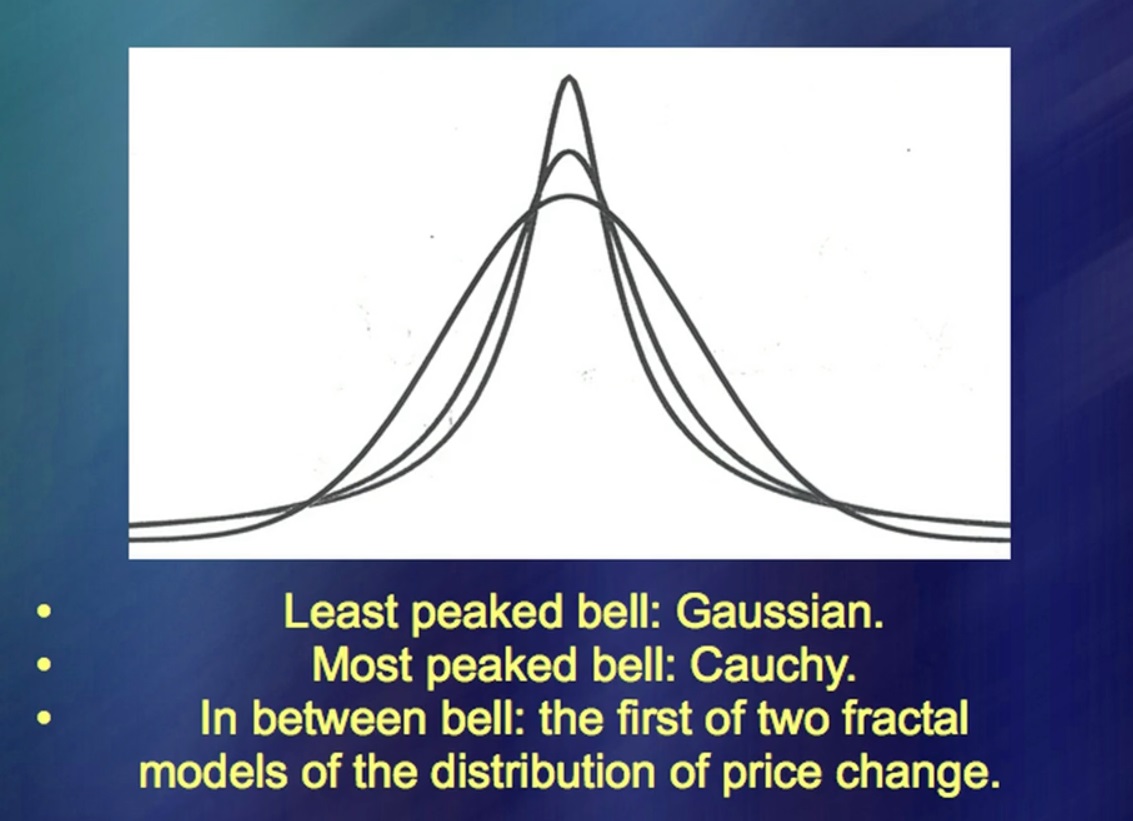
"Pergerakan harga instrumen keuangan" Di sebelah kiri Anda dapat melihat data untuk jangka waktu lama, di sebelah kanan, di atas - data menurut teori yang sangat, sangat modis. Ini sangat sederhana dan Anda dapat menulis banyak buku tentangnya dengan sangat cepat. (Tawa) Ada ribuan buku tentang topik ini. Sekarang bandingkan dengan pergerakan harga riil. Dan dimana mereka? Baris tambahan termasuk pergerakan harga riil serta palsu kecil di pihak saya. Gagasan utama di sana adalah bahwa Anda harus bisa melakukan ... Apa namanya? ... Simulasi fluktuasi harga. Ini berhasil 50 tahun yang lalu.
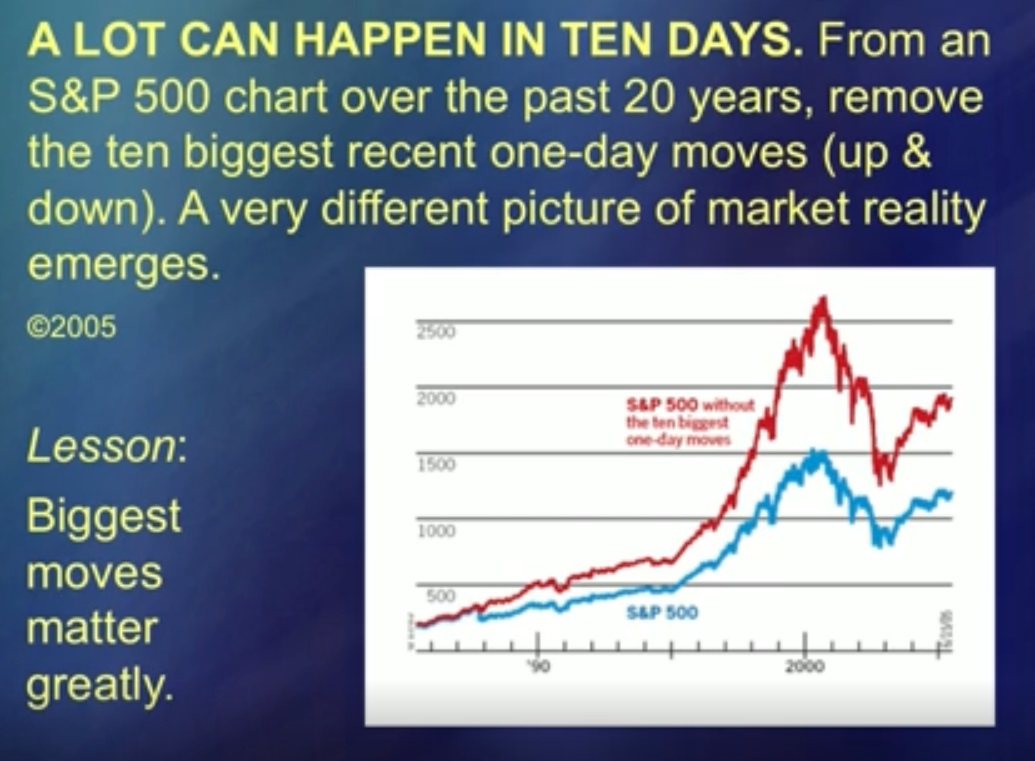
Selama 50 tahun, ide saya diejek karena bisa dilakukan dengan lebih mudah. Tetapi sekarang, saya katakan, mereka mulai mendengarkan saya. (Tawa) Kedua kurva ini mewakili rata-rata. Biru adalah Standard and Poor's [S&P 500] dan merah adalah Standard and Poor's, dari mana 5 lonjakan harga terbesar telah dikurangi. Lompatan itu tentu saja merusak analisis, dan dalam banyak penelitian itu dianggap [non-analitik] sebagai kasus khusus. “Kebetulan yang luar biasa, intervensi dari Tuhan. Nah, sedikit, Anda bisa mengesampingkannya. " Intervensi Tuhan pada grafik ini, dan ternyata ada lima, yang sama pentingnya dengan yang lainnya. Dengan kata lain, intervensi Tuhan tidak dapat diabaikan.
Itu adalah makhluk, itu adalah objek analisis. Jika Anda berurusan dengan mereka, Anda juga bisa berurusan dengan pergerakan harga. Tapi saya belum menemukan lompatannya, maka Anda dapat menganalisis apa yang disebut kebisingan sebanyak yang Anda suka, tetapi analisis ini tidak masuk akal. Kurva ini menunjukkan dampaknya.

Sekarang saya akan beralih ke topik terakhir - set bernama setelah saya. Di satu sisi, ini adalah kisah hidup saya. Masa remaja saya dihabiskan di Perancis, yang diduduki oleh Jerman pada tahun-tahun itu. Karena saya pikir kapan saja saya mungkin tidak, saya punya mimpi besar. Setelah perang, saya bertemu paman saya lagi. Paman saya adalah ahli matematika yang luar biasa dan dia berkata, “Ini masalah untuk Anda. 25 tahun yang lalu saya tidak bisa menyelesaikannya, dan tidak ada yang bisa menyelesaikannya. Ini adalah konstruksi dari satu ahli matematika bernama Gaston Julia dan yang lainnya bernama Pierre Fatou. Jika Anda dapat menemukan sesuatu yang baru di sini - apa pun - pertimbangkan karier Anda terjamin. " Sangat sederhana. Saya mulai mempelajari masalah ini, dan, seperti ribuan orang yang mencoba melakukannya sebelum saya, tidak berhasil.
Tapi kemudian komputer datang. Dan saya memutuskan bahwa saya perlu menerapkan daya komputasi bukan untuk masalah matematika baru - seperti, misalnya, hal melengkung ini: ini adalah masalah baru - tetapi untuk masalah lama. Dan saya beralih dari apa yang disebut bilangan real, yaitu dari titik pada garis lurus ke bilangan kompleks, dan ini adalah titik pada bidang, yaitu, apa yang diperlukan dalam masalah ini. Hasilnya adalah angka seperti itu.

Ini adalah kompleksitas yang luar biasa. Persamaannya tersembunyi di dalamnya: z berubah menjadi z ^ 2 + c. Sangat sederhana dan membosankan, sangat tidak menarik. Sekarang mari kita jalankan sekali, dua kali ... Dua kali sudah cukup. Tentang keajaiban! Inilah yang muncul. Saya tidak akan menjelaskan hal-hal ini di sini, tetapi ternyata ini adalah apa dan ini adalah apa.


Sosok kompleksitas seperti itu, harmoni dan keindahan seperti itu diperoleh berulang kali, berulang-ulang. Penemuan utama saya adalah bahwa pulau-pulau ini memiliki bentuk yang sama, kurang lebih, seperti keseluruhan gambar. Hasilnya adalah perhiasan barok yang memukau.

Dan semua formula pendek ini, di mana ada segalanya - ada berapa? - lima ikon. Dan inilah hasilnya.

Warna ditambahkan karena dua alasan. Pertama, karena angka-angka itu sangat kompleks sehingga sulit untuk melihat apa arti angka-angka itu. Dan Anda perlu memilih semacam sistem untuk mencerminkan mereka di pesawat. Oleh karena itu, saya menganggapnya sebagai prinsip untuk selalu mewakili angka dalam warna berbeda: satu warna berarti satu hal, dan yang lain berarti yang lain, dll. Ini sangat sulit.
Pada tahun 1990, saya berada di Inggris, di Cambridge, di mana saya dianugerahi hadiah dari universitas. Tiga hari kemudian, seorang pilot, terbang di atas lapangan, melihat ini.

Dari mana datangnya hal seperti itu? Tentu saja - dari alien.
Salah satu surat kabar di Cambridge menerbitkan sebuah artikel tentang "penemuan" ini, dan hari berikutnya menerima 5 ribu surat, yang mengatakan bahwa ini adalah set Mandelbrot, hanya sangat besar.

Biarkan saya selesai. Gambar ini diperoleh melalui matematika murni. Aturan sederhana bisa menciptakan keajaiban tanpa dasar jika diulang tanpa henti.
Diterjemahkan oleh Namik Kasumov
Diulas oleh Ekaterina Tsvetkova

Pelajari detail cara mendapatkan profesi yang dicari dari awal atau Tingkatkan keterampilan dan gaji dengan menyelesaikan kursus online berbayar SkillFactory:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- Data Science
- Data Science : «data»
- Data Sciene : Decision Intelligence