Kami memahami dan menciptakan
Kabar baik sebelum artikel: keterampilan matematika tinggi tidak diperlukan untuk membaca dan (semoga!) Pemahaman.
Penafian: bagian kode artikel ini, seperti yang sebelumnya , adalah terjemahan yang diadaptasi, ditambah, dan diuji. Saya berterima kasih kepada penulis, karena ini adalah salah satu pengalaman pertama saya dalam kode, setelah itu saya membanjiri lebih banyak lagi. Saya harap adaptasi saya akan bekerja sama untuk Anda!
Jadi ayo pergi!
Strukturnya seperti ini:
- Apa itu rantai Markov?
- Contoh cara kerja rantai
- Matriks transisi
- Model rantai Markov dengan Python - pembuatan teks berbasis data
Apa itu rantai Markov?
Rantai markov adalah alat dari teori proses acak, terdiri dari urutan n jumlah keadaan. Dalam hal ini, koneksi antara node (nilai) dari rantai dibuat hanya jika statusnya berdekatan satu sama lain.
Dengan mengingat kata tipe lemak saja , mari kita simpulkan sifat rantai Markov:
Probabilitas keadaan baru tertentu dalam rantai hanya bergantung pada keadaan saat ini dan tidak secara matematis memperhitungkan pengalaman keadaan masa lalu => Rantai Markov adalah rantai tanpa memori.
Dengan kata lain, makna baru selalu menari dari makna yang dipegang langsung pada pegangannya.
Contoh cara kerja rantai
Seperti penulis artikel tempat implementasi kode dipinjam, mari kita ambil urutan kata acak.
Start - tiruan - mantel bulu - tiruan - makanan - tiruan - pasta - tiruan - mantel bulu - buatan - akhir
Mari kita bayangkan bahwa ini sebenarnya adalah ayat yang bagus dan tugas kita adalah meniru gaya penulisnya. (Tetapi melakukannya, tentu saja, tidak etis)
Bagaimana cara memutuskan?
Hal pertama yang jelas ingin saya lakukan adalah menghitung frekuensi kata (jika kita melakukan ini dengan teks langsung, pertama-tama akan bermanfaat untuk menormalkannya - untuk membawa setiap kata ke lemma (bentuk kamus)).
Start == 1
Artificial == 5
Fur coat == 2
Pasta == 1
Food == 1
End == 1
Mengingat bahwa kita memiliki rantai Markov, kita dapat memplot distribusi kata-kata baru tergantung pada kata-kata sebelumnya secara grafis:

Secara lisan:
- keadaan lapisan bulu, makanan dan pasta 100% memerlukan keadaan buatan p = 1
- keadaan "buatan" dapat menyebabkan 4 kondisi dengan probabilitas yang sama, dan probabilitas untuk mencapai kondisi mantel bulu buatan lebih tinggi daripada tiga kondisi lainnya
- keadaan akhir tidak mengarah ke mana pun
- negara bagian "mulai" 100% memerlukan negara bagian "buatan"
Ini terlihat keren dan logis, tetapi keindahan visual tidak berhenti di situ! Kita juga dapat membuat matriks transisi, dan atas dasarnya kita dapat mengajukan banding dengan keadilan matematis berikut:

Apa dalam bahasa Rusia berarti "jumlah rangkaian probabilitas untuk peristiwa tertentu k, bergantung pada i == jumlah semua nilai probabilitas peristiwa k, bergantung pada kemunculan keadaan i, di mana peristiwa k == m + 1, dan event i == m (yaitu, event k selalu berbeda satu dari i) ”.
Tapi pertama-tama, mari kita pahami apa itu matriks.
Matriks transisi
Saat bekerja dengan rantai Markov, kita berurusan dengan matriks transisi stokastik - sekumpulan vektor, di mana nilainya mencerminkan nilai probabilitas antara gradasi.
Ya, ya, kedengarannya seperti itu.
Tapi itu tidak terlihat terlalu menakutkan:

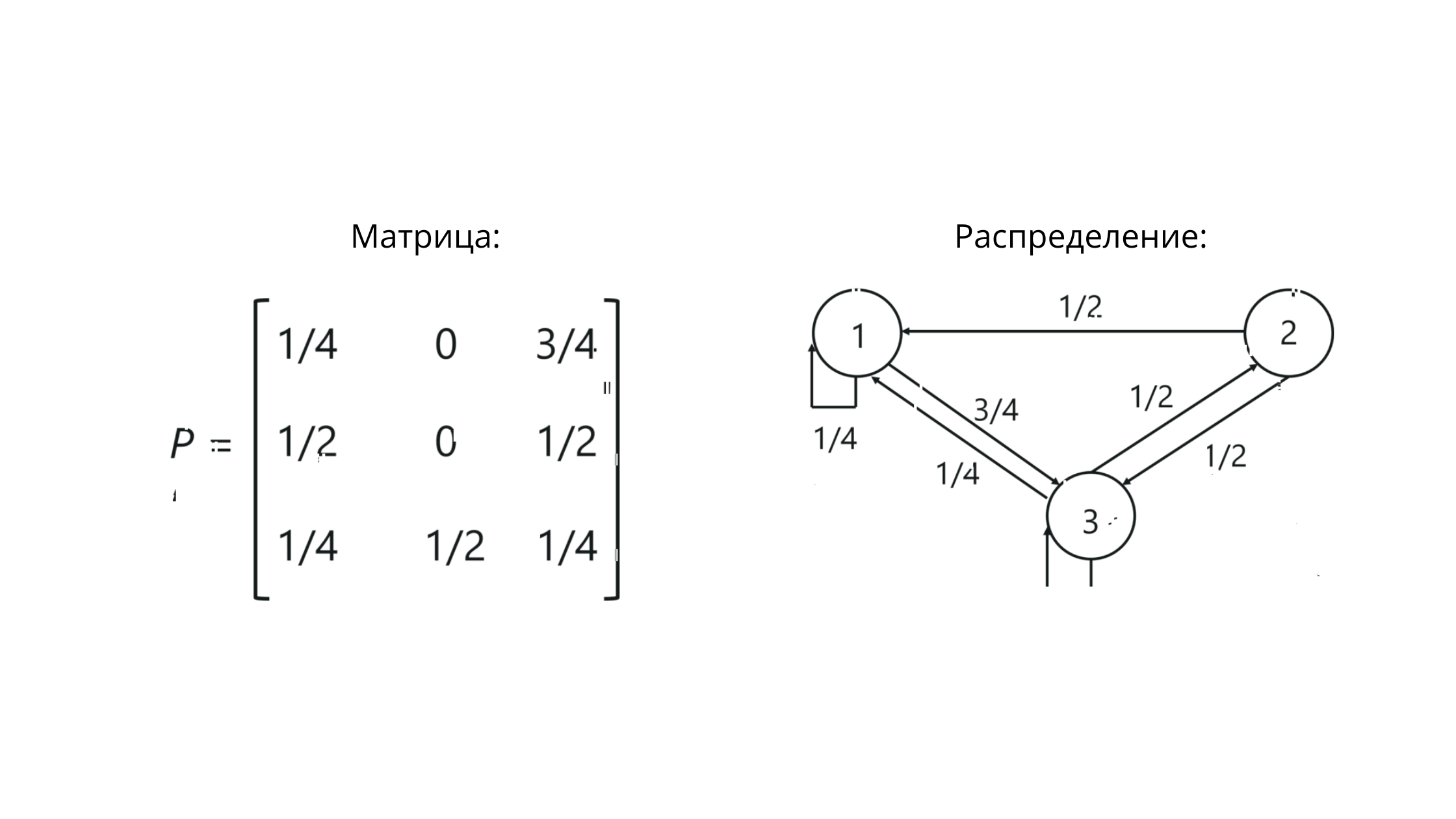
P adalah notasi untuk matriks. Nilai-nilai di persimpangan kolom dan baris di sini mencerminkan kemungkinan transisi antar negara bagian.
Untuk contoh kita, akan terlihat seperti ini:

Perhatikan bahwa jumlah nilai dalam baris == 1. Ini berarti kita telah membangun semuanya dengan benar, karena jumlah nilai dalam baris matriks stokastik harus sama dengan satu.
Contoh telanjang tanpa mantel dan pasta bulu palsu: Contoh
telanjang bulat adalah matriks identitas untuk:
- kasus ketika tidak mungkin untuk pergi dari A kembali ke B, dan dari B - kembali ke A [1]
- kasus ketika transisi dari A ke B kembali dimungkinkan [2]

Respecto. Dengan teori selesai.
Kami menggunakan Python.
Model berdasarkan rantai Markov menggunakan Python - menghasilkan teks berdasarkan data.
Langkah 1
Impor paket yang relevan untuk pekerjaan dan dapatkan datanya.
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
Jangan fokus pada struktur teks, tapi perhatikan encoding utf8. Ini penting untuk membaca data.
Langkah 2
Bagilah data menjadi kata-kata.
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']Langkah 3
Mari buat fungsi untuk menghubungkan pasangan kata.
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)Nuansa utama fungsi dalam penggunaan operator yield (). Ini membantu kami memenuhi kriteria rangkaian Markov - kriteria penyimpanan tanpa memori. Dengan hasil, fungsi kita akan membuat pasangan baru saat iterasi (pengulangan), daripada menyimpan semuanya.
Kesalahpahaman mungkin muncul di sini, karena satu kata bisa berubah menjadi kata yang berbeda. Kami akan menyelesaikan ini dengan membuat kamus untuk fungsi kami.
LANGKAH 4
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]Sini:
- Jika kita sudah memiliki entri tentang kata pertama dalam pasangan di kamus, fungsi menambahkan nilai potensial berikutnya ke daftar.
- jika tidak: entri baru dibuat.
Langkah 5
Mari kita pilih kata pertama secara acak dan, untuk membuat kata benar-benar acak, setel kondisi while menggunakan metode string islower (), yang memenuhi True jika string berisi huruf kecil, memungkinkan adanya angka atau simbol.
Dalam kasus ini, setel jumlah kata menjadi 20.
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))Langkah 6
Mari kita mulai hal acak kita!
print(' '.join(chain))
; .., , , (Fungsi join () adalah fungsi untuk bekerja dengan string. Dalam tanda kurung, kami telah menentukan pemisah untuk nilai-nilai di baris (spasi).
Dan teksnya ... yah, kedengarannya seperti mesin dan hampir logis.
PS Seperti yang mungkin telah Anda ketahui, rantai Markov berguna dalam linguistik, tetapi aplikasinya melampaui pemrosesan bahasa alami. Di sini dan di sini Anda dapat membiasakan diri dengan penggunaan rantai dalam tugas lain.
PPS Jika praktik kode saya ternyata tidak dapat dipahami oleh Anda, saya melampirkan artikel asli . Pastikan untuk menerapkan kode dalam praktik - perasaan saat kode "dijalankan dan dihasilkan" sedang mengisi daya!
Saya menunggu pendapat Anda dan saya akan senang memberikan komentar yang membangun untuk artikel ini!