🏟️ ☝🏽 🔘 Jaringan Bayesian dengan Python - apa dan mengapa? 🥛 🛤️ 🎅🏻

Penafian: Artikel ini adalah terjemahan yang disesuaikan. Yang asli bisa dibaca di sini .

Bayesian Networks dengan Python - Dijelaskan dengan Contoh

Karena informasi yang terbatas (terutama dalam bahasa Rusia asli) dan sumber daya kerja, jaringan Bayesian dikelilingi oleh sejumlah masalah. Dan orang bisa tidur nyenyak jika tidak diimplementasikan di sebagian besar teknologi canggih pada zaman itu, seperti kecerdasan buatan dan pembelajaran mesin.

Berdasarkan fakta ini, artikel ini sepenuhnya dikhususkan untuk karya jaringan Bayesian dan bagaimana mereka sendiri tidak dapat membentuk masalah, tetapi diterapkan dalam menyelesaikannya, bahkan jika masalah yang diselesaikan sangat membingungkan.

Struktur artikel

Apa itu Jaringan Bayesian?
Apa itu grafik asiklik terarah?
Apa matematika terletak di jaringan Bayesian
Contoh yang mencerminkan gagasan jaringan Bayesian
Esensi dari jaringan Bayesian
Jaringan Bayesian dengan Python
Penerapan jaringan Bayesian

Ayo pergi.

Apa itu Jaringan Bayesian?

Jaringan Bayesian termasuk dalam kategori model grafis probabilistik (GPM). VGM digunakan untuk menghitung variabilitas untuk aplikasi dalam konsep probabilitas.

Nama umum untuk jaringan Bayesian adalah Deep Networks. Mereka digunakan untuk memodelkan grafik asiklik terarah.

Apa itu grafik asiklik terarah?

Grafik asiklik terarah (seperti grafik apa pun dalam statistik) adalah struktur simpul dan tautan, di mana simpul bertanggung jawab atas beberapa nilai, dan tautan mencerminkan hubungan antar simpul.

Acyclic == tidak memiliki siklus terarah. Dalam konteks grafik, kata sifat ini berarti memulai jalur dari satu titik, kita tidak melalui seluruh diagram grafik, tetapi hanya sebagian saja. (Yaitu, misalnya, jika kita mulai dari simpul 2 dalam gambar, kita pasti tidak akan sampai ke simpul 1).

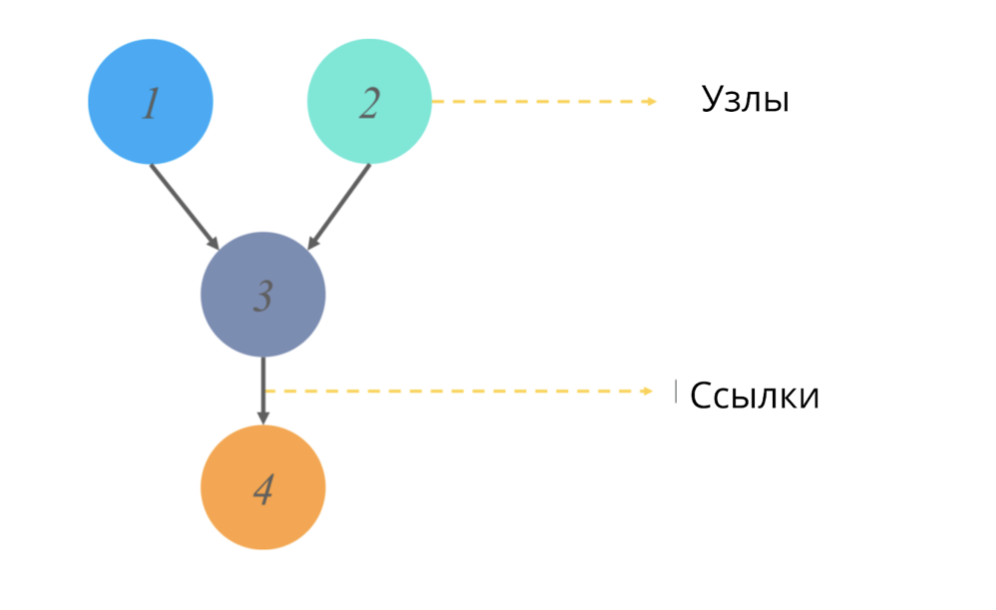
Apa yang disimulasikan grafik ini dan apa nilai output yang mereka berikan?

Model grafik terarah yang tidak pasti juga didasarkan pada perubahan dalam asal usul probabilistik suatu kejadian untuk masing-masing nilai acak. Tabel probabilitas bersyarat berlaku untuk mewakili dan menafsirkan setiap nilai dan dengan demikian kita dapat mensimulasikan percabangan probabilitas peristiwa berurutan.

Semua baik-baik saja Saya juga bingung pada awalnya. Untuk pemahaman yang lebih baik, mari kita menganalisis komponen matematika dari jaringan Bayesian.

Matematika Jaringan Bayesian

Seperti yang telah disebutkan dalam definisi, Bayesian Networks didasarkan pada teori probabilitas, oleh karena itu, sebelum mulai bekerja dengan jaringan Bayesian, dua pertanyaan harus ditangani:

Apa itu probabilitas bersyarat?

Apa distribusi probabilitas rata-rata gabungan?

Peluang

bersyarat Peluang bersyarat dari beberapa peristiwa X adalah nilai numerik dari probabilitas bahwa peristiwa X akan terjadi, asalkan beberapa peristiwa Y telah terjadi.

Rumus probabilitas standar untuk satu nilai (tidak diberikan dalam artikel): P (X) = n (x) / N, di mana n adalah peristiwa yang sedang diselidiki, dan N adalah semua peristiwa yang mungkin.

Untuk dua nilai, rumus berikut ini berlaku:

Jika X dan Y adalah peristiwa yang bergantung:

P (X atau Y) = P (X ⋂ Y) / P (Y), persimpangan probabilitas X dan Y / pada probabilitas Y. (Tanda "" dalam pembilang berarti persimpangan probabilitas)

Jika peristiwa X dan Y adalah independen:

P (X) atau Y) = P (X), yaitu, kejadian peristiwa yang diteliti kemungkinan sama besar satu sama lain.

Probabilitas gabungan Probabilitas

gabungan adalah definisi ukuran statistik untuk dua atau lebih peristiwa yang terjadi pada saat yang sama. Yaitu, peristiwa X, Y dan, katakanlah C terjadi bersama-sama dan kami mencerminkan probabilitas kumulatif mereka menggunakan nilai P (X ⋂ Y ⋂ C).

Bagaimana cara kerjanya di jaringan Bayesian? Mari kita lihat sebuah contoh.

Sebuah contoh yang mencerminkan esensi dari jaringan Bayesian

Katakanlah kita perlu memodelkan kemungkinan mendapatkan salah satu nilai dari nilai siswa pada ujian.

Skor terdiri dari:

Tingkat kesulitan ujian (e): variabel diskrit dengan dua gradasi (sulit, mudah)
Student IQ: variabel diskrit dengan dua gradasi (rendah, tinggi)

Nilai penilaian yang dihasilkan akan digunakan sebagai prediktor (nilai prediktif) dari kemungkinan seorang siswa atau siswa perempuan memasuki universitas.

Namun, variabel IQ juga akan memengaruhi penerimaan masuk.

Kami mewakili semua nilai menggunakan grafik asiklik terarah dan tabel distribusi probabilitas bersyarat.

Dengan menggunakan representasi ini, kita dapat menghitung beberapa probabilitas kumulatif, terbentuk dari produk dari probabilitas bersyarat dari lima variabel.

Peluang kumulatif:

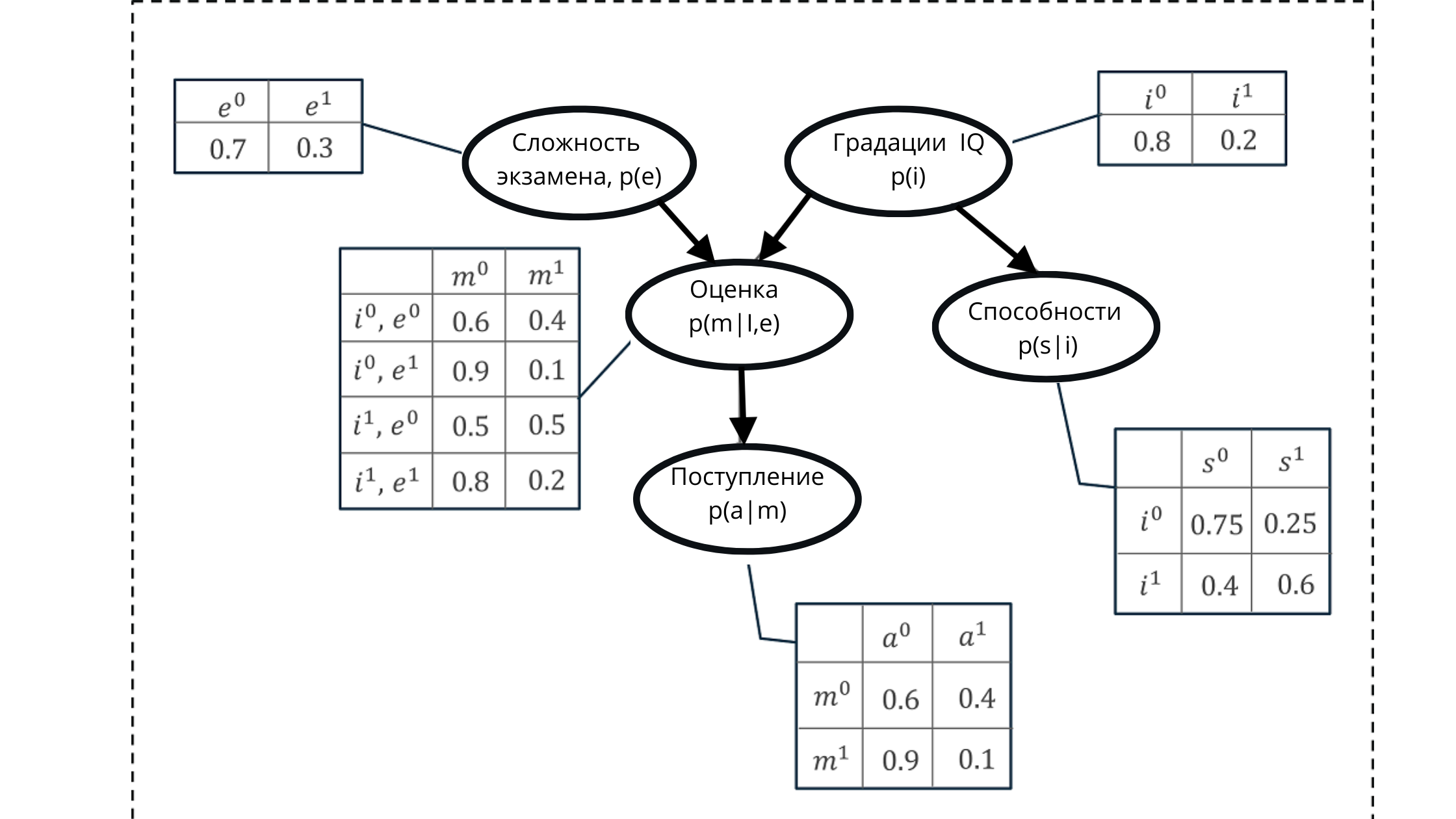
p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e) p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e)

$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$

Dalam ilustrasi:

p (e) adalah distribusi probabilitas untuk nilai-nilai variabel ujian (mempengaruhi nilai p (m | i, e)))

p (i) adalah distribusi probabilitas untuk nilai-nilai variabel IQ (mempengaruhi nilai p (m | i, e )))

p (m | i, e) - distribusi probabilitas untuk nilai kelas, berdasarkan tingkat IQ dan kesulitan ujian (tergantung pada p (i) dan p (e))

p (s | i) - koefisien probabilitas untuk kemampuan siswa , berdasarkan tingkat IQ-nya (tergantung pada variabel IQ p (i))

p (a | m) adalah probabilitas pendaftaran siswa di universitas, berdasarkan perkiraannya p (m | i, e)

Di sini, izinkan saya mengingatkan Anda bahwa properti grafik asiklik adalah refleksi hubungan. Dalam gambar, kita dapat dengan jelas melihat bagaimana simpul orang tua mempengaruhi anak-anak dan bagaimana anak-anak bergantung pada orang tua.

Oleh karena itu formulasi set nilai yang dihasilkan menggunakan jaringan Bayesian muncul.

Inti dari Jaringan Bayesian

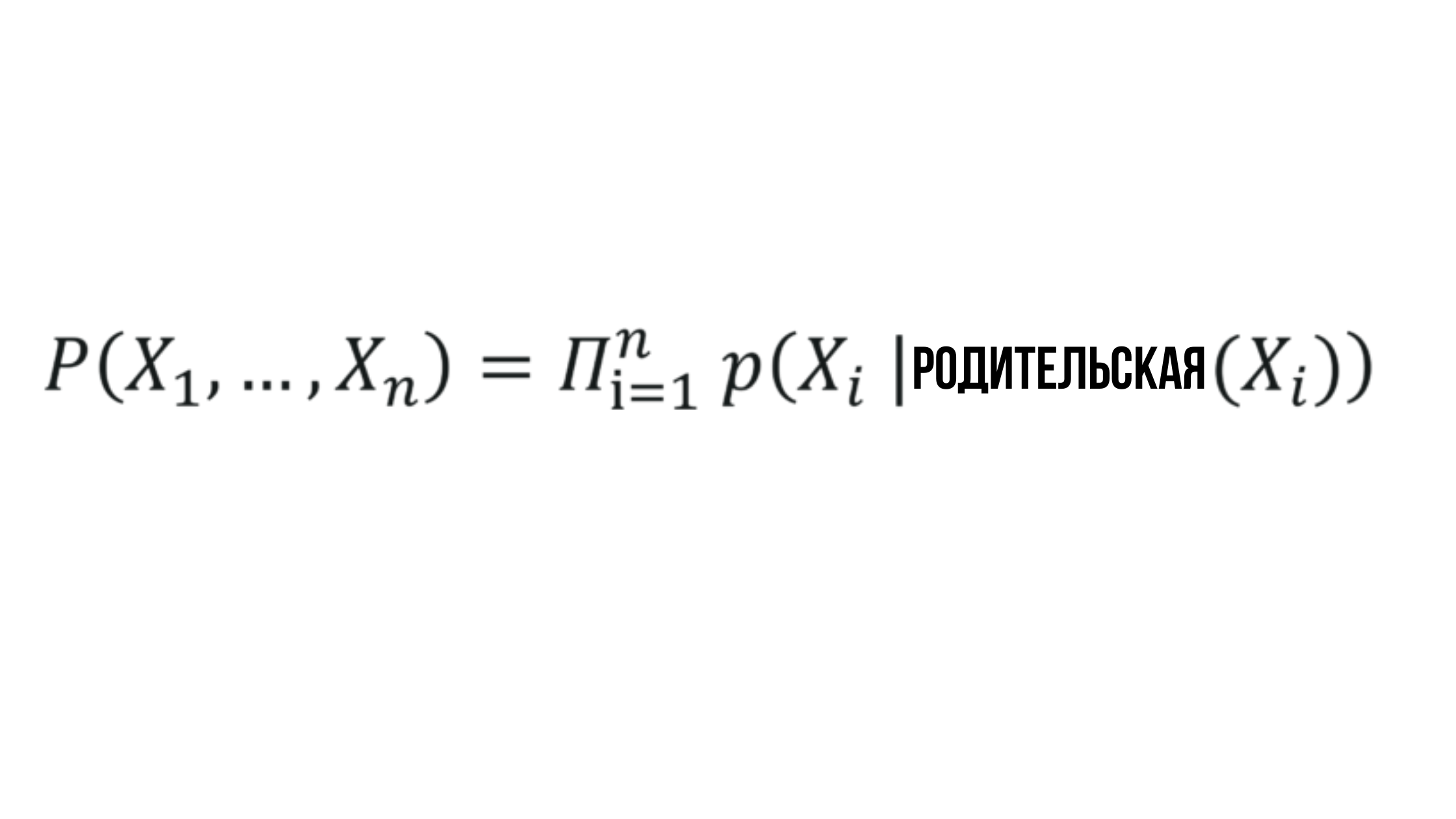
Dimana probabilitas X_i tergantung pada probabilitas simpul induk yang sesuai dan dapat diwakili oleh nilai acak apa pun.

Kedengarannya sederhana, dan memang seharusnya begitu - jaringan Bayesian adalah salah satu metode paling sederhana yang digunakan dalam analisis deskriptif, pemodelan prediktif, dan banyak lagi.

Jaringan Bayesian dengan Python

Mari kita lihat menerapkan jaringan Bayesian ke masalah yang disebut paradoks Monty Hall.

Intinya: Bayangkan Anda adalah peserta dalam format pembaruan game "Field of Miracles". Drum tidak lagi berputar - sekarang Anda seharusnya tidak menerapkan F Anda, tetapi bermain dengan hal.

Ada tiga pintu di depan Anda, di belakangnya ada satu mobil yang sama-sama terletak. Pintu-pintu, di belakangnya tidak ada mobil, akan membawa Anda ke kambing.

Setelah memilih, pemimpin yang tersisa membuka yang mengarah ke kambing (misalnya, Anda memilih pintu 1, yang berarti bahwa pemimpin membuka pintu 2 atau 3) dan mengundang Anda untuk mengubah pilihan Anda.

Pertanyaan: apa yang harus dilakukan?

Solusi: awalnya probabilitas memilih pintu dengan mobil = 33%, dan dengan kambing = 66%.

Jika Anda menekan 33%, mengubah pintu menyebabkan kerugian => peluang menang == 33%
Jika Anda menekan 66% perubahan menyebabkan kemenangan => probabilitas menang == 66%

Dari sudut pandang logika matematika, mengubah pintu secara agregat mengarah pada kemenangan di 66% persen, dan kerugian di 33%. Karena itu, strategi yang tepat adalah mengubah pintu.

Tapi kita berbicara tentang jaringan di sini, dan mungkin ada banyak pintu, jadi kami akan mentransfer solusi ke model.

Mari kita buat grafik asiklik terarah dengan tiga simpul:

Pintu hadiah (selalu dengan mobil)
Pintu yang dapat dipilih (baik dengan mobil atau dengan kambing)
Pintu yang dapat dibuka di acara 1 (selalu dengan kambing)

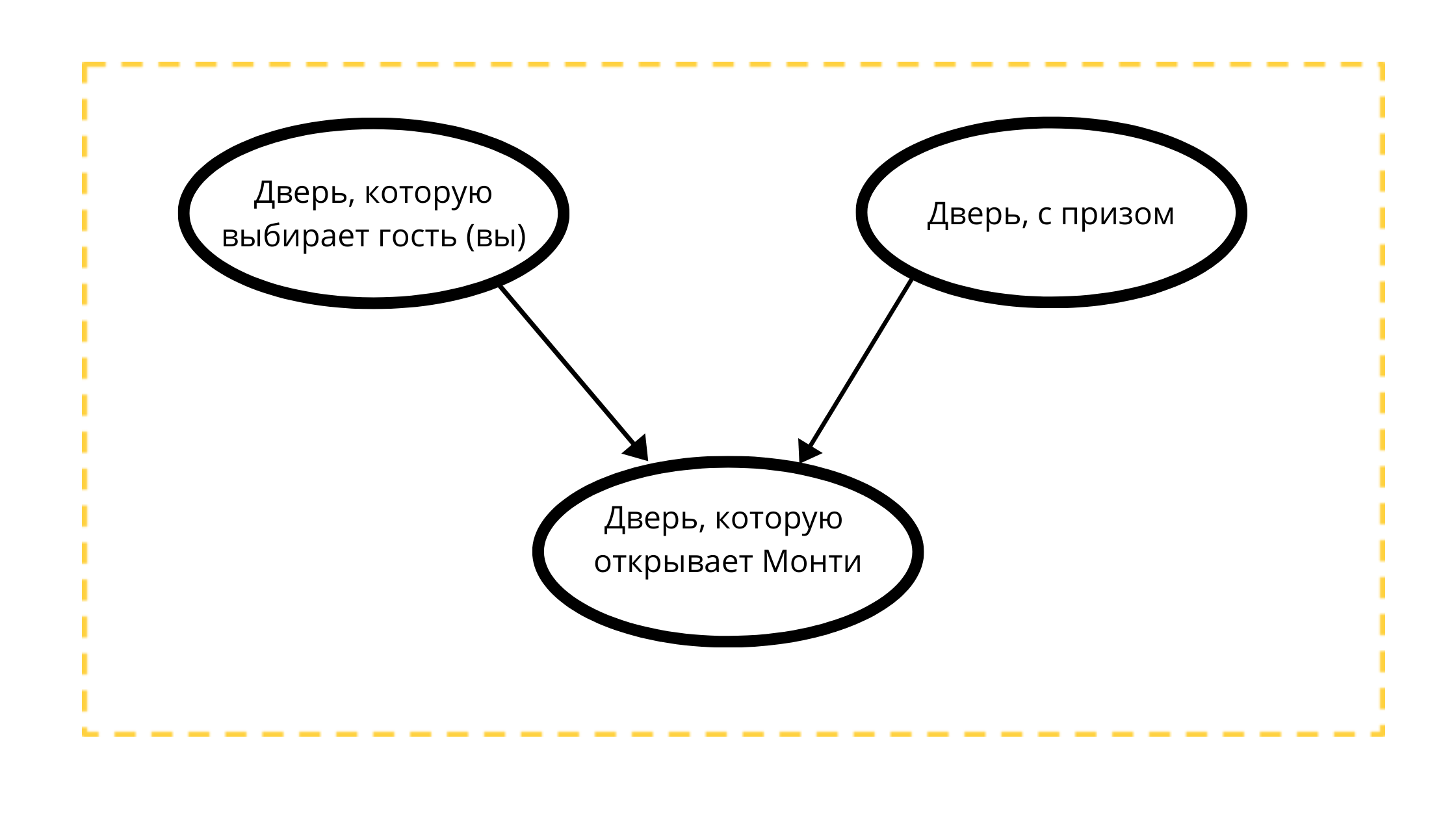
Membaca Hitungan:

Pintu yang Monty akan buka sangat dipengaruhi oleh dua variabel:

Pintu yang dipilih oleh tamu (Anda) tk Monti 100% TIDAK akan membuka pilihan Anda
Sebuah pintu dengan hadiah, mungkin Monty selalu membuka pintu tanpa hadiah.

Menurut kondisi matematika dari contoh klasik, hadiah dapat ditempatkan di belakang pintu, seperti halnya Anda dapat memilih pintu mana pun.

#   
import math
from pomegranate import *
 
#    "  " (   3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#    "   " (    )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#  ,       ,     
#    
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#  
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

Dalam cuplikan, nilainya adalah:

A - pintu yang dipilih oleh tamu
Pintu B-hadiah
Pintu-C dipilih oleh Monty

Pada fragmen, kami menghitung nilai probabilitas untuk masing-masing node dari grafik. Dua node teratas mematuhi dalam contoh kami distribusi probabilitas yang sama, dan yang ketiga mencerminkan distribusi dependen. Oleh karena itu, agar tidak kehilangan nilai, probabilitas masing-masing kemungkinan kombinasi permainan dihitung untuk .

Setelah menyiapkan data, kami membuat jaringan Bayesian.

Penting untuk dicatat di sini bahwa salah satu sifat dari jaringan semacam itu adalah untuk mengungkapkan pengaruh variabel tersembunyi pada yang dapat diamati. Pada saat yang sama, baik variabel tersembunyi maupun yang dapat diamati tidak perlu ditentukan atau ditentukan sebelumnya - model itu sendiri memeriksa pengaruh variabel tersembunyi dan akan melakukan ini dengan lebih akurat, semakin banyak variabel yang diterimanya.

Mari mulai membuat prediksi.

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

Mari kita menganalisis fragmen menggunakan contoh variabel A.

Misalkan tamu memilihnya (A).

Acara "ada hadiah di balik pintu" pada tahap memilih pintu oleh tamu memiliki distribusi probabilitas == ⅓ (karena setiap pintu mungkin sama-sama menjadi hadiah).

Selanjutnya, tambahkan nilai probabilitas pintu menjadi hadiah di panggung saat pintu dipilih oleh Monty. Karena kita tidak tahu apakah pintu hadiah dikecualikan oleh pilihan (tamu) kita sendiri pada langkah 1, probabilitas pintu menjadi hadiah pada tahap ini adalah 50/50

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

Pada langkah ini, kami akan memodifikasi nilai input untuk jaringan kami. Sekarang berfungsi dengan distribusi probabilitas yang diperoleh pada langkah 1 dan 2, di mana

peluang menang di depan pintu pilihan kami tidak berubah (33%)
peluang memenangkan hadiah di pintu yang dibuka oleh Monty (B) telah dibatalkan
peluang menjadi hadiah di pintu, yang dibiarkan tanpa pengawasan, mengambil nilai 66%

Oleh karena itu, seperti yang telah disimpulkan di atas, strategi yang tepat di pihak para tamu untuk permainan ini adalah mengubah pintu - mereka yang mengubah pintu secara matematis memiliki ⅔ peluang menang melawan mereka yang tidak akan mengubah pintu (⅓).

Dalam contoh dengan tiga node, perhitungan manual tidak diragukan lagi cukup, tetapi dengan peningkatan jumlah variabel, node dan faktor yang mempengaruhi, jaringan Bayesian mampu memecahkan masalah nilai prediktif.

Penerapan jaringan Bayesian

1. Diagnostik:

prediksi penyakit berdasarkan gejala
pemodelan gejala untuk penyakit yang mendasarinya

2. Mencari di Internet:

pembentukan hasil pencarian berdasarkan analisis konteks pengguna (niat)

3. Klasifikasi dokumen:

filter spam berdasarkan analisis konteks
distribusi dokumentasi berdasarkan kategori / kelas

4. Rekayasa genetika

memodelkan perilaku jaringan regulasi gen berdasarkan interkoneksi dan hubungan segmen DNA

5. Farmasi:

pemantauan dan nilai prediksi dosis yang dapat diterima

Contoh di atas adalah fakta. Untuk pemahaman yang lengkap, adalah relevan untuk membayangkan pada tahap apa penciptaan jaringan Bayesian terhubung dan simpul-simpul yang menggambarkan grafik yang terdiri darinya.

Masalah paradoks Monty Hall hanyalah sebuah yayasan yang memungkinkan seseorang untuk "ujung jari" menggambarkan operasi rantai berdasarkan pada kombinasi distribusi probabilitas dependen dan independen. Saya harap saya mengerti.

PS Saya bukan kartu As Python dan hanya belajar, jadi saya tidak dapat bertanggung jawab atas kode penulis. Publikasi artikel ini tentang Habré mengejar lebih banyak rilis ke dunia karya intelektual terjemahan. Saya pikir di masa depan saya akan dapat menghasilkan tutorial saya sendiri - di dalamnya saya sudah akan senang melihat pemikiran konstruktif tentang kode.

Jaringan Bayesian dengan Python - apa dan mengapa?