di mana q adalah muatan partikel, r ij adalah jarak antar partikel, C adalah beberapa konstanta tergantung pada pilihan satuan pengukuran. Dalam SI itu adalah -, dalam SGS - 1, dalam program saya (di mana energi dinyatakan dalam volt elektron, jarak dalam angstrom, dan muatan dalam muatan dasar) C kira-kira sama dengan 14,3996.
Jadi apa katamu? Cukup tambahkan istilah yang sesuai untuk potensi pasangan dan Anda selesai. Namun, paling sering dalam pemodelan MD, kondisi batas periodik digunakan, yaitu sistem simulasi dikelilingi dari semua sisi dengan jumlah tak terbatas dari salinan virtualnya. Dalam hal ini, setiap gambar virtual dari sistem kami akan berinteraksi dengan semua partikel bermuatan di dalam sistem sesuai dengan hukum Coulomb. Dan karena interaksi Coulomb menurun sangat lemah dengan jarak (seperti 1 / r), tidak mudah untuk mengabaikannya, dengan mengatakan bahwa kita tidak menghitungnya dari jarak ini dan itu. Serangkaian bentuk 1 / x diverges, mis. jumlahnya, pada prinsipnya, dapat tumbuh tanpa batas. Dan sekarang, tidakkah Anda memberi garam pada semangkuk sup? Apakah itu akan membunuhmu dengan listrik?
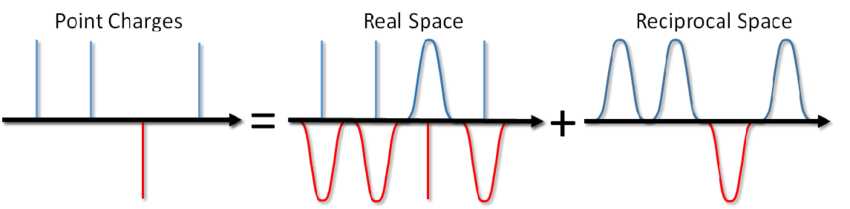
... Anda tidak hanya dapat garam sup, tetapi juga menghitung energi dari interaksi Coulomb dalam kondisi batas periodik. Metode ini diusulkan oleh Ewald pada tahun 1921 untuk menghitung energi kristal ionik (Anda juga dapat melihatnya di Wikipedia ). Inti dari metode ini adalah untuk menyaring muatan titik dan kemudian mengurangi fungsi penyaringan. Dalam hal ini, bagian dari interaksi elektrostatik direduksi menjadi aksi pendek dan dapat dengan mudah dipotong dengan cara standar. Bagian jarak jauh yang tersisa secara efektif dijumlahkan dalam ruang Fourier. Dengan mengabaikan kesimpulan, yang dapat dilihat dalam artikel Blinov atau dalam buku yang sama oleh Frenkel dan Smith , saya akan segera menuliskan solusi yang disebut jumlah Ewald:
di mana α adalah parameter yang mengatur rasio perhitungan dalam ruang maju dan mundur, k adalah vektor dalam ruang timbal balik di mana penjumlahan berlangsung, V adalah volume sistem (dalam ruang maju). Bagian pertama (E real ) adalah jarak pendek dan dihitung dalam siklus yang sama dengan potensi pasangan lainnya, lihat fungsi real_ewald di artikel sebelumnya. Kontribusi terakhir ( Econst ) adalah koreksi untuk interaksi diri dan sering disebut "bagian konstan" karena tidak tergantung pada koordinat partikel. Perhitungannya sepele, jadi kami hanya akan fokus pada bagian kedua dari jumlah Ewald (E rec), penjumlahan dalam ruang timbal balik. Secara alami, pada saat derivasi Ewald, tidak ada dinamika molekuler, saya tidak dapat menemukan siapa yang pertama kali menggunakan metode ini dalam MD. Saat ini, setiap buku tentang MD mengandung presentasinya sebagai semacam standar emas. Untuk memesan, Allen bahkan memberikan kode contoh di Fortran. Untungnya, saya masih memiliki kode yang pernah ditulis dalam C untuk versi sekuensial, tetap hanya untuk memparalelasinya (saya membiarkan diri saya menghilangkan beberapa deklarasi variabel dan detail tidak penting lainnya):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
Beberapa penjelasan untuk kode: fungsi menghitung eksponen kompleks (dalam komentar dengan kode itu dilambangkan iexp untuk menghapus unit imajiner dari kurung) dari produk vektor k-vektor dan vektor jari-jari partikel untuk semua vektor-k dan untuk semua partikel. Eksponen ini dikalikan dengan muatan partikel. Selanjutnya, jumlah produk tersebut untuk semua partikel dihitung (jumlah internal dalam rumus untuk E rec ), dalam Frenkel disebut kepadatan muatan, dan dalam Blinov disebut faktor struktural. Dan kemudian, berdasarkan faktor-faktor struktural ini, energi dan gaya yang bekerja pada partikel dihitung. Komponen k-vektor (2π * l / a, 2π * m / b, 2π * n / c) dikarakterisasi oleh tiga bilangan bulat l , m dan n, yang berjalan dalam siklus hingga batas yang ditentukan pengguna. Parameter a, b dan c adalah dimensi dari sistem yang disimulasikan dalam dimensi x, y dan z, masing-masing (kesimpulannya benar untuk sistem dengan geometri parallelepiped persegi panjang). Dalam kode, 1 / a , 1 / b, dan 1 / c sesuai dengan variabel ra , rb, dan rc . Array untuk setiap nilai disajikan dalam dua salinan: untuk bagian nyata dan imajiner. Setiap k-vektor berikutnya dalam satu dimensi diperoleh secara iteratif dari yang sebelumnya dengan mengalikan kompleks sebelumnya dengan satu, sehingga tidak menghitung sinus dengan cosinus setiap kali. Array emc / s dan enc / s diisi untuk semua mdan n , masing-masing, dan array elc / s menempatkan nilai untuk setiap l > 1 dalam indeks nol l untuk menghemat memori.
Untuk tujuan paralelisasi, adalah menguntungkan untuk "membalikkan" urutan siklus sehingga siklus luar berjalan di atas partikel. Dan di sini kita melihat masalah - fungsi ini dapat diparalelkan hanya sebelum menghitung jumlah seluruh partikel (densitas muatan). Perhitungan lebih lanjut didasarkan pada jumlah ini, dan itu akan dihitung hanya ketika semua utas menyelesaikan pekerjaan mereka, jadi Anda harus membagi fungsi ini menjadi dua. Yang pertama menghitung kepadatan muatan, dan yang kedua menghitung energi dan gaya. Perhatikan bahwa fungsi kedua akan lagi membutuhkan kuantitas q iiexp (kr) untuk setiap partikel dan untuk masing-masing vektor-k, dihitung pada langkah sebelumnya. Dan di sini ada dua pendekatan: hitung ulang itu lagi, atau ingatlah.
Opsi pertama membutuhkan lebih banyak waktu, yang kedua - lebih banyak memori (jumlah partikel * jumlah k-vektor * sizeof (float2)). Saya memilih opsi kedua:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
Saya harap Anda memaafkan saya karena meninggalkan komentar dalam bahasa Inggris, kode ini praktis sama dengan versi serial. Kode bahkan menjadi lebih mudah dibaca karena fakta bahwa array kehilangan satu dimensi: elc / s [i] [l] , emc / s [i] [m] dan enc / s [i] [n] berubah menjadi el satu dimensi , em dan en , array lmc / s dan ckc / s - ke dalam variabel lm dan ck (dimensi oleh partikel telah menghilang, karena tidak ada lagi kebutuhan untuk menyimpannya untuk setiap partikel, hasil antara diakumulasikan dalam memori bersama). Sayangnya, masalah segera muncul: array em dan enharus disetel statis agar tidak menggunakan memori global dan tidak mengalokasikan memori secara dinamis setiap kali. Jumlah elemen di dalamnya ditentukan oleh direktif NKVEC_MX (jumlah maksimum vektor k dalam satu dimensi) pada tahap kompilasi, dan hanya elemen nky / z pertama yang digunakan saat runtime. Selain itu, indeks ujung ke ujung pada semua vektor k dan arahan yang serupa muncul, membatasi jumlah total vektor ini NTOTKVEC . Masalah akan muncul jika pengguna membutuhkan lebih banyak k-vektor daripada yang ditentukan oleh arahan. Untuk menghitung energi, sebuah blok dengan indeks nol disediakan, karena tidak masalah blok mana yang akan melakukan perhitungan ini dan dalam urutan apa. Perhatikan bahwa nilai dihitung dalam variabel akkkode serial hanya tergantung pada ukuran sistem yang disimulasikan dan dapat dihitung pada tahap inisialisasi, dalam implementasi saya disimpan dalam array md-> exprk2 [] untuk setiap k-vektor. Demikian pula, komponen vektor k diambil dari array md-> rk [] . Di sini mungkin perlu untuk menggunakan fungsi FFT yang sudah jadi, karena metode ini didasarkan pada itu, tapi saya masih tidak tahu bagaimana melakukannya.
Nah, sekarang mari kita coba menghitung sesuatu, tetapi natrium klorida yang sama. Mari kita ambil 2 ribu ion natrium dan jumlah klorin yang sama. Mari kita menetapkan biaya sebagai bilangan bulat, dan mengambil potensi pasangan, misalnya, dari pekerjaan ini... Mari kita atur konfigurasi awal secara acak dan campur sedikit, Gambar 2a. Kami memilih volume sistem sehingga sesuai dengan kepadatan natrium klorida pada suhu kamar (2,165 g / cm 3 ). Mari kita mulai semua ini untuk waktu yang singkat (10'000 langkah 5 femtoseconds) dengan pertimbangan elektrostatik yang naif menurut hukum Coulomb dan menggunakan penjumlahan Ewald. Konfigurasi yang dihasilkan masing-masing ditunjukkan pada Gambar 2b dan 2c. Tampaknya dalam kasus Ewald, sistemnya sedikit lebih ramping daripada tanpa dirinya. Penting juga bahwa fluktuasi energi total telah berkurang secara signifikan dengan penggunaan penjumlahan.

Gambar 2. Konfigurasi awal sistem NaCl (a) dan setelah 10'000 langkah integrasi: metode naif (b) dan dengan skema Ewald (c).
Alih-alih sebuah kesimpulan
Perhatikan bahwa struktur yang diperoleh pada gambar tidak sesuai dengan kisi kristal NaCl, melainkan dengan kisi ZnS, tetapi ini sudah merupakan keluhan tentang potensi pasangan. Memperhatikan elektrostatik sangat penting untuk pemodelan dinamika molekul. Diyakini bahwa itu adalah interaksi elektrostatik yang bertanggung jawab untuk pembentukan kisi kristal, karena ia bertindak pada jarak yang jauh. Benar, dari posisi ini sulit dijelaskan bagaimana zat seperti argon mengkristal selama pendinginan.
Selain metode Ewald yang disebutkan, ada juga metode akuntansi elektrostatik lainnya, lihat, misalnya, ulasan ini .