Pembelajaran mesin (ML) sudah mengubah dunia. Google menggunakan IO untuk menawarkan dan menampilkan respons terhadap pencarian pengguna. Netflix menggunakannya untuk merekomendasikan film untuk malam itu. Dan Facebook menggunakannya untuk menyarankan teman-teman baru yang mungkin Anda kenal.
Pembelajaran mesin tidak pernah lebih penting dan, pada saat yang sama, sangat sulit untuk dipelajari. Area ini penuh dengan jargon, dan jumlah algoritma ML yang berbeda bertambah setiap tahun.
Artikel ini akan memperkenalkan Anda pada konsep dasar dalam pembelajaran mesin. Lebih khusus lagi, kita akan membahas konsep dasar dari 9 algoritma ML paling penting saat ini.
Sistem rekomendasi
Untuk membangun sistem rekomendasi yang lengkap dari 0, dibutuhkan pengetahuan mendalam tentang aljabar linier. Karena itu, jika Anda belum pernah mempelajari disiplin ini, mungkin sulit bagi Anda untuk memahami beberapa konsep di bagian ini.
Tapi jangan khawatir - pustaka Python scikit-learn membuatnya cukup mudah untuk membangun CP. Jadi Anda tidak perlu pengetahuan mendalam tentang aljabar linier untuk membangun CP yang berfungsi.
Bagaimana cara kerja CP?
Ada 2 jenis utama sistem rekomendasi:
- Berbasis konten
- Penyaringan kolaboratif
Sistem berbasis konten membuat rekomendasi berdasarkan kesamaan elemen yang sudah Anda gunakan. Sistem ini berperilaku persis seperti yang Anda harapkan dari CP.
Pemfilteran kolaboratif CP memberikan rekomendasi berdasarkan pengetahuan tentang bagaimana pengguna berinteraksi dengan elemen (* catatan: interaksi dengan elemen pengguna lain yang memiliki perilaku yang mirip dengan pengguna diambil sebagai basis). Dengan kata lain, mereka menggunakan "kebijaksanaan kerumunan" (karenanya "kolaboratif" atas nama metode).
Di dunia nyata, penyaringan CP kolaboratif jauh lebih umum daripada sistem berbasis konten. Ini terutama disebabkan oleh fakta bahwa mereka biasanya memberikan hasil yang lebih baik. Beberapa ahli juga menemukan sistem kolaboratif lebih mudah dipahami.
Penyaringan kolaboratif CP juga memiliki fitur unik yang tidak ditemukan dalam sistem berbasis konten. Yaitu, mereka memiliki kemampuan untuk mempelajari fitur sendiri.
Ini berarti bahwa mereka bahkan dapat mulai mendefinisikan kesamaan dalam elemen-elemen berdasarkan pada sifat-sifat atau sifat-sifat yang Anda bahkan tidak sediakan untuk sistem ini bekerja.
Ada 2 subkategori penyaringan kolaboratif:
- Berbasis Model
- Berbasis lingkungan
Berita baiknya adalah Anda tidak perlu tahu perbedaan antara kedua jenis filter CP kolaboratif ini untuk menjadi sukses di ML. Cukup hanya mengetahui bahwa ada beberapa jenis.
Meringkaskan
Berikut rekap singkat dari apa yang telah kami pelajari tentang sistem rekomendasi dalam artikel ini:
- Contoh-contoh sistem rekomendasi dunia nyata
- Berbagai jenis sistem rekomendasi dan mengapa pemfilteran kolaboratif lebih sering digunakan daripada sistem berbasis konten
- Hubungan antara sistem rekomendasi dan aljabar linier
Regresi linier
Regresi linier digunakan untuk memprediksi beberapa nilai y berdasarkan sekumpulan nilai x.
Sejarah regresi linier
Regresi linier (LR) ditemukan pada tahun 1800 oleh Francis Galton. Galton adalah seorang ilmuwan yang mempelajari ikatan antara orang tua dan anak-anak. Lebih khusus lagi, Galton menyelidiki hubungan antara pertumbuhan ayah dan pertumbuhan putra mereka. Penemuan pertama Galton adalah fakta bahwa pertumbuhan anak laki-laki, pada umumnya, hampir sama dengan pertumbuhan ayah mereka. Yang tidak mengejutkan.
Belakangan, Galton menemukan sesuatu yang lebih menarik. Pertumbuhan anak laki-laki, sebagai suatu peraturan, lebih dekat dengan tinggi keseluruhan rata-rata semua orang daripada pertumbuhan ayahnya sendiri.
Galton menyebut fenomena ini regresi . Secara khusus, ia berkata: "Tinggi anak laki-laki cenderung mundur (atau bergeser ke) tinggi rata-rata."
Ini menyebabkan seluruh bidang dalam statistik dan pembelajaran mesin yang disebut regresi.
Matematika Regresi Linier
Dalam proses membuat model regresi, semua yang kami coba lakukan adalah menggambar garis sedekat mungkin dengan setiap titik dalam dataset.
Contoh khas dari pendekatan ini adalah pendekatan regresi linier "kuadrat", yang menghitung kedekatan garis dalam arah naik-turun.
Contoh untuk ilustrasi:
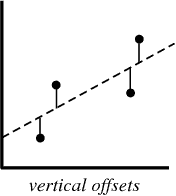
Saat Anda membuat model regresi, produk akhir Anda adalah persamaan yang dapat Anda gunakan untuk memprediksi nilai y untuk nilai x tanpa mengetahui nilai y sebelumnya.
Regresi logistik
Regresi logistik mirip dengan regresi linier, kecuali bahwa alih-alih menghitung nilai y, ia mengevaluasi kategori yang dimiliki oleh titik data tertentu.
Apa itu Regresi Logistik?
Regresi logistik adalah model pembelajaran mesin yang digunakan untuk memecahkan masalah klasifikasi.
Di bawah ini adalah beberapa contoh tugas klasifikasi MO:
- Email spam (spam atau bukan spam?)
- Klaim asuransi mobil (kompensasi atau perbaikan?)
- Diagnosis penyakit
Masing-masing tugas ini jelas memiliki 2 kategori, menjadikannya contoh tugas klasifikasi biner.
Regresi logistik bekerja dengan baik untuk masalah klasifikasi biner - kami hanya menetapkan kategori yang berbeda masing-masing untuk 0 dan 1.
Mengapa Regresi Logistik? Karena Anda tidak dapat menggunakan regresi linier untuk prediksi klasifikasi biner. Ini tidak akan berhasil karena Anda akan mencoba menggambar garis lurus melalui dataset dengan dua nilai yang mungkin.
Gambar ini dapat membantu Anda memahami mengapa regresi linier buruk untuk klasifikasi biner:
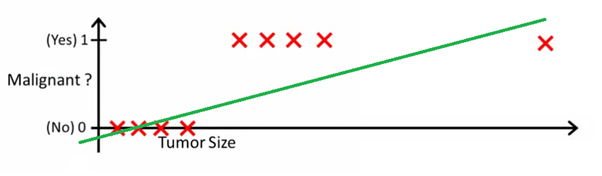
Pada gambar ini, sumbu y mewakili probabilitas bahwa tumor tersebut ganas. Nilai 1-y mewakili probabilitas bahwa tumor tersebut jinak. Seperti yang Anda lihat, model regresi linier berkinerja sangat buruk untuk memprediksi kemungkinan sebagian besar pengamatan dalam dataset.
Inilah mengapa model regresi logistik berguna. Ini memiliki tikungan menuju garis paling pas, yang membuatnya jauh lebih cocok untuk memprediksi data kualitatif (kategorikal).
Berikut adalah contoh yang membandingkan model regresi linier dan logistik pada data yang sama:
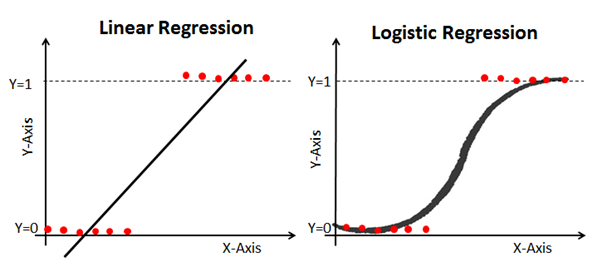
Sigmoid (Fungsi Sigmoid)
Alasan regresi logistik kinked adalah karena tidak menggunakan persamaan linier untuk menghitungnya. Sebaliknya, model regresi logistik dibangun menggunakan sigmoid (juga disebut fungsi logistik karena digunakan dalam regresi logistik).
Anda tidak harus menghafal sigmoid secara menyeluruh untuk berhasil di ML. Meski demikian, akan sangat membantu jika Anda memiliki ide tentang fitur ini.
Sigmoid Formula:
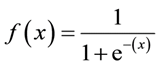
Karakteristik utama sigmoid, yang layak ditangani - tidak peduli berapa pun nilai yang Anda berikan ke fungsi ini, ia akan selalu mengembalikan nilai dalam kisaran 0-1.
Menggunakan model regresi logistik untuk prediksi
Untuk menggunakan regresi logistik untuk prediksi, Anda biasanya perlu menentukan titik cutoff secara akurat. Titik batas ini biasanya 0,5.
Mari kita gunakan contoh diagnosis kanker kami dari grafik sebelumnya untuk melihat prinsip ini dalam praktiknya. Jika model regresi logistik mengembalikan nilai di bawah 0,5, maka titik data tersebut akan dikategorikan sebagai jinak. Demikian pula, jika sigmoid memberi nilai di atas 0,5, maka tumor tersebut tergolong ganas.
Menggunakan matriks kesalahan untuk mengukur efektivitas regresi logistik
Matriks kesalahan dapat digunakan sebagai alat untuk membandingkan skor benar positif, benar negatif, positif salah, dan negatif palsu di MO.
Matriks kesalahan sangat berguna ketika digunakan untuk mengukur kinerja model regresi logistik. Berikut adalah contoh bagaimana kita dapat menggunakan matriks kesalahan:
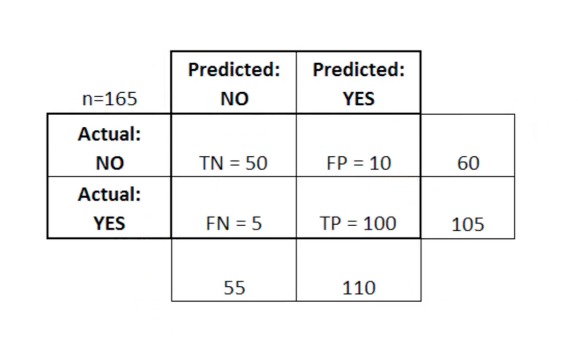
Dalam tabel ini TN berarti benar negatif, FN singkatan negatif palsu, FP singkatan positif palsu, TP singkatan benar positif.
Matriks kesalahan berguna untuk mengevaluasi suatu model jika ada kuadran "lemah" dalam matriks kesalahan. Sebagai contoh, dia mungkin memiliki jumlah positif palsu yang sangat tinggi.
Dalam beberapa kasus, ini juga cukup berguna untuk memastikan bahwa model Anda bekerja dengan benar di area berbahaya dari matriks kesalahan.
Dalam contoh diagnosis kanker ini, misalnya, Anda ingin memastikan bahwa model Anda tidak memiliki terlalu banyak positif palsu karena ini berarti Anda mendiagnosis tumor ganas seseorang sebagai jinak.
Meringkaskan
Di bagian ini, Anda berkenalan pertama dengan model ML - regresi logistik.
Berikut ini ringkasan singkat tentang apa yang telah Anda pelajari tentang regresi logistik:
- Jenis masalah klasifikasi yang cocok untuk diselesaikan dengan regresi logistik
- Fungsi logistik (sigmoid) selalu memberikan nilai antara 0 dan 1
- Cara menggunakan cut-off points untuk memprediksi dengan model regresi logistik
- Mengapa matriks kesalahan bermanfaat untuk mengukur kinerja model regresi logistik
Algoritma Tetangga K-Terdekat
Algoritma k-tetangga terdekat dapat membantu memecahkan masalah klasifikasi dalam kasus ketika ada lebih dari 2 kategori.
Apa algoritma tetangga terdekat k-terdekat?
Ini adalah algoritma klasifikasi berdasarkan prinsip sederhana. Bahkan, prinsipnya sangat sederhana sehingga yang terbaik adalah menunjukkannya dengan sebuah contoh.
Bayangkan Anda memiliki data tinggi dan berat badan untuk pemain bola dan pemain bola basket. Algoritma tetangga k-terdekat dapat digunakan untuk memprediksi apakah pemain baru adalah pemain sepak bola atau pemain bola basket. Untuk melakukan ini, algoritma menentukan titik data K yang paling dekat dengan objek penelitian.
Gambar ini menunjukkan prinsip ini dengan parameter K = 3:
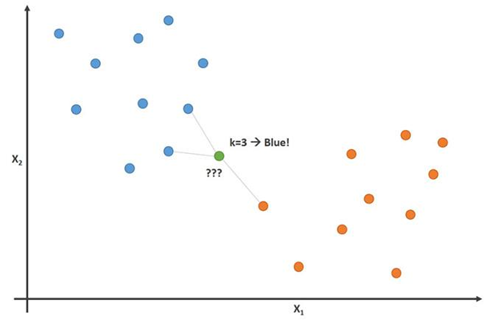
Dalam gambar ini, pemain sepak bola berwarna biru dan pemain bola basket berwarna oranye. Poin yang kami coba klasifikasikan adalah berwarna hijau. Karena sebagian besar (2 dari 3) tanda yang paling dekat dengan titik hijau diwarnai biru (pemain sepak bola), algoritma tetangga terdekat K-memprediksi bahwa pemain baru juga akan menjadi pemain sepak bola.
Cara membangun algoritme tetangga K-terdekat
Langkah-langkah utama untuk membangun algoritma ini:
- Kumpulkan semua data
- Hitung jarak Euclidean dari titik data baru x ke semua titik lain dalam kumpulan data
- Sortir poin dari dataset dengan urutan jarak ke x
- Prediksikan jawaban menggunakan kategori yang sama dengan sebagian besar data K-terdekat ke x
Pentingnya variabel K dalam algoritma tetangga K-terdekat
Meskipun ini mungkin tidak jelas sejak awal, mengubah nilai K dalam algoritme ini akan mengubah kategori yang termasuk dalam titik data baru.
Lebih khusus lagi, terlalu kecil nilai K akan menyebabkan model Anda memprediksi secara akurat pada set data pelatihan, tetapi sangat tidak efektif pada data uji. Juga, memiliki K yang terlalu tinggi akan membuat model menjadi tidak perlu menjadi rumit.
Ilustrasi di bawah ini menunjukkan efek ini dengan sempurna:
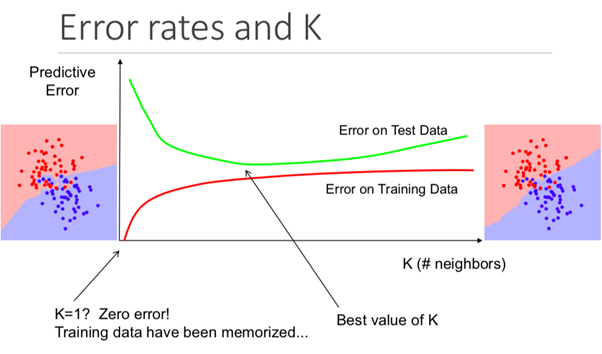
Pro dan kontra dari algoritma tetangga K-terdekat
Untuk meringkas pengantar kami untuk algoritma ini, mari kita bahas secara singkat pro dan kontra dari penggunaannya.
Pro:
- Algoritma ini sederhana dan mudah dimengerti
- Pelatihan model sepele tentang data pelatihan baru
- Bekerja dengan sejumlah kategori dalam tugas klasifikasi
- Mudah menambahkan lebih banyak data ke banyak data
- Model hanya membutuhkan 2 parameter: K dan metrik jarak yang ingin Anda gunakan (biasanya jarak Euclidean)
Minus:
- Biaya komputasi tinggi, karena Anda perlu memproses seluruh jumlah data
- Tidak berfungsi dengan baik dengan parameter kategorikal
Meringkaskan
Ringkasan tentang apa yang baru saja Anda pelajari tentang Algoritma Neighbourhood K-Nearest:
- Contoh masalah klasifikasi (pemain sepak bola atau bola basket) yang dapat dipecahkan algoritma tersebut
- Bagaimana algoritma menggunakan jarak Euclidean ke titik-titik tetangga untuk memprediksi kategori mana yang dimiliki oleh titik data baru
- Mengapa nilai K penting untuk peramalan
- Pro dan kontra menggunakan algoritma tetangga K-terdekat
Pohon Keputusan dan Hutan Acak
Pohon keputusan dan hutan acak adalah 2 contoh metode pohon. Lebih tepatnya, pohon keputusan adalah model ML yang digunakan untuk memprediksi dengan perulangan melalui setiap fungsi dalam dataset satu per satu. Hutan acak adalah ensemble (komite) pohon keputusan yang menggunakan perintah acak objek dalam dataset.
Apa itu metode pohon?
Sebelum kita menyelami dasar-dasar teori metode berbasis pohon di ML, akan sangat membantu untuk memulai dengan sebuah contoh.
Bayangkan Anda bermain basket setiap hari Senin. Selain itu, Anda selalu mengundang teman yang sama untuk datang dan bermain dengan Anda. Terkadang seorang teman datang, terkadang tidak. Keputusan untuk datang atau tidak tergantung pada banyak faktor: seperti apa cuaca, suhu, angin dan kelelahan. Anda mulai memperhatikan fitur-fitur ini dan melacaknya bersama dengan keputusan teman Anda untuk bermain atau tidak.
Anda dapat menggunakan data ini untuk memprediksi apakah teman Anda datang hari ini atau tidak. Salah satu teknik yang dapat Anda gunakan adalah pohon keputusan. Begini tampilannya:
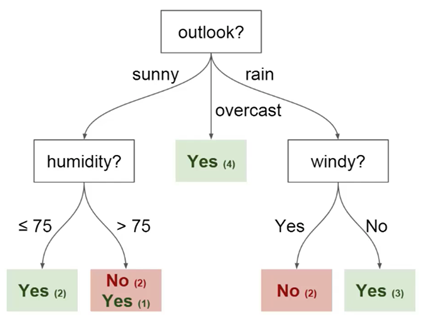
Setiap pohon keputusan memiliki 2 jenis elemen:
- Node: tempat di mana pohon dibagi berdasarkan nilai parameter tertentu
- Tepi: hasil perpecahan mengarah ke simpul berikutnya
Anda dapat melihat bahwa diagram memiliki simpul untuk pandangan, kelembaban dan
berangin. Dan juga aspek untuk setiap nilai potensial dari masing-masing parameter ini.
Berikut adalah beberapa definisi yang harus Anda pahami sebelum kita mulai:
- Root - simpul dari mana pembagian pohon dimulai
- Daun - simpul akhir yang memprediksi hasil akhir
Anda sekarang memiliki pemahaman dasar tentang apa itu pohon keputusan. Kita akan melihat cara membangun pohon seperti itu dari awal di bagian selanjutnya.
Cara membangun pohon keputusan dari awal
Membangun pohon keputusan lebih sulit daripada kedengarannya. Ini karena memutuskan konsekuensi (karakteristik) mana yang akan membagi data Anda (yang merupakan topik dari bidang entropi dan akuisisi data) adalah tugas yang sulit secara matematis.
Untuk mengatasi masalah ini, spesialis ML biasanya menggunakan banyak pohon keputusan, menerapkan serangkaian karakteristik acak yang dipilih untuk membagi pohon ke dalamnya. Dengan kata lain, set karakteristik acak baru dipilih untuk setiap pohon terpisah, di setiap partisi terpisah. Teknik ini disebut hutan acak.
Secara umum, para ahli biasanya memilih ukuran set fitur acak (dilambangkan dengan m) sehingga merupakan akar kuadrat dari total jumlah fitur dalam dataset (dilambangkan dengan p). Singkatnya, m adalah akar kuadrat dari p, dan kemudian karakteristik spesifik dipilih secara acak dari m.
Manfaat menggunakan hutan acak
Bayangkan Anda bekerja dengan banyak data yang memiliki satu karakteristik "kuat". Dengan kata lain, ada karakteristik dalam dataset ini yang jauh lebih dapat diprediksi dalam hal hasil akhir daripada karakteristik lain dari dataset ini.
Jika Anda sedang membangun pohon keputusan dengan tangan, maka masuk akal untuk menggunakan karakteristik ini untuk partisi "atas" di pohon Anda. Ini berarti Anda akan memiliki beberapa pohon yang prediksinya sangat berkorelasi.
Kami ingin menghindari ini karena menggunakan rata-rata variabel yang sangat berkorelasi tidak secara signifikan mengurangi varians. Dengan menggunakan set karakteristik acak untuk setiap pohon di hutan acak, kami menghias pohon dan varians dari model yang dihasilkan berkurang. Hubungan dekorasi ini adalah keuntungan utama dalam menggunakan hutan acak di atas pohon keputusan buatan tangan.
Meringkaskan
Jadi, inilah ringkasan singkat tentang apa yang baru saja Anda pelajari tentang pohon keputusan dan hutan acak:
- Contoh masalah yang solusinya dapat diprediksi menggunakan pohon keputusan
- Elemen pohon keputusan: simpul, wajah, akar, dan daun
- Bagaimana menggunakan seperangkat karakteristik acak memungkinkan kita untuk membangun hutan acak
- Mengapa menggunakan hutan acak untuk dekorelasi variabel dapat berguna dalam mengurangi varians dari model yang dihasilkan
Mendukung Mesin Vektor
Mesin-mesin dukungan vektor adalah suatu algoritma klasifikasi (walaupun, secara teknis, mereka juga dapat digunakan untuk menyelesaikan masalah regresi) yang membagi sekumpulan data ke dalam kategori-kategori dengan "celah" terbesar di antara kategori-kategori. Konsep ini menjadi lebih jelas ketika Anda melihat contoh berikut.
Apa itu mesin vektor dukungan?
Support vector machine (SVM) adalah model ML yang diawasi dengan algoritma pembelajaran yang sesuai yang menganalisis data dan mengenali pola. SVM dapat digunakan untuk tugas klasifikasi dan analisis regresi. Pada artikel ini, kita akan melihat secara khusus menggunakan mesin vektor dukungan untuk menyelesaikan masalah klasifikasi.
Bagaimana cara kerja MOU?
Mari selami bagaimana MOU ini bekerja.
Kami diberi satu set contoh pelatihan, yang masing-masing ditandai sebagai milik salah satu dari 2 kategori, dan menggunakan set SVM ini kami membuat model. Model ini mengkategorikan contoh baru menjadi satu dari dua kategori. Hal ini membuat SVM menjadi classifier linear biner yang tidak mungkin.
MOU menggunakan geometri untuk membuat prediksi berdasarkan kategori. Lebih khusus lagi, mesin vektor dukungan memetakan titik data sebagai titik di ruang dan mengkategorikan mereka sehingga mereka dipisahkan oleh celah selebar mungkin. Prediksi bahwa titik data baru akan menjadi milik kategori tertentu didasarkan pada sisi break point mana.
Berikut adalah contoh visualisasi untuk membantu Anda memahami intuisi MOU:
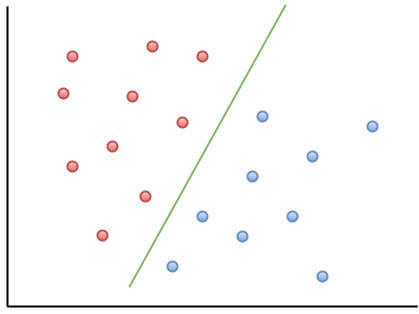
Seperti yang dapat Anda amati, jika titik data baru jatuh di sebelah kiri garis hijau, itu akan disebut sebagai "merah", dan jika ke kanan, itu akan disebut sebagai "biru". Garis hijau ini disebut hyperplane dan merupakan istilah penting untuk bekerja dengan MOU.
Mari kita lihat representasi visual SVM berikut ini:
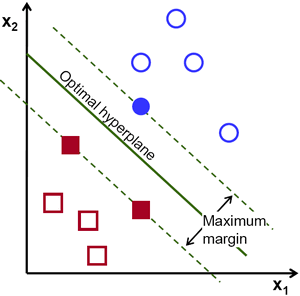
Dalam diagram ini, hyperplane diberi label sebagai "hyperplane optimal". Teori Support Vector Machine mendefinisikan hyperplane optimal sebagai hyperplane yang memaksimalkan bidang antara dua titik data terdekat dari berbagai kategori.
Seperti yang Anda lihat, batas bidang memang mempengaruhi 3 titik data - 2 dari kategori merah dan 1 dari biru. Titik-titik ini, yang bersentuhan dengan batas lapangan, disebut vektor dukungan - karena itulah namanya.
Meringkaskan
Berikut adalah snapshot cepat dari apa yang baru Anda pelajari tentang mesin vektor dukungan:
- MOU adalah contoh dari algoritma ML yang diawasi
- Vektor pendukung dapat digunakan untuk menyelesaikan masalah klasifikasi dan analisis regresi.
- Bagaimana MOU mengkategorikan data menggunakan hyperplane yang memaksimalkan margin antara kategori dalam dataset
- Poin data yang menyentuh batas bidang pemisah disebut vektor dukungan. Di sinilah nama metode berasal.
K-Means Clustering
Metode K-Means adalah algoritma pembelajaran mesin tanpa pengawasan. Ini berarti bahwa ia menerima data yang tidak ditandai dan mencoba untuk mengelompokkan kelompok-kelompok pengamatan serupa dalam data Anda. Metode K-Means sangat berguna untuk menyelesaikan aplikasi dunia nyata. Berikut adalah beberapa contoh tugas yang sesuai dengan model ini:
- Segmentasi pelanggan untuk tim pemasaran
- Klasifikasi dokumen
- Mengoptimalkan rute pengiriman untuk perusahaan seperti Amazon, UPS atau FedEx
- Mengidentifikasi dan merespons lokasi kriminal di kota
- Analisis olahraga profesional
- Memprediksi dan mencegah kejahatan dunia maya
Tujuan utama dari metode K-Means adalah untuk membagi kumpulan data menjadi kelompok-kelompok yang dapat dibedakan sehingga unsur-unsur dalam setiap kelompok serupa satu sama lain.
Berikut ini adalah representasi visual dari apa yang tampak dalam praktiknya:
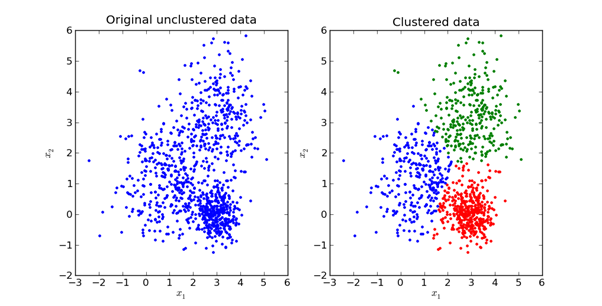
Kami akan mengeksplorasi matematika di balik metode K-Means di bagian selanjutnya dari artikel ini.
Bagaimana cara kerja metode K-Means?
Langkah pertama dalam menggunakan metode K-Means adalah memilih jumlah grup yang ingin Anda bagi data Anda. Kuantitas ini adalah nilai K, tercermin dalam nama algoritma. Pilihan nilai K dalam metode K-Means sangat penting. Kami akan membahas cara memilih nilai K yang benar sedikit kemudian.
Selanjutnya, Anda harus secara acak memilih titik dalam dataset dan menetapkannya ke cluster acak. Ini akan memberi Anda posisi data awal di mana Anda menjalankan iterasi berikutnya sampai cluster berhenti berubah:
- Menghitung centroid (pusat gravitasi) dari setiap kluster dengan mengambil vektor rata-rata titik dalam kluster tersebut
- Tetapkan kembali setiap titik data ke cluster yang centroidnya paling dekat dengan titik tersebut
Memilih Nilai K yang Tepat dalam Metode K-Means
Sebenarnya, memilih nilai K yang cocok cukup sulit. Tidak ada jawaban "benar" dalam memilih nilai K. "terbaik." Salah satu metode yang sering digunakan para profesional ML disebut "metode siku".
Untuk menggunakan metode ini, hal pertama yang perlu Anda lakukan adalah menghitung jumlah kesalahan kuadrat - standar deviasi untuk algoritma Anda untuk sekelompok nilai K. Standar deviasi dalam metode K-means didefinisikan sebagai jumlah kuadrat dari jarak antara setiap titik data dalam cluster. dan pusat gravitasi dari kluster ini.
Sebagai contoh dari langkah ini, Anda dapat menghitung deviasi standar untuk nilai K dari 2, 4, 6, 8, dan 10. Selanjutnya, Anda akan ingin menghasilkan grafik deviasi standar dan nilai-nilai K. Anda akan melihat bahwa deviasi berkurang dengan meningkatnya nilai K.
Dan masuk akal: semakin banyak kategori yang Anda buat dari satu set data, semakin besar kemungkinan setiap titik data akan dekat dengan pusat dari cluster titik itu.
Dengan mengatakan itu, ide utama di balik metode siku adalah untuk memilih nilai K di mana RMS akan secara dramatis memperlambat laju penurunan. Penurunan tajam ini membentuk "siku" pada grafik.
Sebagai contoh, berikut adalah plot RMS versus K. Dalam hal ini, metode siku akan menyarankan menggunakan nilai K sekitar 6.
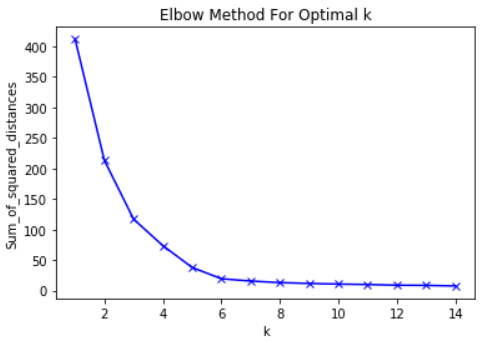
Penting bahwa K = 6 hanyalah perkiraan nilai K yang dapat diterima. Tidak ada nilai K "terbaik" dalam metode K-Means. Seperti banyak hal dalam ML, ini adalah keputusan yang sangat situasional.
Meringkaskan
Berikut ini sketsa singkat dari apa yang baru saja Anda pelajari di bagian ini:
- Contoh tugas ML tanpa guru yang dapat diselesaikan dengan metode K-means
- Prinsip dasar metode K-means
- Cara Kerja K-Means
- Cara menggunakan metode siku untuk memilih nilai yang sesuai untuk parameter K dalam algoritma ini
Analisis Komponen Utama
Analisis komponen utama digunakan untuk mengubah dataset dengan banyak parameter menjadi dataset baru dengan parameter lebih sedikit, dan setiap parameter baru dalam dataset ini adalah kombinasi linear dari parameter yang sudah ada sebelumnya. Data yang diubah ini cenderung membenarkan banyak varian dari dataset asli dengan jauh lebih sederhana.
Apa itu Metode Komponen Utama?
Principal component analysis (PCA) adalah teknik ML yang digunakan untuk mempelajari hubungan antara set variabel. Dengan kata lain, PCA memeriksa set variabel untuk menentukan struktur dasar dari variabel-variabel ini. PCA juga kadang-kadang disebut analisis faktor.
Berdasarkan uraian ini, Anda mungkin berpikir bahwa PCA sangat mirip dengan regresi linier. Tapi ini bukan masalahnya. Padahal, 2 teknik ini memiliki beberapa perbedaan penting.
Perbedaan antara regresi linier dan PCA
Regresi linier menentukan garis paling cocok di seluruh dataset. Analisis komponen utama mengidentifikasi beberapa garis paling cocok orthogonal untuk dataset.
Jika Anda tidak terbiasa dengan istilah orthogonal, maka itu berarti bahwa garis-garis tersebut saling bersinggungan satu sama lain, seperti utara, timur, selatan dan barat pada peta.
Mari kita lihat contoh untuk membantu Anda memahami ini dengan lebih baik.

Lihatlah label sumbu pada gambar ini. Komponen utama dari sumbu x menjelaskan 73% dari varians dalam dataset ini. Komponen utama dari sumbu y menjelaskan sekitar 23% dari varians dalam dataset.
Ini berarti bahwa 4% dari varians tetap tidak dapat dijelaskan. Anda dapat mengurangi angka ini dengan menambahkan lebih banyak komponen utama ke analisis Anda.
Meringkaskan
Ringkasan tentang apa yang baru Anda pelajari tentang analisis komponen utama:
- PCA mencoba menemukan faktor ortogonal yang menentukan variabilitas dalam dataset
- Perbedaan antara regresi linier dan PCA
- Seperti apa komponen utama ortogonal ketika dirender dalam dataset
- Itu menambahkan komponen utama tambahan dapat membantu menjelaskan varians lebih akurat dalam dataset