Ingat algoritma Dijkstra
Algoritma Dijkstra adalah salah satu algoritma teori grafik paling populer. Ini digunakan untuk menemukan jalur terpendek antara node pada grafik yang diarahkan. Kita mulai dengan node sumber dan panjang tepi yang diketahui antara node.
Pertama, kami menetapkan jarak dari sumber ke semua node. Node s mendapatkan nilai 0 karena merupakan sumber; sisanya mendapatkan nilai ∞ untuk memulai.
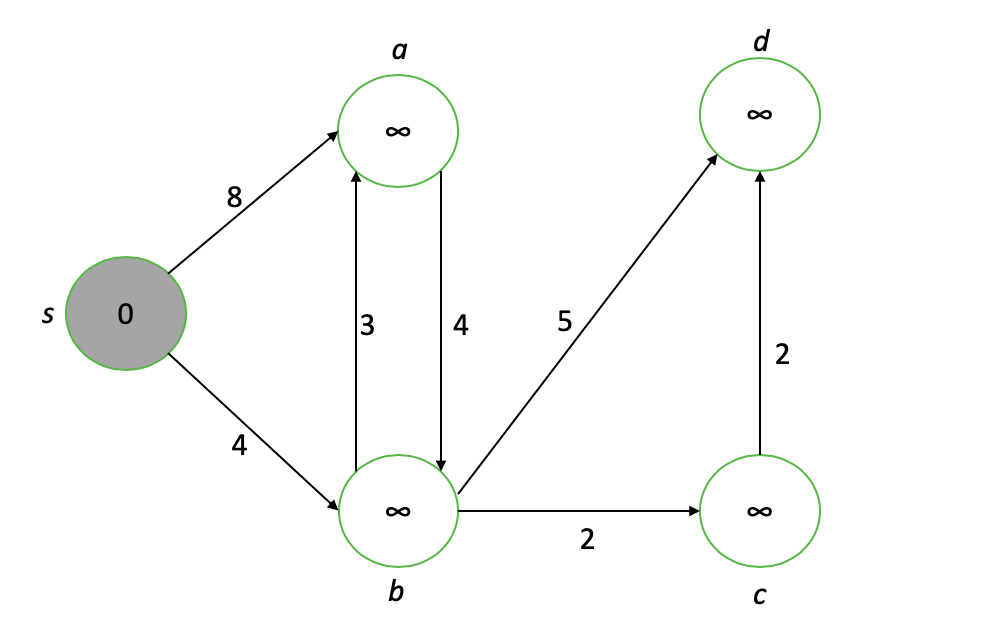
Node kepentingan kami adalah simpul mentah dengan nilai terendah (ditunjukkan dalam warna abu-abu), mis. S. Pertama, kami "melemahkan" setiap simpul yang berdekatan dengan simpul kepentingan kami, memperbarui nilainya ke nilai minimum saat ini atau nilai simpul kepentingan ditambah panjang tepi penghubung ...
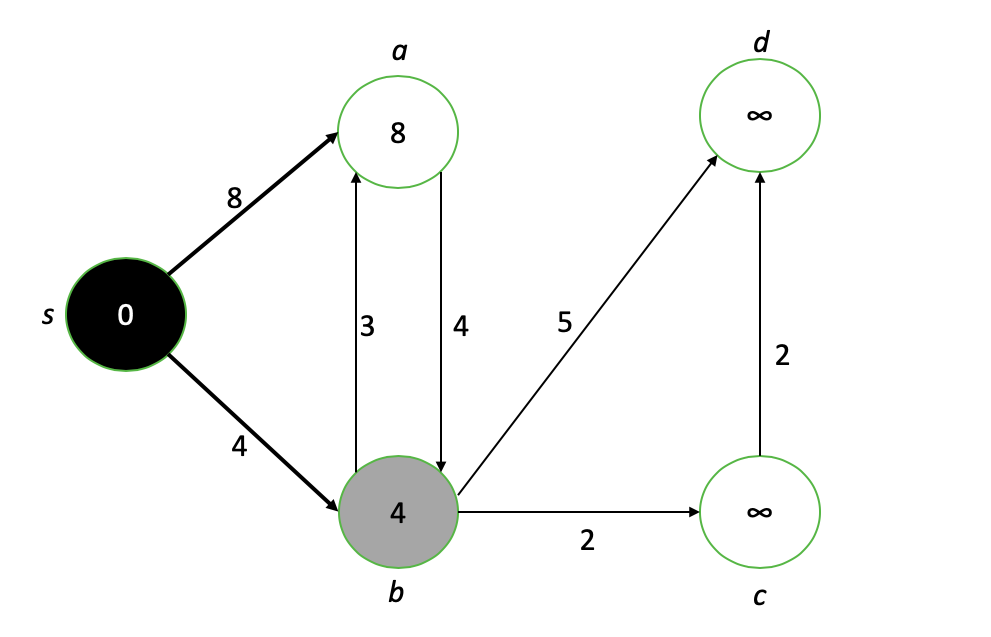
Node s sekarang lengkap (hitam), dan tetangganya a dan b telah mengambil nilai baru. Simpul baru yang menarik adalah b, jadi kami ulangi proses "melemahkan" tetangga b dan menyelesaikan nilai jalur terpendek untuk b.

Setelah melewati setiap node, kita berakhir dengan grafik yang menunjukkan panjang jalur terpendek dari sumber ke setiap node.
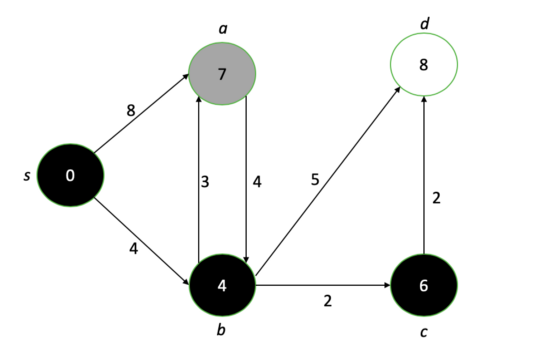


Diagram terakhir kami setelah menjalankan algoritma Dijkstra. Angka-angka pada setiap node mewakili jarak terpendek yang mungkin dari node asli.
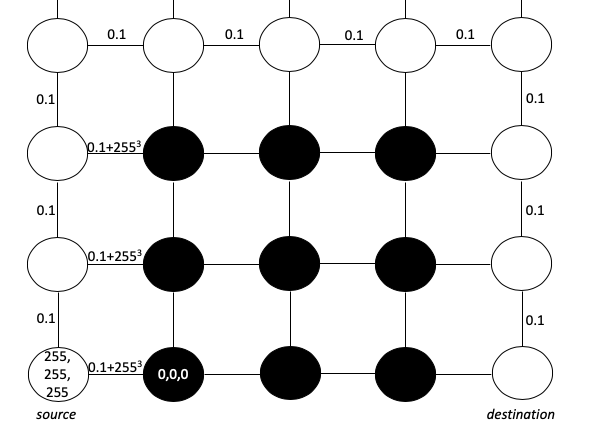
Konseptualisasi gambar labirin.

Kita dapat menganggap gambar sebagai matriks piksel. Setiap piksel (untuk kesederhanaan) memiliki nilai RGB 0,0,0 (hitam) atau 255.255.255 (putih). Tujuan kami adalah membuat jalur terpendek yang dimulai dari warna putih dan tidak menyeberang ke batas hitam. Untuk mewakili tujuan ini, kita dapat mempertimbangkan setiap piksel sebagai simpul dan menggambar tepi antara piksel yang berdekatan dengan panjang tepi berdasarkan perbedaan dalam nilai RGB. Kami akan menggunakan rumus jarak Euclidean persegi dan menambahkan 0,1 untuk memastikan tidak ada panjang jalur 0 - (persyaratan untuk algoritma Dijkstra):
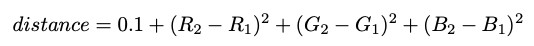
Rumus ini membuat jarak persimpangan melintasi batas labirin terlalu besar. Seperti yang bisa kita lihat, jalur terpendek dari sumber ke tujuan jelas akan melewati penghalang dan tidak melewatinya.
Penerapan
Kita dapat menggunakan OpenCV, pustaka visi Python populer untuk Python, untuk mengekstraksi nilai piksel dan menampilkan gambar labirin kami. Mari kita juga menentukan koordinat lokasi awal dan akhir kami dengan menambahkan poin ke labirin kami.
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()
Kami membuat kelas Vertex untuk membantu kami melacak koordinat. Kami juga ingin melacak simpul induk sehingga kami dapat memulihkan seluruh jalur segera setelah kami menemukan nilai jarak.
class Vertex:
def __init__(self,x_coord,y_coord):
self.x=x_coord
self.y=y_coord
self.d=float('inf') #current distance from source node
self.parent_x=None
self.parent_y=None
self.processed=False
self.index_in_queue=NoneKita perlu membuat matriks vertex yang mewakili susunan piksel dua dimensi dalam gambar. Ini akan menjadi dasar untuk algoritma Dijkstra. Kami juga menjaga antrian dengan tumpukan prioritas minimum untuk melacak node mentah.
def find_shortest_path(img,src,dst):
pq=[] #min-heap priority queue
imagerows,imagecols=img.shape[0],img.shape[1]
matrix = np.full((imagerows, imagecols), None)
#access matrix elements by matrix[row][col]
#fill matrix with vertices
for r in range(imagerows):
for c in range(imagecols):
matrix[r][c]=Vertex(c,r)
matrix[r][c].index_in_queue=len(pq)
pq.append(matrix[r][c])
#set source distance value to 0
matrix[source_y][source_x].d=0
#maintain min-heap invariant (minimum d Vertex at list index 0)
pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)Kami membutuhkan beberapa fungsi pembantu untuk membantu kami menemukan tepi dan panjang tepi antara simpul:
#Implement euclidean squared distance formula
def get_distance(img,u,v):
return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
shape=mat.shape
neighbors=[]
#ensure neighbors are within image boundaries
if r > 0 and not mat[r-1][c].processed:
neighbors.append(mat[r-1][c])
if r < shape[0] - 1 and not mat[r+1][c].processed:
neighbors.append(mat[r+1][c])
if c > 0 and not mat[r][c-1].processed:
neighbors.append(mat[r][c-1])
if c < shape[1] - 1 and not mat[r][c+1].processed:
neighbors.append(mat[r][c+1])
return neighborsSekarang kita dapat mengimplementasikan algoritma Dijkstra dan menetapkan nilai jarak (d) ke semua simpul piksel dalam gambar labirin:
while len(pq) > 0:
u=pq[0] #smallest-value unprocessed node
#remove node of interest from the queue
pq[0]=pq[-1]
pq[0].index_in_queue=0
pq.pop()
pq=bubble_down(pq,0) #min-heap function, see source code
u.processed=True
neighbors = get_neighbors(matrix,u.y,u.x)
for v in neighbors:
dist=get_distance(img,(u.y,u.x),(v.y,v.x))
if u.d + dist < v.d:
v.d = u.d+dist
v.parent_x=u.x #keep track of the shortest path
v.parent_y=u.y
idx=v.index_in_queue
pq=bubble_down(pq,idx)
pq=bubble_up(pq,idx)Sekarang kita dapat memanggil fungsi jalur terpendek dan menggambar solusi di labirin kami:
img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen
plt.show()

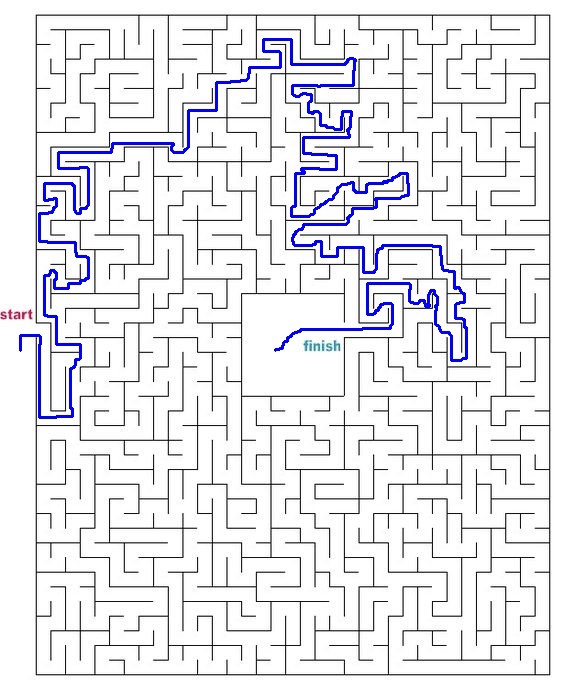
Mari kita coba labirin lain dari seluruh internet.



Kode sumber lengkap tersedia di GitHub di sini .
Lanjutan: Proyek pelatihan Python: antarmuka dengan 40 baris kode (bagian 2)

Pelajari lebih lanjut tentang cara mendapatkan profesi yang dicari dari awal atau Tingkatkan keterampilan dan gaji dengan mengambil kursus online berbayar SkillFactory:
- Kursus Pembelajaran Mesin (12 minggu)
- Belajar Ilmu Data dari awal (12 bulan)
- Profesi analis dengan level awal apa pun (9 bulan)
- «Python -» (9 )