Matematika jarak sosial adalah pelajaran geometri

Tantangan tentang bagaimana membuka kembali kantor, sekolah, dan ruang publik lainnya dengan aman sembari menjaga jarak satu setengah meter adalah pertanyaan yang telah dipelajari oleh para ahli matematika selama berabad-abad.

Tampaknya topik seperti pengemasan bola hanya akan menarik bagi ahli matematika. Siapa lagi yang tertarik mencari cara paling efektif untuk menempatkan lingkaran pada bidang atau bidang di luar angkasa?



Namun, saat ini jutaan orang di seluruh dunia sedang merenungkan tugas ini dengan tepat.



Menentukan cara membuka gedung dan ruang publik dengan aman sambil menjaga jarak sosial, khususnya, merupakan latihan geometri. Jika setiap orang harus berada setidaknya satu setengah meter dari orang lain, lalu untuk menghitung berapa banyak orang yang dapat duduk di kelas atau ruang makan, Anda perlu mengemas lingkaran yang tidak tumpang tindih di denah lantai.







Secara alami, untuk memerangi virus korona, lebih banyak masalah yang perlu diselesaikan daripada masalah geometris ini. Namun, pengemasan lingkaran dan bola berperan dalam hal ini - seperti pemodelan struktur kristal dalam kimia dan ruang pesan abstrak dalam teori informasi. Tugas ini, yang tampaknya sederhana dalam deskripsi, memenuhi pikiran ahli matematika terbesar dalam sejarah, dan penelitian paling menarik di bidang ini dilakukan hari ini, khususnya, dalam dimensi yang lebih tinggi. Misalnya, ahli matematika baru-baru ini menemukan cara terbaik untuk mengemas dalam ruang 8 dan 24 dimensi - teknik yang diperlukan untuk mengoptimalkan kode koreksi kesalahan yang digunakan baik di ponsel maupun dalam komunikasi dengan probe ruang angkasa. Jadi mari kita lihat beberapa komplikasi tak terduga yang muncul saat kita mencoba mengisi ruang dengan formulir paling sederhana.



Baik Anda mengemas jeruk ke dalam kotak di tempat kerja atau menempatkan siswa dengan jarak sosial yang aman, ukuran dan bentuk wadah Anda sangat penting untuk tugas Anda. Namun, bagi kebanyakan matematikawan, teori pengepakan bola adalah tentang mengisi seluruh ruang. Dalam dua dimensi, ini berarti menutupi bidang dengan lingkaran terputus-putus berukuran sama.



Berikut adalah salah satu contoh pengepakan lingkaran di pesawat. Ini terlihat seperti tampilan atas dari kemasan soda:







Bisa dibayangkan bagaimana pola ini berulang ke segala arah, seperti ubin yang telah diaspal dengan bidang datar. Kesenjangan kecil di antara lingkaran menunjukkan bahwa bidang tidak terisi penuh, tetapi dalam kasus lingkaran pengepakan hal ini diharapkan terjadi. Kami tertarik pada persentase cakupan pesawat. Ini akan menjadi "kepadatan pengepakan" dari metode tertentu.



Metode di atas disebut pengepakan persegi, dan untuk alasan yang bagus - pusat lingkaran dapat direpresentasikan sebagai simpul persegi.







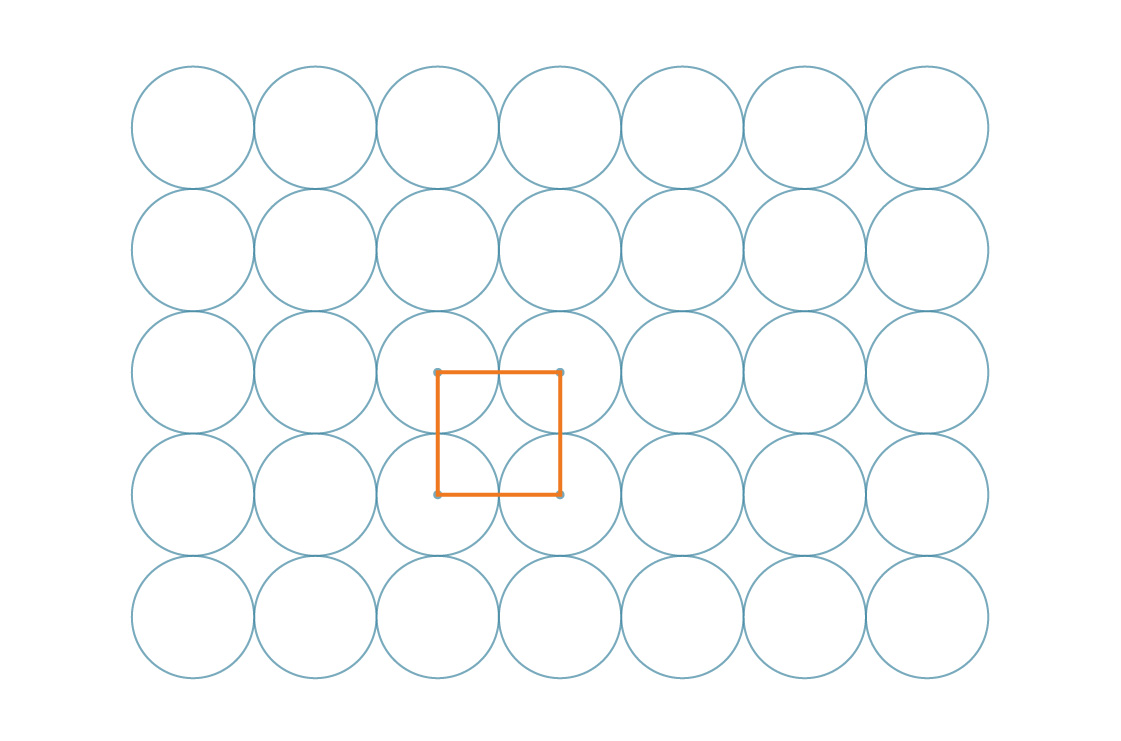
Dan faktanya, bujur sangkar itu sendiri menyusun bidang:







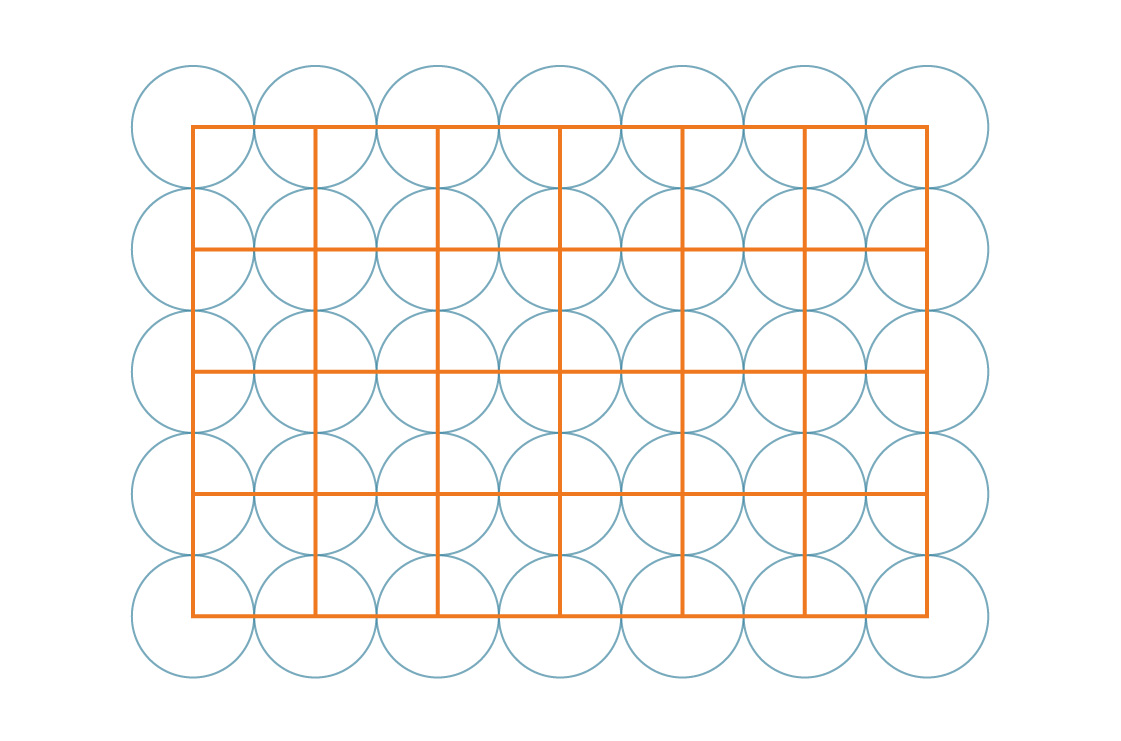
Tugas kita difasilitasi oleh kesimetrisan polanya. Karena bujur sangkar ini menutupi seluruh bidang secara periodik, persentase bidang yang dilingkupi oleh lingkaran sama dengan persentase bujur sangkar yang ditutupi oleh lingkaran. Mari kita lihat salah satu kotak ini.







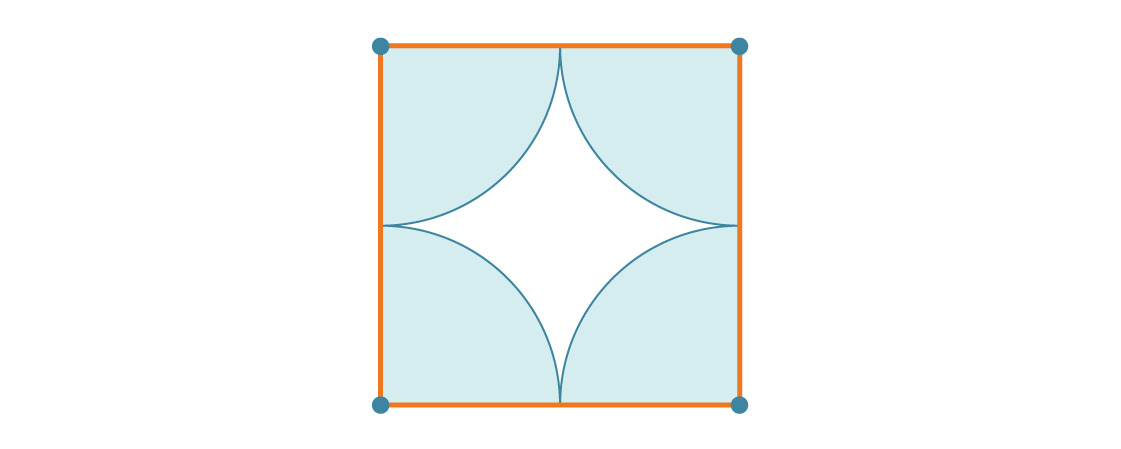
Misalkan jari-jari lingkaran adalah r. Artinya panjang sisi bujur sangkar adalah 2r. Pada setiap simpul persegi ada seperempat lingkaran, sehingga persentase cakupan setiap persegi sama dengan rasio luas satu lingkaran penuh dengan luas satu persegi penuh:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

Setiap bujur sangkar sekitar 78,54% ditutupi dengan lingkaran, jadi dengan mempertimbangkan ubin bidangnya, 78,54% itu ditutupi dengan lingkaran. Ini adalah kerapatan kemasan persegi. Perhatikan bahwa jari-jari r menghilang dari jawaban. Dan ini masuk akal: berapa pun ukuran lingkarannya, masih akan ada empat perempat lingkaran dalam sebuah persegi.



Jika Anda mencoba melipat kaleng soda di sisinya seperti ini, dan kaleng tersebut bergeser dan mengisi celah, Anda tahu bahwa ada cara lain untuk mengemas lingkaran pada bidang:







Mari gunakan pendekatan yang mirip dengan yang sebelumnya, dan bayangkan bahwa pusat lingkaran dalam hal ini membentuk segi enam biasa ...







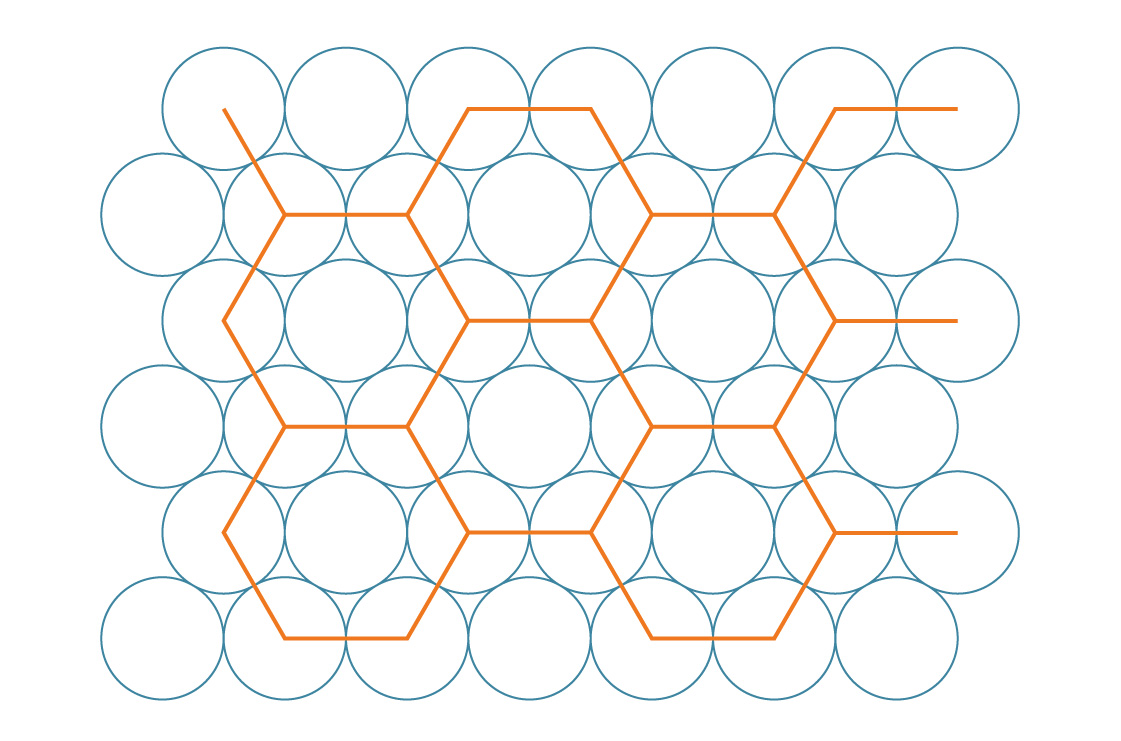
Kami menyebutnya pengepakan heksagonal. Tampaknya metode ini mengisi celah lebih efisien daripada persegi. Untuk memeriksanya, mari bandingkan kepadatan pengemasannya. Segi enam, seperti bujur sangkar, menyusun bidang seluruhnya, sehingga kita dapat menentukan kerapatan metode ini dengan menganalisis satu segi enam.







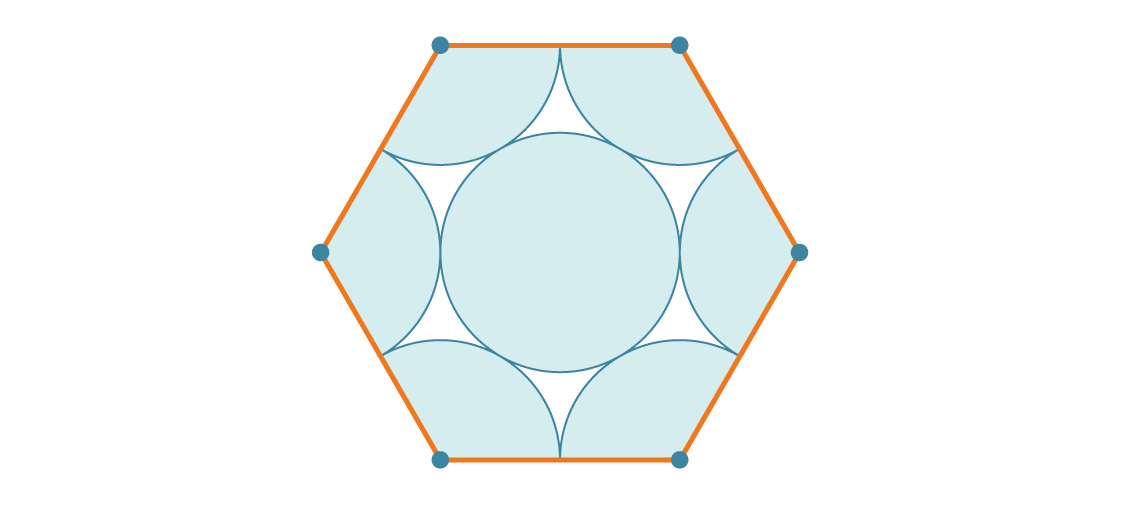
Bagian segi enam mana yang tertutup lingkaran? Karena segi enam biasa memiliki sudut internal 120 °, ada sepertiga lingkaran di masing-masing sudutnya. Ternyata dua lingkaran penuh, dan lingkaran tengah menjadi yang ketiga. Oleh karena itu, setiap segi enam ditutupi oleh tiga lingkaran. Jika jari-jari setiap lingkaran adalah r, maka luasnya adalah 3πr².







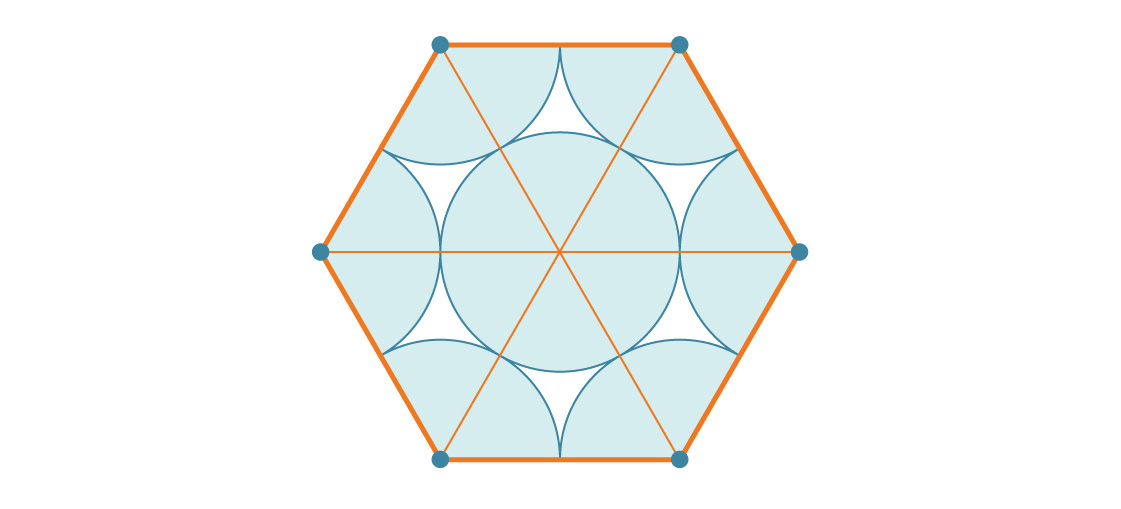
Bagaimana hal ini dibandingkan dengan luas segi enam? Segi enam dengan panjang sisi s adalah enam buah segitiga sama sisi dengan panjang sisinya s, masing-masing adalah s ² √3 / 4. Oleh karena itu, luas segi enam adalah 6 * s ² √3 / 4 = 6 s ² √3 / 4. Karena panjang sisi segi enam kita adalah 2r, luasnya adalah:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

Sekarang Anda bisa menghitung persentase segi enam yang ditutupi oleh lingkaran (dengan membagi luas enam lingkaran dengan luas segi enam):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

Setiap segi enam sekitar 90,69% tertutup lingkaran, jadi kemasan ini akan jauh lebih efisien daripada kemasan persegi. Perhatikan bagaimana jari-jari lingkaran menghilang lagi seperti yang diharapkan. Nyatanya, tidak ada pengemasan yang lebih efisien.



Namun tidak mudah untuk membuktikannya. Matematikawan terkenal seperti Joseph Louis Lagrange dan Karl Friedrich Gauss mulai mengerjakan ini pada akhir abad ke-18 dan awal abad ke-19, tetapi masalah tersebut baru terpecahkan sepenuhnya pada tahun 1940-an, dengan memproses semua pengaturan yang mungkin - periodik dan non-periodik. Fakta bahwa butuh begitu banyak waktu untuk menyelesaikan masalah dalam dua dimensi, di mana segala sesuatu cukup mudah dibayangkan, dapat menjadi peringatan atas apa yang menanti kita di dimensi yang lebih tinggi.



Bola pengemasan dalam tiga dimensi adalah tugas yang jauh lebih sulit, meskipun memiliki beberapa kesamaan dengan sepupu dua dimensinya. Misalnya, paket dua dimensi yang telah kami pertimbangkan terdiri dari satu lapisan.







Untuk paket persegi, kami meletakkan setiap lapisan di atas yang sebelumnya.







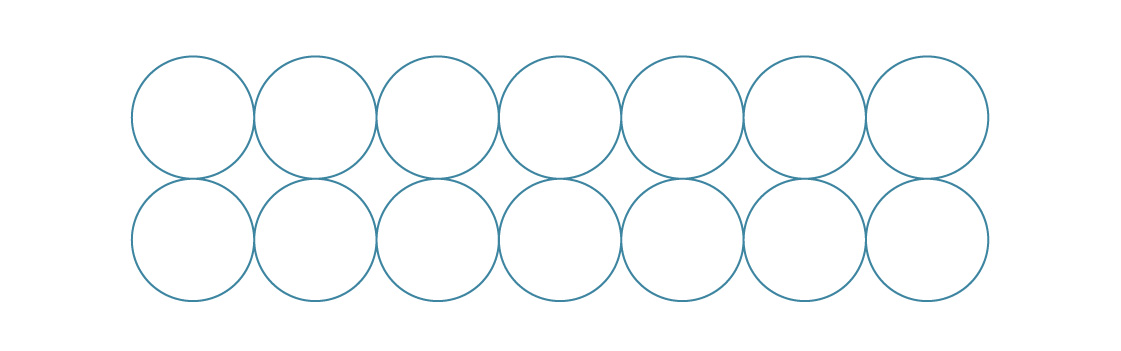
Untuk pengepakan heksagonal, kami menempatkan lapisan baru di antara yang sebelumnya.







Pengemasan yang berbeda diperoleh tergantung pada bagaimana kita menggabungkan salinan dari berbagai lapisan.



Dalam tiga dimensi, susunan lapisan di atas satu sama lain ini menciptakan pengemasan yang berbeda secara fundamental.







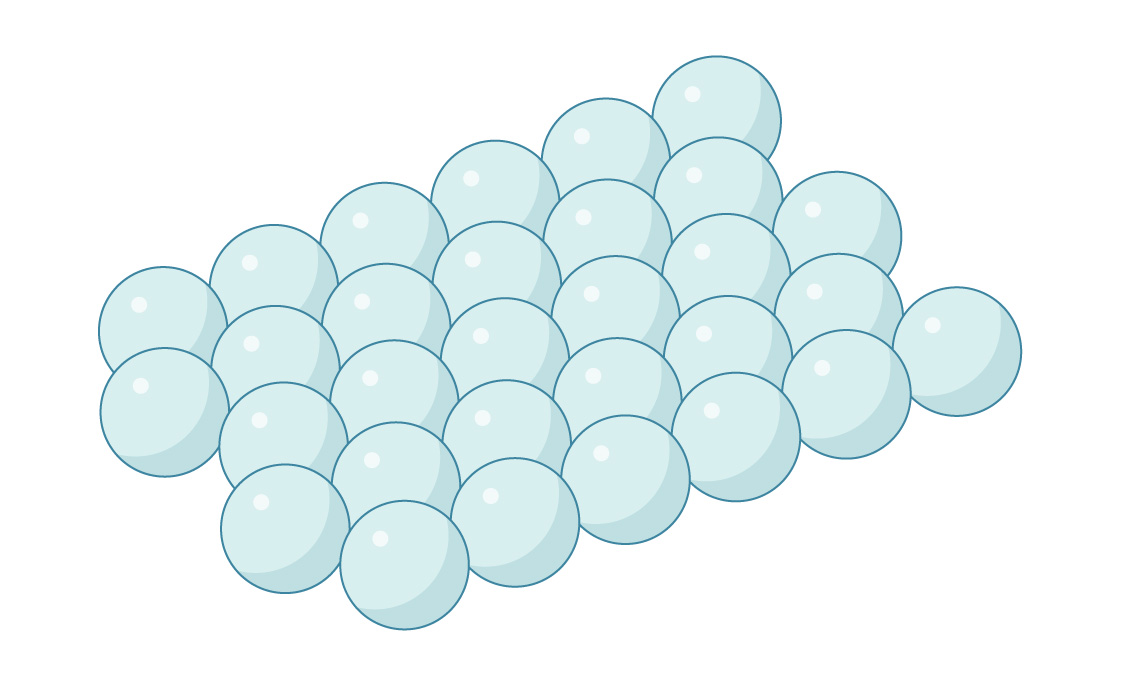
Ini adalah lapisan bola yang dikemas secara heksagonal, seperti yang disarankan oleh pengemasan lingkaran optimal pada bidang. Demikian juga, Anda bisa meletakkan lapisan kedua di atas lapisan pertama dengan menempatkan bola di ruang antara bola bawah.







Namun dalam tiga dimensi, geometri menjadi sedikit lebih rumit. Di setiap lapisan bola, jarak antara celah yang berdekatan ternyata kurang dari jarak antara pusat bola. Oleh karena itu, Anda tidak dapat menempelkan bola ke setiap celah - mereka akan berpotongan. Oleh karena itu, celah di dua lapisan berbaris untuk membuat saluran yang dijalankan melalui paket.







Ada dua cara untuk menempatkan lapisan ketiga. Anda dapat menyelaraskan celah dengan yang paling bawah, dan membiarkan saluran terbuka. Berikut adalah tampilan samping dari pengaturan ini:







Untuk menjaga saluran tetap terbuka, Anda perlu menempatkan bola di lapisan ketiga tepat di atas bola dari lapisan pertama. Susunan bola ini disebut "kemasan padat heksagonal" (silo), dan jika Anda melihatnya dari atas, Anda dapat melihat celah terbuka menembus.







Pilihan lain untuk menempatkan lapisan ketiga adalah menutup saluran. Bola di lapisan ketiga ditempatkan tepat di atas celah lapisan pertama:







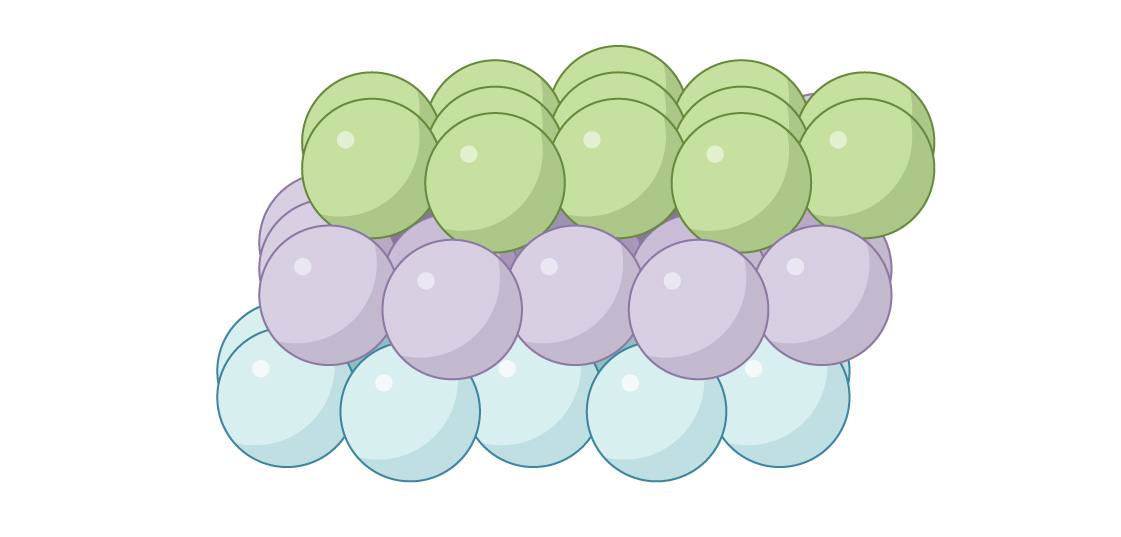
Ini disebut "kubik berpusat muka" (FCC) atau "pengepakan dekat kubik". Jika dilihat dari atas, tidak akan ada celah.







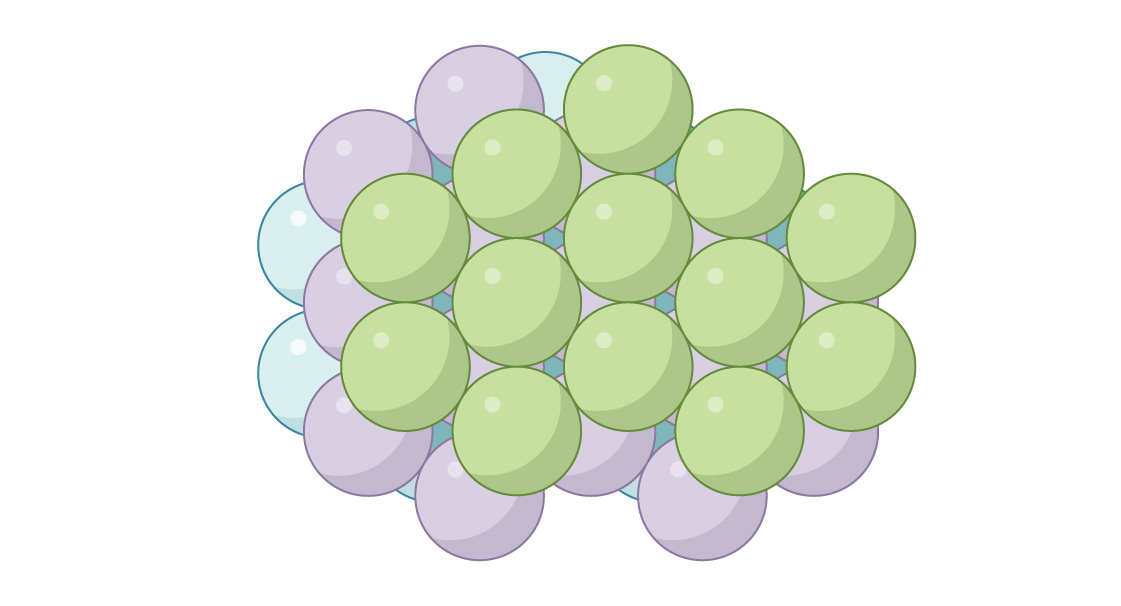
Dua pengaturan yang serupa tetapi berbeda secara fundamental ini muncul dalam kimia, menggambarkan pengaturan atom dalam bahan yang berbeda. Misalnya, pada logam seperti perak dan emas, strukturnya berbentuk HA, dan pada logam seperti seng dan titanium - silo. Setiap metode memungkinkan Anda mengisi ruang dengan bola. Dalam metode silo, di setiap lapisan kedua, bola terletak persis sama, dan di GK - di setiap sepertiga. Anda dapat membuat paket berbeda dalam jumlah tak terbatas dengan menggabungkan kedua metode ini, tetapi yang menarik adalah silo dan GK memberikan paket yang optimal! Kepadatan pengepakannya tidak hanya sama, π 3√2 ≈ 0.7405 adalah pengemasan terpadat yang mungkin ada dalam ruang tiga dimensi. Ahli matematika dan astronom terkenal Johannes Kepler mengemukakan hal ini pada tahun 1611, tetapi merupakan bukti lengkaphanya ahli matematika Thomas Hales yang dapat menyimpulkan pada tahun 1998.







Ada lebih banyak ruang dalam ruang 3D, dan kami memiliki lebih banyak cara untuk mengemas bola secara efektif. Saat Anda menambahkan dimensi, kerumitan pengemasan hanya bertambah - ada lebih banyak ruang, lebih banyak pilihan, dan lebih sulit untuk dibayangkan. Selain itu, bola menjadi lebih kecil dalam dimensi yang lebih tinggi!







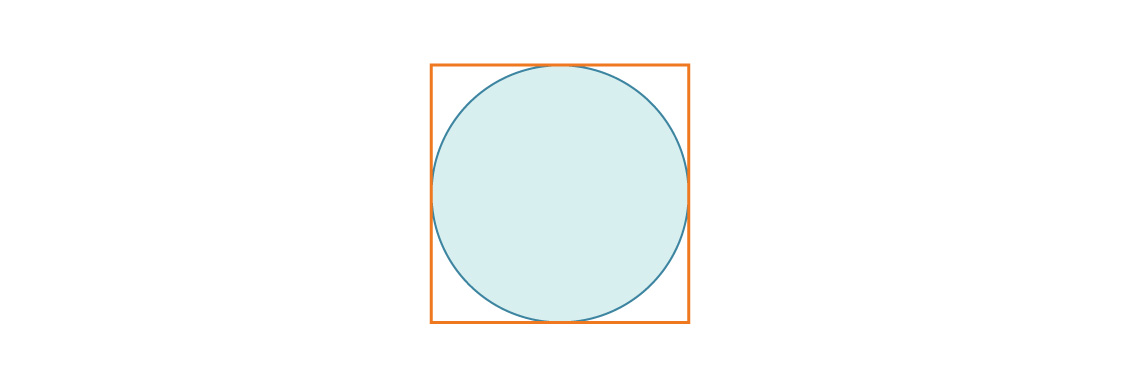
Misalkan sebuah lingkaran bertuliskan bujur sangkar dengan panjang sisi 1.



Jari-jari lingkaran tersebut adalah r = 1/2, sehingga perbandingan luas lingkaran dengan luas persegi adalah:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

Yang juga sama dengan kepadatan pengemasan persegi dalam dua dimensi.



Sekarang mari kita pertimbangkan volume bola yang tertulis dalam kubus satuan.







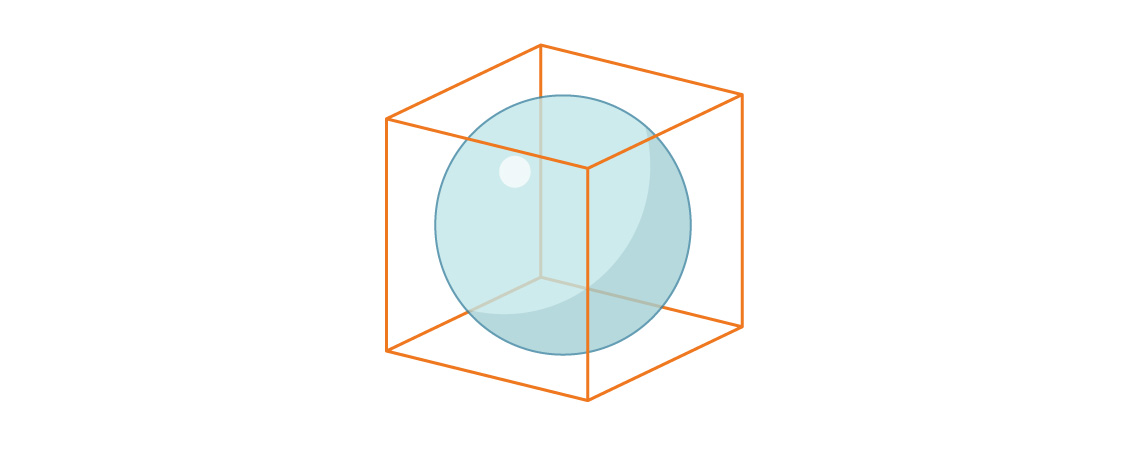
Jari-jari bola juga sama dengan r = 1/2, jadi perbandingan volume bola dengan volume kubus adalah:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

Perhatikan bahwa proporsi kubus yang ditempati oleh bola bertuliskan dalam tiga dimensi lebih kecil dari proporsi persegi yang ditempati oleh lingkaran bertuliskan dalam dua dimensi. Pola ini berlanjut: dengan bertambahnya dimensi, rasio ini menurun. Ketika n tumbuh, bola berdimensi-n menempati ruang berdimensi n semakin sedikit.



Ini dapat ditunjukkan dengan menggunakan aljabar, tetapi juga dapat dipahami jika Anda memikirkan tentang sudut. Dalam dimensi apa pun, bola berdimensi-n dapat dituliskan menjadi kubus berdimensi-n. Bola menyentuh tepi kubus tetapi tidak mencapai sudutnya, jadi ada wilayah di sekitar setiap sudut yang berada di dalam kubus tetapi di luar bola. Namun, kotak berdimensi-n akan memiliki 2 ⁿsudut, yaitu, dengan peningkatan n, jumlah area yang tidak tercakup oleh bola bertambah secara eksponensial. Selain itu, jarak antara sudut dan bola juga bertambah. Ini berarti bahwa dalam jangka panjang, ruang di dalam kubus berdimensi-n, tetapi di luar bola berdimensi-n, hanya akan menghancurkan ruang yang ditempati oleh bola tersebut.



Jika kontraksi bola tampak cukup aneh bagi Anda, maka ahli matematika yang terlibat dalam pengemasan bola memperhatikan sesuatu yang bahkan lebih tidak terduga di dimensi 8 dan 24. Dalam dimensi ini, bola menyusut cukup untuk dapat mengisi celah antara bola baru, yang memberikan kemasan ultra padat di dimensi ini ... Sebuah hipotesis diajukan tentang optimalitas metode khusus ini, tetapi tidak diketahui secara pasti hingga 2016, ketika Marina Vyazovskaya membuktikan teorema ini.untuk ruang 8 dimensi. Seminggu kemudian, Vyazovskaya dan asistennya memperluas metodenya untuk membuktikan kasus ruang 24 dimensi juga.



Berdasarkan penelitian Vyazovskaya bahwa sekarang kita mengetahui cara pengemasan bola yang paling efisien dalam dimensi 1, 2, 3, 8, dan 24. Namun di dimensi lain, masih banyak pekerjaan yang harus dilakukan. Jadi keluarkan jeruk dan kaleng soda dan mulailah bereksperimen. Anda mungkin orang yang bisa mengisi celah penting.

Latihan

1. Katakanlah kita mulai mengemas bidang koordinat seperti yang ditunjukkan pada gambar di bawah. Pusat lingkaran kiri bawah terletak di titik (0, 0), dan pusat lingkaran kanan bawah berada di titik (2, 0).







Dimana pusat lingkaran ketiga?



2. Di bawah ini adalah awal dari pengemasan bola "kubik sederhana". Berapa kepadatan pengepakan dari skema semacam itu?







3. Di sinilah awal pengemasan pesawat menjadi oktagon biasa.







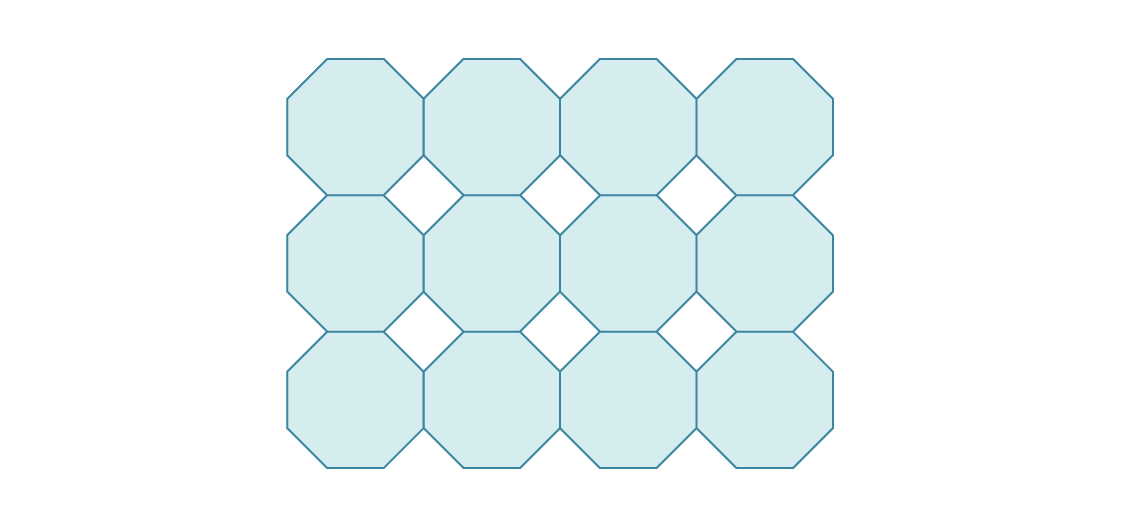
Berapa kepadatan paket seperti itu?

Jawaban

Lihat juga:

• " Google Merilis Sodar - Alat AR untuk Menampilkan Jarak Sosial "
• " Studi meta mengungkapkan keefektifan masker dan menjaga jarak terhadap SARS-CoV-2 (COVID-19) "
• " COVID-19: Model Prediksi Parametrik Epidemi "