
Halo semuanya, hari ini kita akan membahas algoritma kompresi JPEG. Banyak orang tidak tahu bahwa JPEG bukanlah format sebagai algoritma. Sebagian besar gambar JPEG yang Anda lihat ada dalam JFIF (JPEG File Interchange Format), di dalamnya algoritma kompresi JPEG diterapkan. Di akhir artikel, Anda akan memiliki pemahaman yang jauh lebih baik tentang bagaimana algoritma ini mengompresi data dan bagaimana menulis kode pembongkaran dengan Python. Kami tidak akan mempertimbangkan semua nuansa format JPEG (misalnya, pemindaian progresif), tetapi hanya akan berbicara tentang kemampuan dasar format saat kami menulis dekoder kami sendiri.
pengantar
Mengapa menulis artikel lain di JPEG ketika ratusan artikel telah ditulis tentang itu? Biasanya dalam artikel seperti itu, penulis hanya membahas tentang apa formatnya saja. Anda tidak menulis kode unpacking dan decoding. Dan jika Anda menulis sesuatu, itu akan menggunakan C / C ++, dan kode ini tidak akan tersedia untuk banyak orang. Saya ingin mematahkan tradisi ini dan menunjukkan kepada Anda dengan Python 3 cara kerja dekoder JPEG dasar. Ini akan didasarkan pada kode ini yang dikembangkan oleh MIT, tetapi saya akan banyak mengubahnya demi keterbacaan dan kejelasan. Anda dapat menemukan kode yang dimodifikasi untuk artikel ini di repositori saya .
Bagian berbeda dari JPEG
Mari kita mulai dengan gambar yang dibuat oleh Ange Albertini . Ini mencantumkan semua bagian dari file JPEG sederhana. Kami akan menganalisis setiap segmen, dan saat Anda membaca artikelnya, Anda akan kembali ke ilustrasi ini lebih dari sekali.
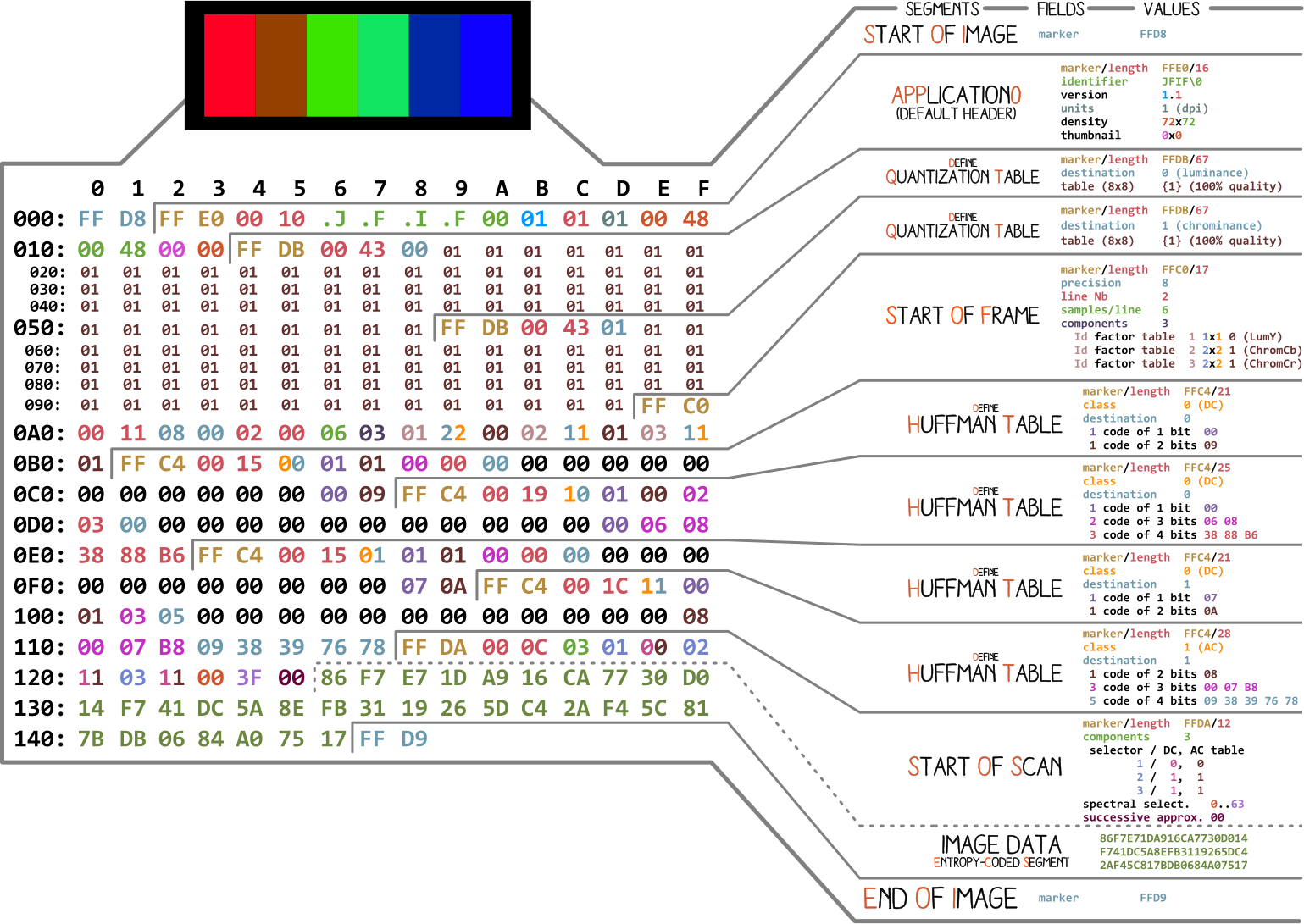
Hampir setiap file biner berisi banyak penanda (atau tajuk). Anda dapat menganggapnya sebagai semacam penanda. Mereka penting untuk bekerja dengan file dan digunakan oleh program seperti file (di Mac dan Linux) sehingga kami dapat mengetahui detail file tersebut. Penanda menunjukkan dengan tepat di mana informasi tertentu disimpan dalam file. Paling sering, penanda ditempatkan sesuai dengan nilai panjang (
length) dari segmen tertentu.
Awal dan akhir file
Penanda pertama yang penting bagi kami adalah
FF D8. Ini mendefinisikan awal gambar. Jika kita tidak menemukannya, maka kita dapat berasumsi bahwa marker tersebut ada di file lain. Penanda tidak kalah pentingnya FF D9. Dikatakan bahwa kami telah mencapai akhir dari file gambar. Setelah setiap penanda, dengan pengecualian rentang FFD0- FFD9dan FF01, segera muncul nilai panjang segmen penanda ini. Dan penanda awal dan akhir file selalu sepanjang dua byte.
Kami akan bekerja dengan gambar ini:

Mari tulis beberapa kode untuk menemukan penanda awal dan akhir.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Untuk membongkar byte gambar, kami menggunakan struct .
>Hmemerintahkannya structuntuk membaca tipe data unsigned shortdan mengerjakannya dalam urutan dari tinggi ke rendah (big-endian). Data JPEG disimpan dalam format tertinggi hingga terendah. Hanya data EXIF yang bisa dalam format little-endian (meskipun biasanya tidak demikian). Dan ukurannya short2, jadi kami mentransfer dari unpackdua byte img_data. Bagaimana kita tahu apa itu short? Kita tahu bahwa penanda dalam JPEG dilambangkan dengan empat karakter heksadesimal: ffd8. Satu karakter seperti itu setara dengan empat bit (setengah byte), jadi empat karakter akan setara dengan dua byte, sama seperti short.
Setelah bagian Mulai Pemindaian, data gambar yang dipindai segera mengikuti, yang tidak memiliki panjang tertentu. Mereka berlanjut sampai akhir penanda file, jadi untuk saat ini kita “mencari” secara manual ketika kita menemukan penanda Start of Scan.
Sekarang mari kita berurusan dengan data gambar lainnya. Untuk melakukan ini, pertama kita mempelajari teorinya, dan kemudian beralih ke pemrograman.
Pengkodean JPEG
Pertama, mari kita bicara tentang konsep dasar dan teknik pengkodean yang digunakan dalam JPEG. Dan pengkodean akan dilakukan dalam urutan terbalik. Dalam pengalaman saya, decoding akan sulit diketahui tanpanya.
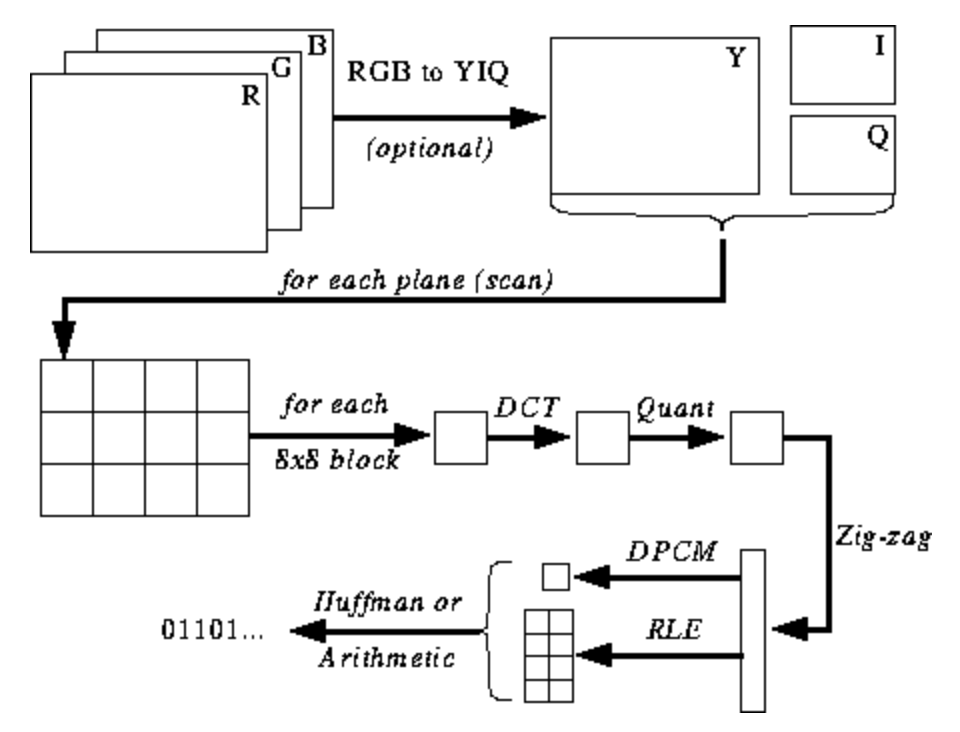
Ilustrasi di bawah ini belum jelas bagi Anda, tetapi saya akan memberi Anda petunjuk saat Anda mempelajari proses encoding dan decoding. Berikut langkah-langkah untuk encoding JPEG ( sumber ):
Ruang warna JPEG
Menurut spesifikasi JPEG ( ISO / IEC 10918-6: 2013 (E) Bagian 6.1):
- Gambar yang dikodekan dengan hanya satu komponen diperlakukan sebagai data skala abu-abu, di mana 0 adalah hitam dan 255 putih.
- Gambar yang dikodekan dengan tiga komponen dianggap sebagai data RGB yang dikodekan dalam ruang YCbCr. Jika gambar berisi segmen penanda APP14 yang dijelaskan dalam Bagian 6.5.3, maka kode warna dianggap RGB atau YCbCr menurut informasi di segmen penanda APP14. Hubungan antara RGB dan YCbCr didefinisikan sesuai dengan ITU-T T.871 | ISO / IEC 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
Sebagian besar implementasi algoritma JPEG menggunakan pencahayaan dan chrominance (pengkodean YUV), bukan RGB. Ini sangat berguna karena mata manusia sangat buruk dalam membedakan perubahan kecerahan frekuensi tinggi di area kecil, sehingga Anda dapat mengurangi frekuensi dan orang tersebut tidak akan melihat perbedaannya. Apa fungsinya? Gambar yang sangat terkompresi dengan penurunan kualitas yang hampir tidak terlihat.
Seperti dalam RGB, setiap piksel dikodekan dengan tiga byte warna (merah, hijau dan biru), jadi di YUV, tiga byte digunakan, tetapi artinya berbeda. Komponen Y mendefinisikan luminansi warna (luminansi, atau luma). U dan V menentukan warna (chroma): U bertanggung jawab atas bagian biru, dan V untuk bagian merah.
Format ini dikembangkan pada saat televisi belum begitu umum, dan para insinyur ingin menggunakan format pengkodean gambar yang sama untuk penyiaran televisi berwarna dan hitam-putih. Baca lebih lanjut tentang ini di sini .
Transformasi dan kuantisasi kosinus diskrit
JPEG mengubah gambar menjadi blok piksel 8x8 (disebut MCU, Unit Pengkodean Minimum), mengubah rentang nilai piksel sehingga pusatnya adalah 0, kemudian menerapkan transformasi kosinus diskrit ke setiap blok dan mengompresi hasilnya menggunakan kuantisasi. Mari kita lihat apa artinya semua ini.
Discrete cosine transform (DCT) adalah metode untuk mengubah data diskrit menjadi kombinasi gelombang kosinus. Mengubah gambar menjadi satu set cosinus tampak seperti latihan yang sia-sia pada pandangan pertama, tetapi Anda akan memahami alasannya saat mempelajari langkah selanjutnya. DCT mengambil blok 8x8 piksel dan memberi tahu kita cara mereproduksi blok itu menggunakan matriks fungsi kosinus 8x8. Lebih lengkapnya di sini .
Matriksnya terlihat seperti ini:

Kami menerapkan DCT secara terpisah ke setiap komponen piksel. Hasilnya, kita mendapatkan matriks koefisien 8x8, yang menunjukkan kontribusi dari masing-masing (dari semua 64) fungsi cosinus dalam matriks masukan 8x8. Dalam matriks koefisien DCT, nilai terbesar biasanya ada di pojok kiri atas, dan yang terkecil ada di kanan bawah. Kiri atas adalah fungsi kosinus frekuensi terendah dan kanan bawah adalah yang tertinggi.
Ini berarti bahwa di sebagian besar gambar terdapat sejumlah besar informasi frekuensi rendah dan sebagian kecil informasi frekuensi tinggi. Jika komponen kanan bawah dari setiap matriks DCT diberi nilai 0, maka gambar yang dihasilkan akan terlihat sama untuk kita, karena seseorang tidak dapat membedakan perubahan frekuensi tinggi dengan buruk. Inilah yang akan kita lakukan di langkah selanjutnya.
Saya menemukan video yang bagus tentang topik ini. Lihat jika Anda tidak mengerti arti PrEP:
Kita semua tahu bahwa JPEG adalah algoritma kompresi lossy. Namun sejauh ini kami belum kehilangan apapun. Kami hanya memiliki blok komponen YUV 8x8 yang diubah menjadi blok fungsi kosinus 8x8 tanpa kehilangan informasi. Tahap kehilangan data adalah kuantisasi.
Kuantisasi adalah proses ketika kita mengambil dua nilai dari kisaran tertentu dan mengubahnya menjadi nilai diskrit. Dalam kasus kami, ini hanyalah nama licik untuk mengurangi ke 0 koefisien frekuensi tertinggi dalam matriks DCT yang dihasilkan. Saat menyimpan gambar menggunakan JPEG, sebagian besar editor grafis menanyakan tingkat kompresi yang ingin Anda atur. Di sinilah hilangnya informasi frekuensi tinggi terjadi. Anda tidak dapat lagi membuat ulang gambar asli dari gambar JPEG yang dihasilkan.
Matriks kuantisasi yang berbeda digunakan tergantung pada rasio kompresi (fakta menarik: sebagian besar pengembang memiliki paten untuk membuat tabel kuantisasi). Kami membagi matriks DCT dari elemen koefisien dengan elemen dengan matriks kuantisasi, membulatkan hasilnya menjadi bilangan bulat dan mendapatkan matriks terkuantisasi.
Mari kita lihat contohnya. Katakanlah ada matriks DCT seperti itu:

Dan inilah matriks kuantisasi yang biasa:
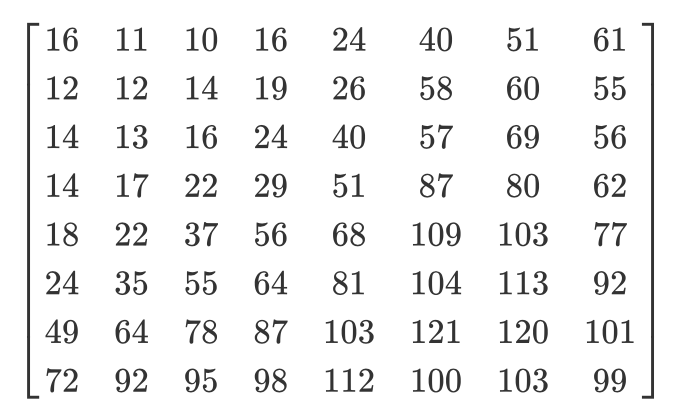
Matriks terkuantisasi akan terlihat seperti ini:

Meskipun manusia tidak dapat melihat informasi frekuensi tinggi, jika Anda menghapus terlalu banyak data dari blok 8x8 piksel, gambar akan terlihat terlalu kasar. Dalam matriks terkuantisasi seperti itu, nilai pertama disebut nilai DC, dan yang lainnya disebut nilai AC. Jika kita mengambil nilai DC dari semua matriks terkuantisasi dan menghasilkan gambar baru, maka kita akan mendapatkan pratinjau dengan resolusi 8 kali lebih kecil dari gambar aslinya.
Saya juga ingin mencatat bahwa karena kita menggunakan kuantisasi, kita perlu memastikan bahwa warnanya berada dalam kisaran [0,255]. Jika mereka terbang keluar, maka Anda harus membawanya secara manual ke kisaran ini.
Zigzag
Setelah kuantisasi, algoritme JPEG menggunakan pemindaian zigzag untuk mengubah matriks menjadi bentuk satu dimensi:
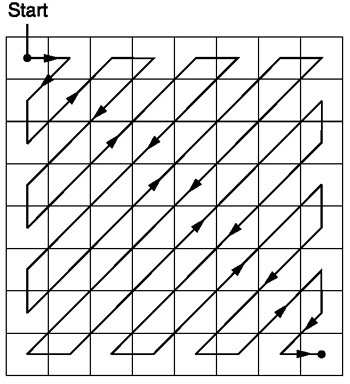
Sumber .
Mari kita memiliki matriks terkuantisasi seperti itu:
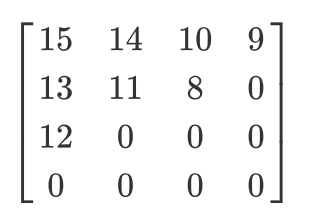
Maka hasil scan zigzag adalah sebagai berikut:
[15 14 13 12 11 10 9 8 0 ... 0]
Pengkodean ini lebih disukai karena setelah kuantisasi, sebagian besar informasi frekuensi rendah (paling penting) akan ditempatkan di awal matriks, dan pemindaian zigzag menyimpan data ini di awal matriks satu dimensi. Ini berguna untuk langkah selanjutnya, kompresi.
Pengkodean run-length dan pengkodean delta
Enkode run-length digunakan untuk mengompresi data berulang. Setelah pemindaian zigzag, kita melihat bahwa sebagian besar ada angka nol di akhir larik. Pengkodean panjang memungkinkan kita memanfaatkan ruang yang terbuang ini dan menggunakan lebih sedikit byte untuk mewakili semua angka nol tersebut. Katakanlah kita memiliki data berikut:
10 10 10 10 10 10 10
Setelah mengkodekan panjang seri, kita mendapatkan ini:
7 10
Kami telah mengompresi 7 byte menjadi 2 byte.
Pengkodean delta digunakan untuk merepresentasikan sebuah byte relatif terhadap byte sebelumnya. Akan lebih mudah untuk menjelaskan dengan sebuah contoh. Mari kita memiliki data berikut:
10 11 12 13 10 9
Menggunakan pengkodean delta, mereka dapat direpresentasikan sebagai berikut:
10 1 2 3 0 -1
Dalam JPEG, setiap nilai DC dari matriks DCT dikodekan dengan delta relatif terhadap nilai DC sebelumnya. Ini berarti bahwa dengan mengubah koefisien DCT pertama pada gambar, Anda akan menghancurkan keseluruhan gambar. Tetapi jika Anda mengubah nilai pertama dari matriks DCT terakhir, maka itu hanya akan memengaruhi fragmen gambar yang sangat kecil.
Pendekatan ini berguna karena nilai DC pertama dari gambar cenderung paling bervariasi, dan dengan pengkodean delta kami membawa nilai DC lainnya mendekati 0, yang meningkatkan kompresi dengan pengkodean Huffman.
Pengkodean Huffman
Ini adalah metode kompresi lossless. Huffman pernah bertanya-tanya, "Berapa jumlah bit terkecil yang dapat saya gunakan untuk menyimpan teks bebas?" Hasilnya, format pengkodean dibuat. Katakanlah kita memiliki teks:
a b c d e
Biasanya, setiap karakter membutuhkan satu byte ruang:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Ini adalah prinsip pengkodean ASCII biner. Bagaimana jika kita mengubah pemetaan?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Kami sekarang membutuhkan lebih sedikit bit untuk menyimpan teks yang sama:
a: 000
b: 001
c: 010
d: 100
e: 011
Itu semua baik dan bagus, tetapi bagaimana jika kita perlu menghemat lebih banyak ruang? Misalnya seperti ini:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
Pengkodean Huffman memungkinkan pencocokan panjang variabel seperti itu. Data masukan diambil, karakter yang paling umum dicocokkan dengan kombinasi bit yang lebih kecil, dan karakter yang lebih jarang - dengan kombinasi yang lebih besar. Dan kemudian hasil pemetaan dikumpulkan menjadi pohon biner. Dalam JPEG, kami menyimpan informasi DCT menggunakan pengkodean Huffman. Ingat saya menyebutkan bahwa pengkodean delta nilai DC membuat pengkodean Huffman lebih mudah? Saya harap Anda sekarang mengerti mengapa. Setelah pengkodean delta, kita perlu mencocokkan lebih sedikit "karakter" dan ukuran pohon dikurangi.
Tom Scott memiliki video bagus yang menjelaskan cara kerja algoritma Huffman. Lihatlah sebelum membaca.
JPEG berisi hingga empat tabel Huffman, yang disimpan di "Define Huffman Table" (dimulai dengan
0xffc4). Koefisien DCT disimpan dalam dua tabel Huffman yang berbeda: dalam satu nilai DC dari tabel zigzag, di sisi lain - nilai AC dari tabel zigzag. Artinya saat melakukan coding, kita perlu menggabungkan nilai DC dan AC dari kedua matriks tersebut. Informasi DCT untuk saluran luma dan kromatisitas disimpan secara terpisah, jadi kami memiliki dua set DC dan dua set informasi AC, total 4 tabel Huffman.
Jika gambar dalam grayscale, maka kita hanya memiliki dua tabel Huffman (satu untuk DC dan satu untuk AC), karena kita tidak membutuhkan warna. Seperti yang mungkin sudah Anda ketahui, dua gambar berbeda dapat memiliki tabel Huffman yang sangat berbeda, jadi penting untuk menyimpannya di dalam setiap JPEG.
Kami sekarang tahu konten utama gambar JPEG. Mari beralih ke decoding.
Pengodean JPEG
Penguraian kode dapat dibagi menjadi beberapa tahap:
- Ekstraksi tabel Huffman dan decoding bit.
- Mengekstrak koefisien DCT menggunakan run-length dan delta coding rollback.
- Menggunakan koefisien DCT untuk menggabungkan gelombang cosinus dan merekonstruksi nilai piksel untuk setiap blok 8x8.
- Ubah YCbCr ke RGB untuk setiap piksel.
- Menampilkan gambar RGB yang dihasilkan.
Standar JPEG mendukung empat format kompresi:
- Mendasarkan
- Serial diperpanjang
- Progresif
- Tidak rugi
Kami akan bekerja dengan kompresi dasar. Ini berisi serangkaian blok 8x8, satu demi satu. Dalam format lain, templat data sedikit berbeda. Untuk memperjelasnya, saya telah mewarnai segmen berbeda dari konten heksadesimal gambar kita:
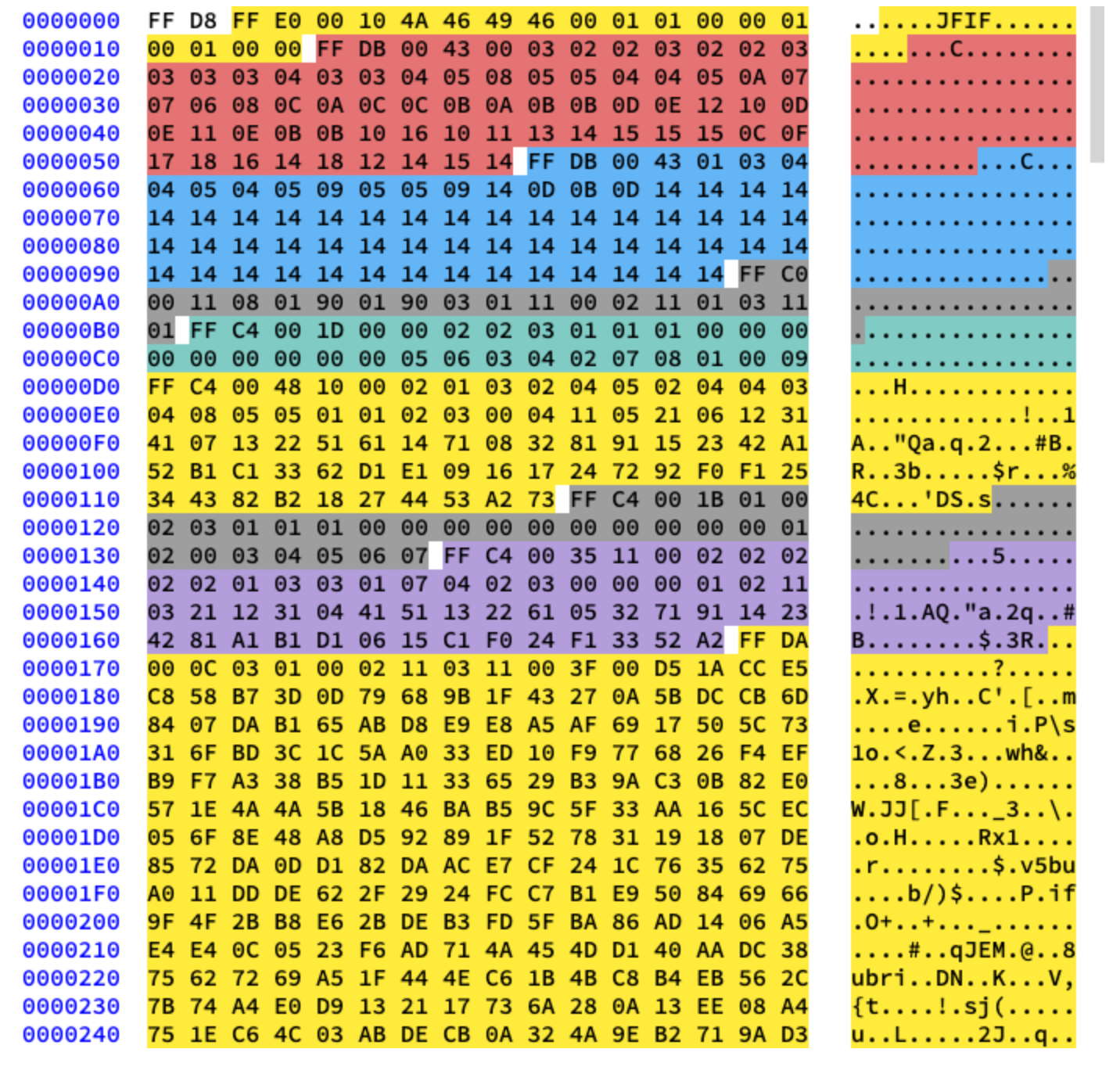
Mengekstrak Tabel Huffman
Kita sudah tahu bahwa JPEG berisi empat tabel Huffman. Ini adalah pengkodean terakhir, jadi kita akan mulai mendekode dengannya. Setiap bagian dengan tabel berisi informasi:
| Bidang | Ukuran | Deskripsi |
|---|---|---|
| ID Penanda | 2 byte | 0xff dan 0xc4 mengidentifikasi DHT |
| Panjangnya | 2 byte | Panjang meja |
| Informasi tabel Huffman | 1 byte | bit 0 ... 3: jumlah tabel (0 ... 3, jika tidak error) bit 4: jenis tabel, 0 = tabel DC, 1 = tabel AC bit 5 ... 7: tidak digunakan, harus 0 |
| Karakter | 16 byte | Jumlah karakter dengan kode panjang 1 ... 16, jumlah (n) byte ini adalah jumlah kode yang harus <= 256 |
| Simbol | n byte | Tabel berisi karakter dalam urutan panjang kode yang bertambah (n = jumlah total kode). |
Katakanlah kita memiliki tabel Huffman seperti ini ( sumber ):
| Simbol | Kode Huffman | Panjang kode |
|---|---|---|
| Sebuah | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| d | 100 | 3 |
| e | 101 | 3 |
| f | 110 | 3 |
| g | 1110 | 4 |
| h | 11110 | lima |
| saya | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | sembilan |
Ini akan disimpan dalam file JFIF seperti ini (dalam format biner. Saya menggunakan ASCII hanya untuk kejelasan):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 berarti kita tidak memiliki kode Huffman dengan panjang 1. A 1 berarti kita memiliki satu kode Huffman dengan panjang 2, dan seterusnya. Di bagian DHT, segera setelah kelas dan ID, data selalu sepanjang 16 byte. Mari tulis kode untuk mengekstrak panjang dan elemen dari DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Setelah menjalankan kode, kami mendapatkan ini:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Luar biasa! Kami memiliki panjang dan elemen. Sekarang Anda perlu membuat kelas tabel Huffman Anda sendiri untuk merekonstruksi pohon biner dari panjang dan elemen yang diperoleh. Saya hanya akan menyalin kodenya dari sini :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitsmengambil panjang dan elemen, mengulang elemen, dan menempatkannya dalam daftar root. Ini adalah pohon biner dan berisi daftar bersarang. Anda dapat membaca di Internet cara kerja pohon Huffman dan cara membuat struktur data seperti itu dengan Python. Untuk DHT pertama kami (dari gambar di awal artikel) kami memiliki data, panjang, dan elemen berikut:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Setelah panggilan selesai,
GetHuffmanBitsdaftar tersebut rootakan berisi data berikut:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTablejuga berisi metode GetCodeyang berjalan melalui pohon dan menggunakan tabel Huffman untuk mengembalikan bit yang didekodekan. Metode ini menerima aliran bit sebagai input - hanya representasi biner dari data. Misalnya, bitstream untuk abcakan menjadi 011000010110001001100011. Pertama, kami mengonversi setiap karakter ke kode ASCII-nya, yang kami ubah menjadi biner. Mari buat kelas untuk membantu mengubah string menjadi bit dan kemudian menghitung bit satu per satu:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Saat menginisialisasi, kami memberikan data biner kelas dan kemudian membacanya menggunakan
GetBitdan GetBitN.
Mendekodekan tabel kuantisasi
Bagian Tentukan Tabel Kuantisasi berisi data berikut:
| Bidang | Ukuran | Deskripsi |
|---|---|---|
| ID Penanda | 2 byte | 0xff dan 0xdb mengidentifikasi bagian DQT |
| Panjangnya | 2 byte | Panjang tabel kuantitas |
| Informasi kuantitas | 1 byte | bit 0 ... 3: jumlah tabel kuantisasi (0 ... 3, jika tidak error) bit 4 ... 7: ketepatan tabel kuantisasi, 0 = 8 bit, sebaliknya 16 bit |
| Byte | n byte | Nilai tabel kuantitas, n = 64 * (presisi + 1) |
Menurut standar JPEG, gambar JPEG default memiliki dua tabel kuantisasi: untuk luma dan chroma. Mereka mulai dengan spidol
0xffdb. Hasil kode kami sudah berisi dua penanda seperti itu. Mari tambahkan kemampuan untuk memecahkan kode tabel kuantisasi:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Kami pertama kali mendefinisikan metode
GetArray. Ini hanyalah teknik yang nyaman untuk mendekode sejumlah variabel byte dari data biner. Kami juga mengganti beberapa kode dalam metode decodeHuffmanuntuk memanfaatkan fungsi baru. Kemudian metode tersebut didefinisikan DefineQuantizationTables: ia membaca judul bagian dengan tabel kuantisasi, dan kemudian menerapkan data kuantisasi ke kamus menggunakan nilai tajuk sebagai kuncinya. nilai ini dapat berupa 0 untuk luminansi dan 1 untuk kromatisitas. Setiap bagian dengan tabel kuantisasi di JFIF berisi 64 byte data (untuk matriks kuantisasi 8x8).
Jika kita mengeluarkan matriks kuantisasi untuk gambar kita, kita mendapatkan ini:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Mendekode awal bingkai
Bagian Start of Frame berisi informasi berikut ( sumber ):
| Bidang | Ukuran | Deskripsi |
|---|---|---|
| ID Penanda | 2 byte | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
Di sini kami tidak tertarik pada semuanya. Kami akan mengekstrak lebar dan tinggi gambar, serta jumlah tabel kuantisasi untuk setiap komponen. Lebar dan tinggi akan digunakan untuk mulai mendekode pindaian gambar yang sebenarnya dari bagian Mulai Pemindaian. Karena kita akan bekerja sebagian besar dengan gambar YCbCr, kita dapat mengasumsikan bahwa akan ada tiga komponen, dan tipenya masing-masing adalah 1, 2 dan 3. Mari tulis kode untuk memecahkan kode data ini:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Kami menambahkan atribut daftar ke kelas JPEG
quantMappingdan mendefinisikan metode BaselineDCTyang menerjemahkan data yang diperlukan dari bagian SOF dan memasukkan jumlah tabel kuantisasi untuk setiap komponen ke dalam daftar quantMapping. Kami akan memanfaatkan ini saat kami mulai membaca bagian Mulai Pindai. Beginilah cara mencari gambar kita quantMapping:
Quant mapping: [0, 1, 1]
Decoding Mulai dari Scan
Ini adalah "daging" dari gambar JPEG, ini berisi data dari gambar itu sendiri. Kami telah mencapai tahap yang paling penting. Segala sesuatu yang kami dekode sebelumnya dapat dianggap sebagai kartu yang membantu kami memecahkan kode gambar itu sendiri. Bagian ini berisi gambar itu sendiri (dikodekan). Kami membaca bagian dan mendekripsi menggunakan data yang sudah diterjemahkan.
Semua penanda dimulai dengan
0xff. Nilai ini juga bisa menjadi bagian dari gambar yang dipindai, tetapi jika ada di bagian ini, akan selalu diikuti oleh dan 0x00. Encoder JPEG memasukkannya secara otomatis, ini disebut dengan byte stuffing. Oleh karena itu, decoder harus menghapus ini 0x00. Mari kita mulai dengan metode dekode SOS yang berisi fungsi seperti itu dan singkirkan yang sudah ada 0x00. Dalam gambar kami di bagian dengan pemindaian tidak ada0xfftapi itu masih merupakan tambahan yang berguna.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Sebelumnya, kami mencari akhir file secara manual ketika kami menemukan penanda
0xffda, tetapi sekarang kami memiliki alat yang memungkinkan kami untuk melihat seluruh file secara sistematis, kami akan memindahkan kondisi pencarian penanda di dalam operator else. Fungsi RemoveFF00hanya berhenti ketika menemukan sesuatu yang lain, bukan 0x00setelahnya 0xff. Perulangan putus saat fungsi menemukan 0xffd9, sehingga kita dapat mencari akhir file tanpa takut kejutan. Jika Anda menjalankan kode ini, Anda tidak akan melihat sesuatu yang baru di terminal.
Ingat, JPEG membagi gambar menjadi matriks 8x8. Sekarang kita perlu mengonversi data gambar yang dipindai menjadi bitstream dan memprosesnya dalam potongan 8x8. Mari tambahkan kode ke kelas kita:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Mari kita mulai dengan mengubah data menjadi bitstream. Apakah Anda ingat bahwa pengkodean delta diterapkan ke elemen DC dari matriks kuantisasi (elemen pertamanya) relatif terhadap elemen DC sebelumnya? Oleh karena itu, kami menginisialisasi
oldlumdccoeff, oldCbdccoeffdan oldCrdccoeffdengan nilai nol, nilai tersebut akan membantu kami melacak nilai elemen DC sebelumnya, dan 0 akan disetel secara default saat kami menemukan elemen DC pertama.
Lingkaran itu
formungkin tampak aneh. self.height//8memberi tahu kita berapa kali kita bisa membagi tinggi dengan 8 8, dan itu sama dengan lebar dan self.width//8.
BuildMatrixakan mengambil tabel kuantisasi dan menambahkan parameter, membuat matriks transformasi kosinus diskrit terbalik dan memberi kita matriks Y, Cr, dan Cb. Dan fungsinya DrawMatrixmengubahnya menjadi RGB.
Pertama, mari buat kelas
IDCT, lalu mulai mengisi metode BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Mari kita menganalisis kelas
IDCT. Saat kami mengekstrak MCU, itu akan disimpan di atribut base. Kemudian kami mengubah matriks MCU dengan memutar kembali pemindaian zigzag menggunakan metode rearrange_using_zigzag. Terakhir, kita akan mengembalikan transformasi diskrit kosinus dengan memanggil metode tersebut perform_IDCT.
Seperti yang Anda ingat, tabel DC sudah diperbaiki. Kami tidak akan mempertimbangkan cara kerja DCT, ini lebih terkait dengan matematika daripada pemrograman. Kami dapat menyimpan tabel ini sebagai variabel global dan kueri untuk pasangan nilai
x,y. Saya memutuskan untuk meletakkan tabel dan perhitungannya di kelas IDCTagar teksnya dapat dibaca. Setiap elemen dari matriks MCU yang ditransformasikan dikalikan dengan nilai idc_variabledan kita mendapatkan nilai Y, Cr, dan Cb.
Ini akan menjadi lebih jelas saat kita menambahkan metode
BuildMatrix.
Jika Anda mengubah tabel zigzag menjadi seperti ini:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
Anda mendapatkan hasil ini (perhatikan artefak kecil):

Dan jika Anda memiliki keberanian, Anda dapat memodifikasi tabel zigzag lebih banyak lagi:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Maka hasilnya akan seperti ini:

Mari selesaikan metode kita
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Kita mulai dengan membuat kelas inversi transformasi kosinus diskrit (
IDCT()). Kemudian kami membaca data ke dalam bitstream dan mendekodekannya menggunakan tabel Huffman.
self.huffman_tables[0]dan self.huffman_tables[1]mengacu pada tabel DC untuk luma dan chroma, masing-masing, dan self.huffman_tables[16]dan self.huffman_tables[17]mengacu pada tabel AC untuk luma dan chroma, masing-masing.
Setelah mendekode bitstream, kami menggunakan fungsi untuk
DecodeNumber mengekstrak koefisien DC berkode-delta baru dan menambahkannya olddccoefficientuntuk mendapatkan koefisien DC yang didekode-delta .
Kami kemudian mengulangi prosedur decoding yang sama dengan nilai AC dalam matriks kuantisasi. Arti kode
0menunjukkan bahwa kita telah mencapai penanda End of Block (EOB) dan harus berhenti. Selain itu, bagian pertama dari tabel kuantisasi AC memberi tahu kita berapa banyak nol di depan yang kita miliki. Sekarang mari kita ingat tentang pengkodean panjang seri. Mari balikkan proses ini dan lewati semua bit itu. IDCTMereka secara eksplisit diberi angka nol di kelas .
Setelah mendekode nilai DC dan AC untuk MCU, kami mengubah MCU dan membalikkan pemindaian zigzag dengan memanggil
rearrange_using_zigzag. Dan kemudian kami membalikkan DCT dan menerapkannya ke MCU yang telah diterjemahkan.
Metode ini
BuildMatrixakan mengembalikan matriks DCT terbalik dan nilai koefisien DC. Ingatlah bahwa ini akan menjadi matriks hanya untuk satu unit pengkodean minimal 8x8. Mari lakukan ini untuk semua MCU lain di file kita.
Menampilkan gambar di layar
Sekarang mari kita buat kode kita dalam metode
StartOfScanmembuat Kanvas Tkinter dan menggambar setiap MCU setelah decoding.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Mari kita mulai dengan fungsi
ColorConversiondan Clamp. ColorConversionmengambil nilai Y, Cr dan Cb, mengonversinya menjadi komponen RGB dengan rumus, dan kemudian mengeluarkan nilai RGB gabungan. Mengapa menambahkan 128 pada mereka, Anda mungkin bertanya? Ingat, sebelum algoritma JPEG, DCT diterapkan ke MCU dan mengurangi 128 dari nilai warna. Jika warna aslinya dalam kisaran [0,255], JPEG akan menempatkannya dalam kisaran [-128, + 128]. Kami perlu memutar kembali efek ini saat mendekode, jadi kami menambahkan 128 ke RGB. Adapun Clamp, saat membongkar, nilai yang dihasilkan mungkin berada di luar kisaran [0,255], jadi kami menyimpannya dalam kisaran ini [0,255].
Dalam metode
DrawMatrixkita mengulang setiap matriks 8x8 yang telah didekode untuk Y, Cr dan Cb, dan mengonversi setiap elemen matriks ke nilai RGB. Setelah bertransformasi, kami menggambar piksel di Tkinter canvasmenggunakan metode ini create_rectangle. Anda dapat menemukan semua kode di GitHub . Jika Anda menjalankannya, wajah saya akan muncul di layar.
Kesimpulan
Siapa sangka untuk menunjukkan wajah saya Anda harus menulis penjelasan lebih dari 6.000 kata. Sungguh menakjubkan betapa pintarnya penulis beberapa algoritme! Semoga Anda menikmati artikelnya. Saya belajar banyak saat menulis decoder ini. Saya tidak berpikir ada begitu banyak matematika yang terlibat dalam pengkodean gambar JPEG sederhana. Lain kali Anda dapat mencoba menulis decoder untuk PNG (atau format lain).
Bahan tambahan
Jika Anda tertarik dengan detailnya, baca materi yang saya gunakan untuk menulis artikel, serta beberapa pekerjaan tambahan:
- Panduan Bergambar untuk JPEG Unraveling
- Artikel yang sangat rinci tentang pengkodean Huffman dalam JPEG
- Menulis Perpustakaan JPEG Sederhana di C ++
- Dokumentasi untuk struct dengan Python 3
- Bagaimana FB memanfaatkan pengetahuan JPEG
- Tata letak dan format JPEG
- Presentasi DoD yang menarik tentang forensik JPEG