
Masalah keamanan informasi memerlukan studi dan solusi dari sejumlah masalah teoritis dan praktis dalam interaksi informasi pelanggan sistem. Doktrin kami tentang keamanan informasi merumuskan tiga tugas untuk memastikan integritas, kerahasiaan, dan ketersediaan informasi. Artikel yang disajikan di sini dikhususkan untuk pertimbangan masalah spesifik solusinya dalam kerangka berbagai sistem negara dan subsistem. Sebelumnya, penulis mempertimbangkan dalam 5 artikel masalah memastikan kerahasiaan pesan dengan menggunakan standar negara. Konsep umum sistem pengkodean juga diberikan oleh saya sebelumnya .
pengantar
Dengan pendidikan dasar saya, saya bukan ahli matematika, tetapi sehubungan dengan disiplin ilmu yang saya baca di universitas, saya harus memahaminya dengan cermat. Untuk waktu yang lama dan terus-menerus saya membaca buku teks klasik Universitas terkemuka kami, ensiklopedia matematika lima jilid, banyak brosur populer tipis tentang masalah tertentu, tetapi kepuasan tidak muncul. Pemahaman bacaan yang dalam juga tidak muncul.
Semua matematika klasik difokuskan, sebagai suatu peraturan, pada kasus teoritis tak hingga, dan disiplin khusus didasarkan pada kasus konstruksi dan struktur matematika yang terbatas. Perbedaan dalam pendekatan sangat besar, tidak adanya atau kurangnya contoh lengkap yang baik mungkin merupakan kelemahan utama dan kurangnya buku teks universitas. Sangat jarang ada buku masalah dengan solusi untuk pemula (untuk mahasiswa baru), dan yang memang ada berdosa dalam kelalaian dalam penjelasan. Secara umum, saya jatuh cinta dengan toko buku teknis bekas, berkat perpustakaannya dan, sampai batas tertentu, gudang pengetahuannya diisi kembali. Saya memiliki kesempatan untuk membaca banyak, banyak, tetapi "tidak pergi".
Jalan ini membawa saya pada pertanyaan, apa yang dapat saya lakukan sendiri tanpa buku "kruk", yang di depan saya hanya memiliki selembar kertas kosong dan pensil dengan penghapus? Ternyata cukup sedikit dan tidak sesuai dengan yang dibutuhkan. Jalan sulit pendidikan mandiri yang sembarangan dilalui. Pertanyaannya adalah ini. Dapatkah saya membuat dan menjelaskan, pertama-tama kepada diri saya sendiri, pekerjaan kode yang mendeteksi dan memperbaiki kesalahan, misalnya, kode Hamming, (7, 4) -code?
Diketahui bahwa kode Hamming digunakan secara luas di banyak aplikasi di bidang penyimpanan dan pertukaran data, terutama di RAID; selain itu, ini ada dalam memori ECC dan memungkinkan koreksi on-the-fly dari kesalahan tunggal dan ganda.
Informasi keamanan. Kode, sandi, pesan steg
Interaksi informasi melalui pertukaran pesan antara pesertanya harus diberikan perlindungan pada tingkat yang berbeda dan dengan berbagai cara, baik perangkat keras maupun perangkat lunak. Alat-alat ini dikembangkan, dirancang dan dibuat dalam kerangka teori tertentu (lihat Gambar A) dan teknologi yang diadopsi oleh perjanjian internasional pada model OSI / ISO.
Perlindungan informasi dalam sistem telekomunikasi informasi (ITS) praktis menjadi masalah utama dalam menyelesaikan masalah manajemen, baik pada skala individu - pengguna, dan untuk perusahaan, asosiasi, departemen dan negara secara keseluruhan. Dari semua aspek perlindungan ITKS, dalam artikel ini kami akan mempertimbangkan perlindungan informasi selama ekstraksi, pemrosesan, penyimpanan, dan transmisi dalam sistem komunikasi.
Lebih lanjut memperjelas bidang subjek, kami akan fokus pada dua arah yang mungkin, di mana dua pendekatan berbeda untuk perlindungan, presentasi dan penggunaan informasi dipertimbangkan: sintaksis dan semantik. Angka tersebut menggunakan singkatan: codec - codec - decoder; shidesh - decoder-decoder; pekikan - concealer - ekstraktor.
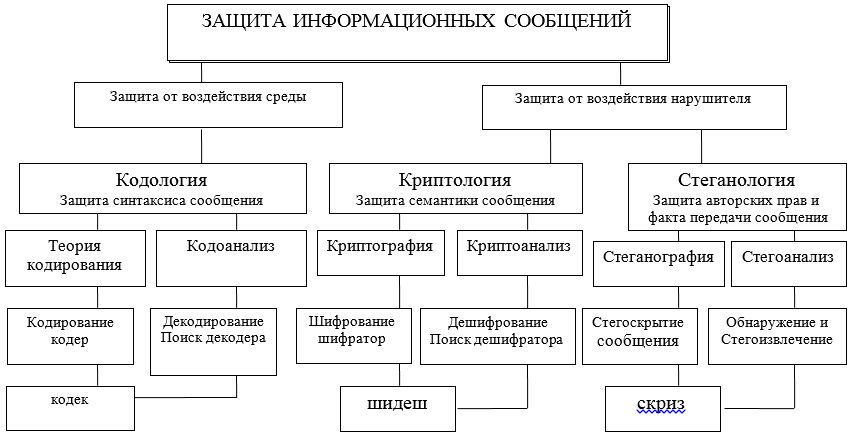
Gambar A - Diagram arah utama dan keterkaitan teori yang bertujuan untuk memecahkan masalah perlindungan interaksi informasi
Fitur sintaksis dari penyajian pesan memungkinkan Anda untuk mengontrol dan memastikan kebenaran dan keakuratan (bebas kesalahan, integritas) dari presentasi selama penyimpanan, pemrosesan, dan terutama saat mengirimkan informasi melalui saluran komunikasi. Di sini, masalah utama perlindungan diselesaikan dengan metode kodologi, sebagian besar - teori kode koreksi.
Keamanan semantik (semantik)pesan disediakan dengan metode kriptologi, yang melalui kriptografi memungkinkan untuk melindungi calon penyusup dari penguasaan konten informasi. Dalam hal ini, pelanggar dapat menyalin, mencuri, mengubah atau mengganti, atau bahkan menghancurkan pesan dan pembawanya, tetapi dia tidak akan dapat memperoleh informasi tentang konten dan makna pesan yang dikirimkan. Isi informasi dalam pesan tersebut akan tetap tidak dapat diakses oleh pelanggar. Dengan demikian, subjek pertimbangan lebih lanjut adalah perlindungan sintaksis dan semantik informasi di ITCS. Pada artikel ini, kami akan membatasi diri untuk hanya mempertimbangkan pendekatan sintaksis dalam implementasi yang sederhana, tetapi sangat penting dengan mengoreksi kode.
Saya akan segera menarik garis pemisah dalam memecahkan masalah keamanan informasi:
teori kodologidirancang untuk melindungi informasi (pesan) dari kesalahan (perlindungan dan analisis sintaks pesan) saluran dan lingkungan, untuk mendeteksi dan memperbaiki kesalahan;
teori kriptologi dirancang untuk melindungi informasi dari akses tidak sah ke semantiknya oleh penyusup (perlindungan semantik, arti pesan);
teori steganologi dirancang untuk melindungi fakta pertukaran informasi pesan, serta untuk melindungi hak cipta, data pribadi (perlindungan kerahasiaan medis).
Secara umum, ayo pergi. Menurut definisi, dan jumlahnya cukup banyak, sangat sulit untuk memahami bahwa ada kode. Penulis menulis bahwa kode tersebut adalah algoritma, tampilan, dan sesuatu yang lain. Saya tidak akan menulis tentang klasifikasi kode di sini, saya hanya akan mengatakan bahwa kode (7, 4) adalah blok .
Pada titik tertentu, saya sadar bahwa kode itu adalah kata-kata kode khusus, sekumpulan terbatas darinya, yang digantikan oleh algoritme khusus dengan teks asli dari pesan di sisi transmisi saluran komunikasi dan yang dikirim melalui saluran ke penerima. Penggantian dilakukan oleh perangkat encoder, dan di sisi penerima kata-kata ini dikenali oleh perangkat decoder.
Karena peran para pihak dapat diubah, kedua perangkat ini digabungkan menjadi satu dan disingkat codec (encoder / decoder), dan dipasang di kedua ujung saluran. Selanjutnya, karena ada kata, ada juga alfabet. Alfabet terdiri dari dua karakter {0, 1}, biner blokkode. Alfabet bahasa alami (NL) adalah sekumpulan simbol - huruf yang menggantikan bunyi ucapan lisan saat menulis. Di sini kita tidak akan mempelajari tulisan hieroglif dalam tulisan suku kata atau nodular.
Alfabet dan kata-kata sudah menjadi bahasa, diketahui bahwa bahasa alami manusia itu mubazir, tetapi artinya, di mana redundansi bahasa tinggal sulit untuk dikatakan, redundansi tidak terorganisir dengan baik, kacau. Saat membuat kode, menyimpan informasi, mereka cenderung mengurangi redundansi, misalnya, pengarsip, kode Morse, dll.
Richard Hemming mungkin menyadari lebih awal dari yang lain bahwa jika redundansi tidak dihilangkan, tetapi cukup teratur, maka itu dapat digunakan dalam sistem komunikasi untuk mendeteksi kesalahan dan secara otomatis memperbaikinya dalam kata sandi dari teks yang ditransmisikan. Dia menyadari bahwa semua 128 kata biner tujuh-bit dapat digunakan untuk mendeteksi kesalahan dalam kata sandi yang membentuk sebuah kode - bagian dari 16 kata biner tujuh-bit. Itu adalah tebakan yang brilian.
Sebelum ditemukannya Hamming, kesalahan juga terdeteksi oleh pihak penerima ketika teks yang diterjemahkan tidak dapat dibaca atau ternyata tidak sesuai dengan yang dibutuhkan. Dalam hal ini, permintaan dikirim ke pengirim pesan untuk mengulangi blok kata-kata tertentu, yang, tentu saja, sangat merepotkan dan memperlambat sesi komunikasi. Ini adalah masalah besar yang tidak terpecahkan selama beberapa dekade.
Pembuatan kode Hamming (7, 4)
Mari kembali ke Hamming. Kata-kata kode (7, 4) terbentuk dari 7 bit j =, j = 0 (1) 15, simbol 4-informasi dan 3-centang, yaitu pada dasarnya berlebihan, karena mereka tidak membawa informasi pesan. Dimungkinkan untuk merepresentasikan tiga digit cek ini dengan fungsi linier dari 4 simbol informasi di setiap kata, yang memastikan deteksi fakta kesalahan dan tempatnya dalam kata-kata untuk membuat koreksi. A (7, 4) -code mendapat kata sifat baru dan menjadi biner blok linier .
Dependensi fungsional linier (aturan (*)) untuk menghitung nilai simbol
terlihat seperti ini:
Memperbaiki kesalahan menjadi operasi yang sangat sederhana - karakter (nol atau satu) ditentukan dalam bit yang salah dan diganti dengan kebalikan lain 0 oleh 1 atau 1 dengan 0.
Berapa banyak kata berbeda yang membentuk kode? Jawaban atas pertanyaan untuk kode (7, 4) ini sangat sederhana. Karena hanya ada 4 digit informasi, dan ragamnya, bila diisi dengan simbol, memiliki= 16 opsi, maka tidak ada kemungkinan lain, yaitu kode yang hanya terdiri dari 16 kata memastikan bahwa 16 kata ini mewakili keseluruhan tulisan dari seluruh bahasa.
Bagian informasi dari 16 kata ini diberi nomor #
():
0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100;
1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101;
2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110;
3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111.
Masing-masing kata 4-bit ini perlu dihitung dan ditambahkan ke kanan dengan 3 bit cek, yang dihitung menurut aturan (*). Misalnya untuk kata informasi No. 6 sama dengan 0110, kita punya dan mengevaluasi karakter centang memberikan hasil berikut untuk kata ini:
Dalam hal ini, kata kode keenam mengambil bentuk: Dengan cara yang sama perlu untuk menghitung simbol cek untuk semua 16 codeword. Mari siapkan tabel 16-baris K untuk kata-kata kode dan isi selnya secara berurutan (saya sarankan pembaca untuk melakukan ini dengan pensil di tangan).
Tabel K - kata sandi j, j = 0 (1) 15, (7, 4) - kode Hamming
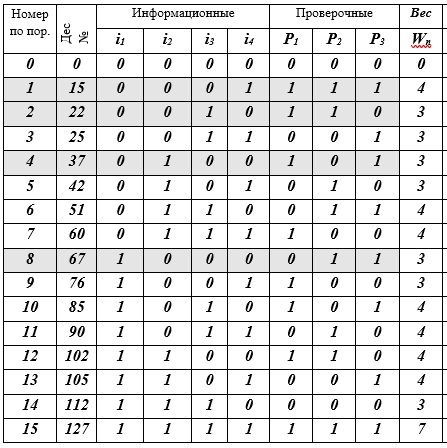
Deskripsi tabel: 16 baris - kata kode; 10 kolom: nomor urut, representasi desimal dari codeword, 4 simbol informasi, 3 simbol cek, W-weight dari codeword sama dengan jumlah bit bukan-nol (≠ 0). 4 kode kata-baris disorot dengan mengisi - ini adalah dasar dari subruang vektor. Sebenarnya, itu saja - kodenya dibuat.
Jadi, tabel tersebut berisi semua kata (7, 4) - kode Hamming. Seperti yang Anda lihat, itu tidak terlalu sulit. Selanjutnya, kita akan berbicara tentang ide apa yang membawa Hamming ke konstruksi kode ini. Kita semua akrab dengan kode Morse, dengan alfabet semaphore angkatan laut dan sistem lain yang dibangun di atas prinsip heuristik yang berbeda, tetapi di sini di (7, 4) -kode, prinsip dan metode matematika yang ketat digunakan untuk pertama kalinya. Ceritanya hanya tentang mereka.
Dasar matematika dari kode. Aljabar yang lebih tinggi
Waktunya telah tiba untuk menceritakan bagaimana R. Hemming mendapatkan ide untuk membuka kode semacam itu. Dia tidak memiliki ilusi khusus tentang bakatnya dan dengan sederhana merumuskan tugas untuk dirinya sendiri: membuat kode yang akan mendeteksi dan memperbaiki satu kesalahan di setiap kata (pada kenyataannya, bahkan dua kesalahan terdeteksi, tetapi hanya satu yang diperbaiki). Dengan saluran berkualitas, bahkan satu kesalahan adalah peristiwa langka. Oleh karena itu, rencana Hemming masih muluk pada skala sistem komunikasi. Ada revolusi dalam teori pengkodean setelah dipublikasikan.
Saat itu tahun 1950. Di sini saya memberikan deskripsi saya yang sederhana (saya harap, dapat dimengerti), yang belum pernah saya lihat dari penulis lain, tetapi ternyata, semuanya tidak sesederhana itu. Dibutuhkan pengetahuan dari berbagai bidang matematika dan waktu untuk memahami segalanya dan memahami sendiri mengapa hal itu dilakukan dengan cara ini. Hanya setelah itu saya dapat menghargai ide indah dan cukup sederhana yang diterapkan dalam kode koreksi ini. Sebagian besar waktu saya habiskan untuk berurusan dengan teknik perhitungan dan pembenaran teoretis dari semua tindakan yang saya tulis di sini.
Pencipta kode, untuk waktu yang lama, tidak dapat memikirkan kode yang mendeteksi dan mengoreksi dua kesalahan. Ide-ide yang digunakan oleh Hemming tidak berhasil di sana. Saya harus melihat, dan ide-ide baru ditemukan. Sangat menarik! Memikat. Butuh waktu sekitar 10 tahun untuk menemukan ide-ide baru, dan baru setelah itu ada terobosan. Kode yang menunjukkan jumlah kesalahan yang sewenang-wenang diterima relatif cepat.
Ruang vektor, bidang, dan grup . Hasil (7, 4) -code (Tabel K) mewakili satu set codeword yang merupakan elemen dari subruang vektor (dari urutan 16, dengan dimensi 4), yaitu bagian dari ruang vektor dimensi 7 dengan urutanDari 128 kata tersebut, hanya 16 yang dimasukkan dalam kode, namun dimasukkan ke dalam kode karena suatu alasan.
Pertama, mereka adalah subruang dengan semua properti dan singularitas berikutnya; kedua, codeword adalah subgrup dari grup besar orde 128, terlebih lagi, subgrup aditif dari bidang Galois yang diperluas hingga GF () derajat pemuaian n = 7 dan karakteristik 2. Subkelompok besar ini didekomposisi menjadi kelas-kelas yang berdekatan oleh subkelompok yang lebih kecil, yang diilustrasikan dengan baik oleh tabel D. Tabel ini dibagi menjadi dua bagian: atas dan bawah, tetapi harus dibaca sebagai satu kelompok panjang. Setiap kelas yang berdekatan (baris tabel) adalah elemen dari kelompok faktor dengan persamaan komponen.
Tabel D - Penguraian kelompok aditif dari bidang Galois GF () menjadi coset (baris Tabel D) untuk subgrup orde 16.
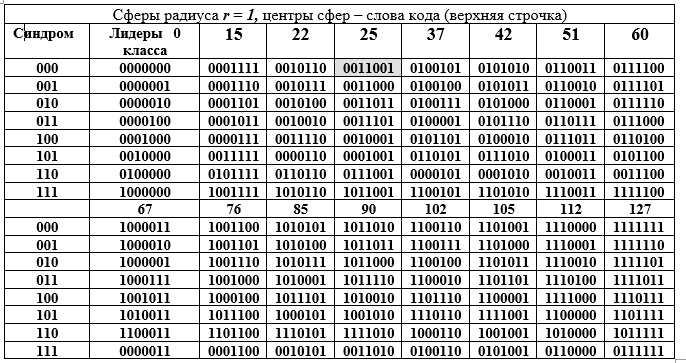
Kolom tabel adalah bola radius 1. Kolom kiri (berulang) adalah sindrom kata (7, 4) kode Hamming, kolom berikutnya adalah pemimpin kelas yang berdekatan. Mari kita buka representasi biner dari salah satu elemen (yang ke-25 disorot dengan mengisi) dari kelompok faktor dan representasi desimalnya:
Teknik memperoleh baris tabel D. Sebuah elemen dari kolom pemimpin kelas dijumlahkan dengan setiap elemen dari header kolom tabel D (penjumlahan dilakukan untuk baris pemimpin dalam bentuk biner mod2). Karena semua ketua kelas memiliki bobot W = 1, maka semua penjumlahan berbeda dari kata pada heading kolom hanya pada satu posisi (sama untuk seluruh baris, tetapi berbeda untuk kolom). Tabel D memiliki interpretasi geometris yang luar biasa. Semua 16 codeword diwakili oleh pusat-pusat bola di ruang vektor 7-dimensi. Semua kata dalam kolom berbeda dengan kata atas pada posisi yang sama, yaitu terletak pada permukaan bola dengan jari-jari r = 1.
Interpretasi ini menyembunyikan gagasan untuk mendeteksi satu kesalahan dalam kata kode apa pun. Kami bekerja dengan bidang. Kondisi pertama untuk deteksi kesalahan adalah bahwa bidang dengan radius 1 tidak boleh bersentuhan atau berpotongan. Ini berarti bahwa pusat bola berada pada jarak 3 atau lebih dari satu sama lain. Dalam hal ini, bola tidak hanya tidak berpotongan, tetapi juga tidak saling bersentuhan. Ini adalah persyaratan untuk ketidakjelasan keputusan: bidang apa yang harus dikaitkan dengan kata yang salah yang diterima di sisi penerima oleh decoder (bukan kode salah satu dari 128 -16 = 112).
Kedua, seluruh kumpulan kata biner 7-bit yang terdiri dari 128 kata didistribusikan secara merata di 16 bidang. Dekoder hanya bisa mendapatkan satu kata dari kumpulan 128 kata yang dikenal ini dengan atau tanpa kesalahan. Ketiga, sisi penerima dapat menerima kata tanpa kesalahan atau dengan distorsi, tetapi selalu termasuk dalam salah satu dari 16 bidang, yang dengan mudah ditentukan oleh decoder. Dalam situasi terakhir, keputusan dibuat bahwa kata kode dikirim - pusat bola ditentukan oleh decoder, yang menemukan posisi (persimpangan baris dan kolom) kata dalam tabel D, yaitu nomor kolom dan baris.
Di sini, persyaratan muncul untuk kata-kata dalam kode dan untuk kode secara keseluruhan: jarak antara dua kata sandi harus setidaknya tiga, yaitu, perbedaan untuk sepasang kata sandi, misalnya, Ci = 85 == 1010101; j = 25 == 0011001 minimal harus 3; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, bobot selisih kata W (76) = 3. (Tabel D menggantikan kalkulasi selisih dan penjumlahan). Di sini, jarak antara vektor kata biner dipahami sebagai jumlah posisi yang tidak cocok dalam dua kata. Ini adalah jarak Hamming, yang telah digunakan secara luas dalam teori dan praktik, karena ia memenuhi semua aksioma jarak.
Komentar . Kode (7, 4) bukan hanya kode biner blok linier , tetapi juga merupakan kode grup , yaitu kata-kata dari kode tersebut membentuk grup aljabar dengan penambahan. Ini berarti bahwa dua codeword, jika ditambahkan bersama, akan memberikan salah satu codeword. Hanya ini bukan operasi penjumlahan biasa, ini adalah penjumlahan modulo dua.
Tabel E - Jumlah elemen grup (codeword) yang digunakan untuk membuat kode Hamming
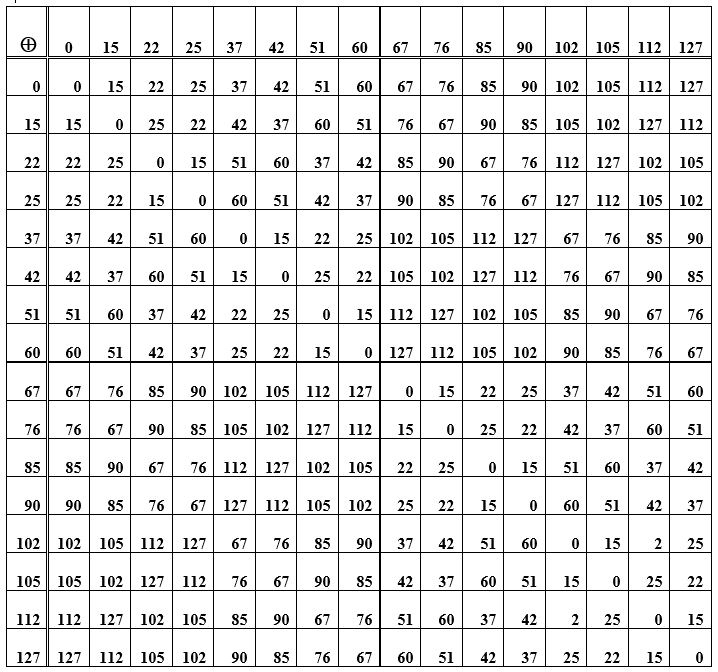
Operasi penjumlahan kata itu sendiri bersifat asosiatif, dan untuk setiap elemen dalam kumpulan kata sandi ada kebalikannya, yaitu menjumlahkan kata asli dengan kebalikannya memberikan nilai nol. Kata sandi nol ini adalah elemen netral dalam grup. Dalam tabel D, ini adalah diagonal utama dari nol. Sel lainnya (perpotongan baris / kolom) merupakan representasi angka-desimal dari kata kode yang diperoleh dengan menjumlahkan elemen dari baris dan kolom. Saat Anda menyusun ulang kata di tempat (saat menambahkan), hasilnya tetap sama, apalagi pengurangan dan penambahan kata memiliki hasil yang sama. Selanjutnya, sistem encoding / decoding yang mengimplementasikan prinsip sindromik dipertimbangkan.
Aplikasi kode. Pembuat kode
Encoder terletak di sisi transmisi saluran dan digunakan oleh pengirim pesan. Pengirim pesan (penulis) membentuk pesan dalam alfabet bahasa alami dan menyajikannya dalam bentuk digital. (Nama karakter dalam kode ASCII dan biner).
Lebih mudah membuat teks dalam file untuk PC menggunakan keyboard standar (kode ASCII). Setiap karakter (huruf alfabet) sesuai dengan satu oktet bit (delapan bit) dalam pengkodean ini. Untuk kode (7, 4) - Hamming yang kata-katanya hanya terdapat 4 simbol informasi, pada saat melakukan pengkodean simbol keyboard menjadi huruf, diperlukan dua kata kode, yaitu. oktet surat dipecah menjadi dua kata informasi dari bahasa alami (NL) dari bentuk
...
Contoh 1 . Anda perlu mentransfer kata "digit" ke NL. Kami memasukkan tabel kode ASCII, huruf-hurufnya sesuai dengan: c –11110110, dan –11101000, f - 11110100, p - 11110000, dan - 11100000 oktet. Atau sebaliknya, dalam kode ASCII, kata "digit" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000
dengan pengelompokan menjadi tetrad (masing-masing 4 digit). Jadi, pengkodean kata "digit" NL membutuhkan 10 kata kode dari (7, 4) kode Hamming. Tetrad mewakili bit informasional dari kata-kata pesan. Kata-kata informasi ini (tetrad) diubah menjadi kata-kata kode (masing-masing 7 bit) sebelum dikirim ke saluran jaringan komunikasi. Hal ini dilakukan dengan perkalian vektor-matriks: kata informasi dengan matriks pembangkitan. Pembayaran untuk kenyamanan sangat mahal dan memakan waktu, tetapi semuanya bekerja secara otomatis dan, yang terpenting, pesan dilindungi dari kesalahan.
Matriks pembangkitan kode Hamming (7, 4) atau generator kata kode diperoleh dengan menuliskan vektor basis dari kode dan menggabungkannya menjadi matriks. Ini mengikuti dari teorema aljabar linier: setiap vektor ruang (subruang) adalah kombinasi linier dari vektor basis, yaitu independen linier di ruang ini. Inilah yang diperlukan - untuk menghasilkan vektor apa pun (kata kode 7-bit) dari informasi yang 4-bit.
Matriks pembangkitan kode hamming (7, 4, 3) atau code word generator berupa:
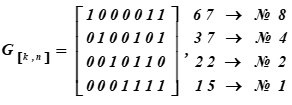
Di sebelah kanan adalah representasi desimal dari kata-kata kode Basis dari subruang dan nomor serinya di tabel K
No. i baris dari matriks adalah kata-kata dari kode yang menjadi dasar dari subruang vektor.
Contoh pengkodean kata-kata pesan informasi (matriks pembangkitan kode dibangun dari vektor basis dan sesuai dengan bagian dari tabel K). Di tabel kode ASCII, kami mengambil huruf q = <1111 0110>.
Kata-kata informasi dari pesan tersebut terlihat seperti:
...
Ini adalah setengah dari karakter (c). Untuk (7, 4) -code yang ditentukan sebelumnya, diperlukan kata-kata kode yang sesuai dengan informasi message-word (c) sebanyak 8 karakter dalam bentuk:
...
Untuk mengubah pesan-huruf ini (q) menjadi kata sandi u, setiap setengah dari pesan-huruf i dikalikan dengan matriks pembangkit G [k, n] dari kode (matriks untuk tabel K):
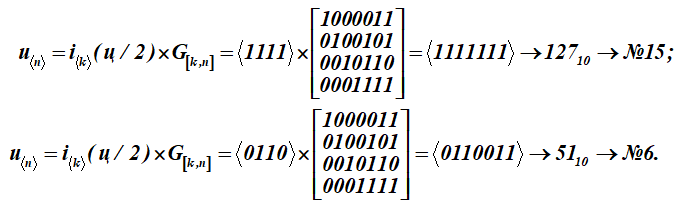
Kami mendapat dua kata sandi dengan nomor urut 15 dan 6.
Tampilkan formasi rinci dari hasil yang lebih rendah No. 6 - kata kode (perkalian baris kata informasi dengan kolom matriks pembangkit); penjumlahan atas (mod2)
<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);
<0110> ∙ <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (mod2);
<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).
Diterima sebagai hasil perkalian kata kelima belas dan keenam dari Tabel K. Empat bit pertama dalam kata kode ini (hasil perkalian) mewakili kata informasi. Mereka terlihat seperti:, (dalam tabel ASCII hanya setengah dari huruf t). Untuk matriks pengkodean, kumpulan kata-kata dengan angka: 1, 2, 4, 8 dipilih sebagai vektor basis pada tabel K. Pada tabel tersebut disorot dengan mengisi. Kemudian untuk tabel K ini matriks koding akan menerima bentuk G [k, n].
Hasil perkalian diperoleh 15 dan 6 kata dari tabel kode K.
Aplikasi kode. Dekoder
Dekoder terletak di sisi penerima saluran tempat penerima pesan berada. Tujuan decoder adalah untuk memberi penerima pesan yang ditransmisikan dalam bentuk yang ada di pengirim pada saat pengiriman, yaitu. penerima dapat menggunakan teks dan menggunakan informasi darinya untuk pekerjaan mereka selanjutnya.
Tugas utama decoder adalah untuk memeriksa apakah kata yang diterima (7 bit) adalah kata yang dikirim di sisi transmisi, apakah kata tersebut mengandung kesalahan. Untuk mengatasi masalah ini, untuk setiap kata yang diterima oleh decoder, dengan mengalikannya dengan matriks cek H [nk, n], sindrom vektor pendek S (3 bit) dihitung.
Untuk kata-kata yang merupakan kode, yaitu tidak mengandung kesalahan, sindrom selalu mengambil nilai nol S = <000>. Untuk kata dengan kesalahan, sindromnya bukan nol S ≠ 0. Nilai sindrom memungkinkan untuk mendeteksi dan melokalisasi posisi kesalahan hingga sedikit pada kata yang diterima di sisi penerima, dan dekoder dapat mengubah nilai bit ini. Dalam matriks periksa kode, dekoder menemukan kolom yang sesuai dengan nilai sindrom, dan nomor urut kolom ini sama dengan bit yang rusak karena kesalahan. Setelah itu, untuk kode biner, decoder mengubah bit ini - ganti saja dengan nilai yang berlawanan, yaitu satu diganti dengan nol, dan nol diganti dengan satu.
Kode yang dimaksud sistematis, yaitu, simbol kata informasi ditempatkan dalam satu baris di bagian paling penting dari kata kode. Pemulihan kata-kata informasi dilakukan dengan membuang bit yang paling tidak signifikan (check), yang jumlahnya diketahui. Selanjutnya, tabel kode ASCII digunakan dalam urutan terbalik: inputnya adalah urutan biner informasional, dan outputnya adalah huruf-huruf alfabet dari bahasa asli. Jadi, kode (7, 4) sistematis, grup, linier, blok, biner .
Dasar dari decoder dibentuk oleh matriks cek H [nk, n], yang berisi jumlah baris yang sama dengan jumlah simbol centang, dan semua kolom yang memungkinkan, kecuali nol, kolom tiga karakter... Matriks pemeriksa paritas dibangun dari kata-kata pada tabel K, mereka dipilih agar ortogonal dengan matriks pengkodean, yaitu. produk mereka adalah matriks nol. Matriks cek mengambil bentuk berikut dalam operasi perkalian, itu dialihkan. Untuk contoh spesifik, matriks centang H [nk, n] diberikan di bawah ini:
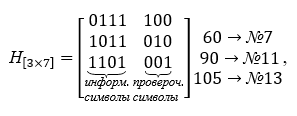



Kita melihat bahwa hasil perkalian matriks pembangkitan dan matriks cek menghasilkan matriks nol.
Contoh 2. Mendekodekan kata dari kode Hamming tanpa kesalahan (e <7> = <0000000>).
Biarkan di ujung penerima saluran menerima kata-kata # 7 → 60 dan # 13 → 105 dari tabel K,
u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0>,
dimana tidak ada kesalahan, yaitu memiliki bentuk e <7> = <0 0 0 0 0 0 0>.

Akibatnya, sindrom yang dihitung memiliki nilai nol, yang menegaskan tidak adanya kesalahan dalam kata-kata kode.
Contoh 3 . Deteksi satu kesalahan dalam satu kata yang diterima di ujung penerima saluran (Tabel K).
A) Biarkan diperlukan untuk mengirimkan codeword ke-7, mis.
u <7> = <0 1 1 1 1 0 0> dan dalam satu bit ketiga dari kiri, terjadi kesalahan. Kemudian dijumlahkan mod2 dengan kode kata ke 7 yang dikirimkan melalui saluran komunikasi
u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
dimana errornya berbentuk e <7> = <0 0 1 0 0 0 0>.
Menetapkan fakta distorsi kata kode dilakukan dengan mengalikan kata terdistorsi yang diterima dengan matriks cek kode. Hasil perkalian ini akan menjadi vektordisebut sindrom codeword.
Mari kita lakukan perkalian seperti itu untuk data asli kita (vektor ke-7 dengan kesalahan).

Sebagai hasil dari perkalian tersebut, pada ujung penerima saluran, diperoleh sindrom vektor S <nk>, yang dimensinya adalah (n - k). Jika sindrom S <3> = <0,0,0> bernilai nol, maka disimpulkan bahwa kata yang diterima di pihak penerima termasuk dalam kode C dan ditransmisikan tanpa distorsi. Jika sindrom tidak sama dengan nol S <3> ≠ <0,0,0>, maka nilainya menunjukkan adanya kesalahan dan tempatnya dalam kata. Bit terdistorsi sesuai dengan jumlah posisi kolom dari matriks [nk, n], yang bertepatan dengan sindrom tersebut. Setelah itu, bit yang terdistorsi dikoreksi, dan kata yang diterima diproses lebih lanjut oleh decoder. Dalam praktiknya, sindrom segera dihitung untuk setiap kata yang diterima, dan jika ada kesalahan, itu secara otomatis dihilangkan.
Jadi, selama kalkulasi, sindrom S = <110> sama untuk kedua kata. Kami melihat matriks cek dan menemukan kolom yang cocok dengan sindrom tersebut. Ini adalah kolom ketiga dari kiri. Oleh karena itu, kesalahan dibuat pada digit ketiga dari kiri, yang sesuai dengan kondisi contoh. Bit ketiga ini diubah ke nilai yang berlawanan dan kami mengembalikan kata-kata yang diterima oleh decoder ke bentuk kode. Kesalahan ditemukan dan diperbaiki.
Itu saja, begitulah cara kode Hamming klasik (7, 4) bekerja dan bekerja.
Banyak modifikasi dan peningkatan kode ini tidak dipertimbangkan di sini, karena bukan itu yang penting, tetapi ide-ide dan implementasinya yang secara radikal mengubah teori pengkodean, dan sebagai hasilnya, sistem komunikasi, pertukaran informasi, sistem kontrol otomatis.
Kesimpulan
Makalah ini mempertimbangkan ketentuan utama dan tugas keamanan informasi, nama teori yang dirancang untuk memecahkan masalah ini.
Tugas melindungi interaksi informasi subjek dan objek dari kesalahan lingkungan dan dari tindakan penyusup termasuk dalam kodologi.
Dipertimbangkan secara rinci adalah (7, 4) kode Hamming, yang menandai awal dari arah baru dalam teori pengkodean - sintesis kode-kode koreksi.
Penerapan metode matematika ketat yang digunakan dalam sintesis kode ditampilkan.
Contoh diberikan untuk menggambarkan efisiensi kode.
literatur
Peterson W., Weldon E. Kode koreksi kesalahan: Trans. dari bahasa Inggris. M .: Mir, 1976, 594 hal.
Bleihut R. Teori dan praktek kode kontrol kesalahan. Diterjemahkan dari bahasa Inggris. M .: Mir, 1986, 576 hal.