😘 🤷🏼 🏾 Konstruksi kurva diskon. Program pendidikan untuk seorang geek, bagian 5 🐉 ⛹🏾 🙌🏽

Mari pelajari cara membuat kurva diskon. Saya akan langsung katakan: sangat penting untuk memiliki data pasar yang terkini. Jika Anda mencari swap suku bunga untuk dolar, euro, atau mata uang lain, tidak banyak informasi terbuka di Internet. Sebagian besar data tersedia melalui terminal perdagangan atau dari perusahaan khusus - penyedia data pasar. Saya menemukan data tentang kronor Denmark, Swedia, dan Norwegia, serta data untuk euro dan dolar di situs web grup perbankan Skandinavia yang besar.

Selanjutnya, kami akan mencoba membuat kurva diskon untuk krona Swedia.

Posting ini adalah versi adaptasi dari video kuliah ketiga saya " Membangun Kurva Diskon " sebagai bagian dari kursus Finmath for Fintech.

Jadi kurva diskon untuk krona adalah tarif semalam untuk setiap hari. Hal pertama yang kita ketahui adalah apa yang disebut suku bunga dasar - suku bunga deposito pendek (pinjaman). Selanjutnya, swap dikenal mulai dari satu tahun hingga tiga puluh tahun. Untuk mengilustrasikan metode tersebut, kami akan memplot kurva hingga sepuluh tahun. Nilai data pasar saat ini dapat dilihat pada gambar berikut:

Untuk mulai memplot kurva, kita perlu membuat beberapa asumsi.

Mari kita asumsikan demi kesederhanaan bahwa swap kita adalah swap mengambang yang tetap dengan periode pembayaran setiap enam bulan. Di bawah ini adalah diagram untuk satu tahun swap. Kita tahu bahwa pada awalnya tarif dasarnya adalah nol persen. Untuk menghitung harga swap wajar, kita perlu mengetahui nilai faktor diskon enam bulan dan faktor diskon 12 bulan. Apa yang akan kita miliki sebagai "kaki" yang melayang? Misalkan karena kita akan membayar nilai rata-rata semalam untuk setiap rentang. Artinya, nilai floating "leg" hingga enam bulan - ini akan menjadi nilai rata-rata dalam semalam selama 180 hari. Kaki apung untuk poin 12 bulan akan sama, hanya saja disini akan ada penjumlahan dari hari ke 181 sampai hari ke 360.

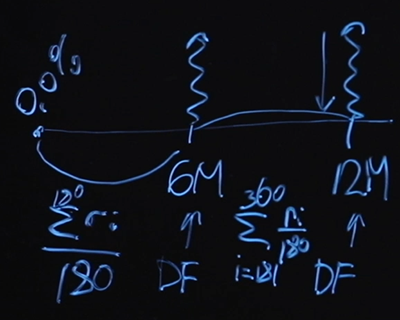
Metode rata-rata ini sudah dikenal luas. Ini disebut pertukaran indeks semalam dan sangat sering digunakan dalam produk pasar. Kaki mengambang di sini didefinisikan sebagai rata-rata selama periode tersebut.

Kami tahu tarif dasar dan biaya swap. Jelas, jika kita menulis rumus untuk harga yang wajar "langsung", maka kita akan mendapatkan terlalu banyak hal yang tidak diketahui. Kita tidak mengetahui faktor diskonto selama 6 bulan, faktor diskonto selama 12 bulan, dan kita tidak mengetahui nilai suku bunga kecuali satu - satunya yang pertama. Terlalu banyak yang tidak diketahui dan hanya satu persamaan.

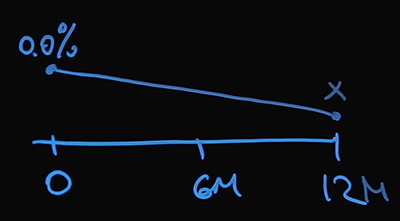
Hipotesis berikut akan membantu kami dalam memecahkan masalah ini. Kita tahu tingkat bunga di titik nol - ini adalah suku bunga dasar. Kami akan berasumsi bahwa suku bunga kami berubah secara linier. Mari kita tentukan sebagai X nilai suku bunga pada titik 12 bulan.

Pada 6 bulan itu akan menjadi X / 2 (rata-rata aritmatika antara nol dan X), dan kita dapat menemukan nilai suku bunga pada hari yang sewenang-wenang. Dan tidak ada yang sulit dalam menghitung suku bunga mengambang kami pada poin 6 dan 12 bulan:

\begin{array}{rcl} L_{1} & = & \frac{X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{X}{4} \end{eqnarray}$

\begin{array}{rcl} L_{1} & = & \frac{3 X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{3X}{4} \end{eqnarray}$

Sekarang mari beralih ke faktor diskon. Kami menggunakan kurva diskon berdasarkan tarif semalam. Oleh karena itu, faktor diskon pada titik enam bulan adalah hasil perkalian dari 180 faktor diskon pada setiap titik, dan ini jelas merupakan semacam fungsi dari X.

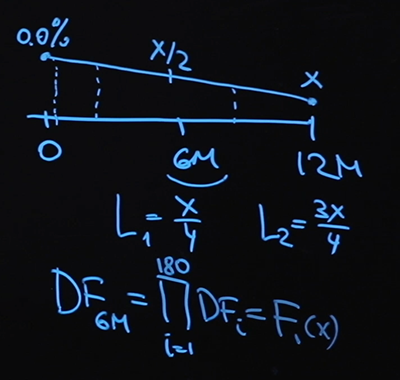
Faktor diskon pada titik 12 bulan dibangun dengan cara yang sama dengan satu-satunya perbedaan yang saya butuhkan lebih banyak pengganda. Ini juga akan menjadi beberapa fungsi X.

Jadi, faktor diskonto dinyatakan dalam X, ada juga nilai pertama dan kedua dari kurs mengambang. Mari kita lanjutkan ke penulisan persamaan. Kita tahu nilai harga swap, misalkan sama dengan P. Ingat persamaan untuk harga wajar. Kita perlu mengalikan P dengan faktor diskon pada titik dua belas bulan dan menyamakannya dengan jumlah berikut:

Saya ingatkan Anda bahwa faktor diskon untuk satu hari akan ditentukan dengan rumus berikut:

\begin{array}{rcl} D F_{i} & = & \frac{1}{(1 + \frac{r_{i}}{360})} \end{array}

$\begin{eqnarray} DF_i&=& \frac{1}{(1+\frac{r_i}{360})} \end{eqnarray}$

dimana r _i adalah nilai suku bunga. Saya menggunakan angka 360 dengan asumsi bahwa ada 360 hari dalam setahun (ini adalah ketentuan yang sangat umum untuk kalender). Pada titik tertentu, kita tahu bagaimana menyatakan faktor diskonto, r _i dinyatakan dalam X, menggunakan interpolasi linier. Persamaan kita ternyata hanya memiliki satu yang tidak diketahui, dan dapat diselesaikan dengan menggunakan metode numerik. Bagaimana melakukan ini - lihat kode Python .

Jadi, kami tahu cara menemukan nilai tarif kami pada titik 1 tahun. Dengan menggunakan asumsi interpolasi linier dan berdasarkan nilai swap yang kita ketahui dari pasar, kita akan mencari nilai X. Di sini kita menggambar bagian pertama dari kurva kita:

Nah, untuk menghitung harga swap selama dua tahun, kita membutuhkan nilai pada titik 6 bulan, 12 bulan, 18 bulan dan 2 tahun. Kami akan menggunakan asumsi yang sama persis seperti yang terakhir kali. Mari kita sebut nilai tingkat yang diinginkan Y dan juga menggunakan asumsi tentang garis interpolasi, memulihkan bagian kedua dari kurva. Jadi, selangkah demi selangkah, kita akan mencapai akhir - sampai titik 10 tahun.

Cara ini disebut bootstrap . Ini tidak sempurna atau satu-satunya yang benar, tetapi cukup sederhana untuk diterapkan dan dipahami - metode bootstrap sangat bagus sebagai level awal.

Kami menemukan kurva diskon. Apa yang diberikannya kepada kita? Secara formal, ini adalah nilai tarif semalam pada titik mana pun di masa mendatang hingga sepuluh tahun. Anda mungkin bertanya: "Siapa yang membutuhkannya?" Memang, sulit membayangkan skenario ketika klien mendatangi Anda dan berkata: "Saya ingin membuka setoran satu hari, yang akan dimulai dalam 567 hari." Ini adalah situasi yang agak tidak bisa dipahami, dan orang seharusnya tidak melihat kurva yang dibangun dalam bentuk langsung seperti itu.

Bayangkan kita memiliki semacam pembayaran di masa depan, katakanlah tujuh setengah tahun. Pertanyaan: bagaimana kita mengetahui nilainya saat ini?

Inilah pertanyaan yang akan dijawab oleh kurva diskon. Kami akan menelusuri setiap titik kurva, menghitung faktor diskon di setiap titik dan mengakhiri perjalanan kami di titik tersebut selama tujuh setengah tahun, menemukan faktor diskon yang dihasilkan, dikalikan dengan pembayaran - ini akan menjadi harga yang wajar.

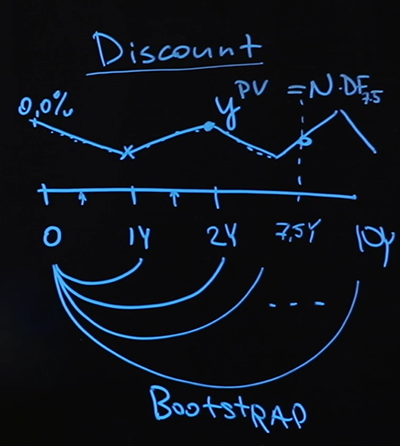
Model yang saya gunakan, yaitu floating rate yang saya ambil, cara saya menginterpolasi nilai antara, dan secara umum fakta bahwa saya memilih interpolasi sangat ditentukan oleh jenis data yang saya miliki. Saya memiliki data yang sangat sedikit - hanya satu tarif dasar dan nilai swap. Jika lebih banyak data tersedia untuk saya, atau berbeda, kemungkinan besar saya akan mengubah modelnya. Tetapi metode bootstrap (ketika Anda memplot kurva terlebih dahulu pada bagian yang pendek, lalu memplot lebih jauh dan lebih jauh, dengan mengandalkan nilai yang diperoleh sebelumnya) masih berlaku.

Sekarang ingatlah bahwa selain kurva diskon, kita membutuhkan kurva LIBOR (TIBOR, EURIBOR, dll.). Perbedaannya terletak pada alat apa yang kita tambahkan ke model kita untuk perhitungan. Kami akan mencari kontrak yang mengandung LIBOR dan dengan cara yang sama, menggunakan metode bootstrap, kami akan merekonstruksi kurva LIBOR.

Jika Anda harus membangun kurva LIBOR yang sebenarnya, berhati-hatilah dengan alat apa yang Anda gunakan untuk membuatnya, evaluasi dengan cermat model yang akan Anda gunakan. Dalam kasus ini, saya menggunakan diskon semalam, tetapi metode yang berbeda diperlukan untuk membuat kurva LIBOR. Kemungkinan besar, diskon akan dilakukan setiap tiga atau enam bulan, tergantung pada instrumennya. Jika Anda memiliki cukup data, Anda dapat memplot kurva LIBOR, kurva EURIBOR, kurva TIBOR, dan lainnya.

Jika klien mendatangi Anda dengan kata-kata: "Saya ingin swap suku bunga bukan untuk sepuluh tahun, tetapi untuk 134 bulan, di mana saya akan membayar LIBOR mengambang setiap 25 hari," ini tidak menjadi masalah. Kami memiliki kurva LIBOR, kami menggunakan asumsi interpolasi, kami dapat memulihkan nilai LIBOR di titik mana pun. Kita tahu nilai kurva diskon di setiap titik, kita juga bisa menghitung semua pembayaran dan menemukan harga "kaki" tetap yang menyeimbangkan pembayaran mengambang ini. Dengan demikian, Anda dapat menemukan nilai harga wajar untuk semua instrumen dengan memplot beberapa kurva.

Jadi, mari kita bahas sorotannya lagi. Saya mengambil data yang tersedia dan merumuskan beberapa asumsi. Pertama, jadwal pembayaran: seberapa sering, seberapa sering, masing-masing pihak membayar fixed leg dan floating leg. Kedua, bagaimana saya menghitung taruhan pada kaki mengambang? Asumsi ketiga adalah tentang interpolasi taruhan linier. Menggunakan ketiga asumsi ini, saya merumuskan beberapa persamaan nonlinier, yang saya selesaikan secara numerik. Notebook Jupyter dapat ditemukan di sini. Secara berurutan, mulai dari segmen terpendek satu tahun, lalu dua tahun, tiga, dll., Saya merekonstruksi kurva tersebut untuk selang waktu hingga 10 tahun. Ini adalah kurva diskon saya yang dapat saya gunakan untuk mengevaluasi instrumen apa pun. Metode ini disebut bootstrap: segmen kurva, yang saya hitung di awal, saya gunakan pada langkah kedua, jika tidak,apa yang saya dapatkan di langkah kedua, saya menggunakannya untuk langkah ketiga dan seterusnya, sampai kurva benar-benar terbentuk.

Saya harap sekarang Anda tidak lagi "melayang" dalam topik suku bunga mengambang dan di antara tingkat bunga swap Anda dapat menemukan vanilla. Dan Anda juga dapat membuat kurva apa pun menggunakan metode bootstrap.

Semua artikel di seri ini

Konstruksi kurva diskon. Program pendidikan untuk seorang geek, bagian 5

More articles: