- Halo semuanya, nama saya Rishat. Saya telah bekerja pada kualitas pencarian Yandex selama hampir tiga tahun. Tetapi hari ini saya ingin berbicara bukan tentang pekerjaan, tetapi tentang apa yang saya lakukan di waktu luang. Saya terlibat dalam informatika kuantum, tetapi pada kenyataannya - berbagai model perhitungan, termasuk yang kuantum.
Informatika kuantum adalah bidang yang menarik saat ini. Banyak usaha yang diinvestasikan di sana, banyak yang telah dilakukan. Dalam laporan saya, saya akan mencoba menarik minat Anda. Mungkin ada insinyur ML keren di antara Anda yang ingin melakukan pembelajaran mesin kuantum, atau hanya ahli algoritme yang kuat yang dapat mengerahkan usahanya ke arah ini. Ini akan menjadi luar biasa karena masa depan akan segera datang.
Saya harus segera mengatakan bahwa saya bukan fisikawan. Tentunya ada orang di antara Anda yang memahami semua proses ini dalam fisika lebih dari saya. Karena itu, saya hampir tidak akan mengatakan apa-apa tentang fisika.
Saya berharap dari Anda bahwa Anda sedikit ingat aljabar, ingat apa itu vektor dan bagaimana melipatgandakan vektor dengan sebuah matriks.

Bagaimana laporan saya disusun? Pertama, kita akan berbicara sedikit tentang sejarah, tentang dari mana segala sesuatu datang untuk melihat masa depan dengan penuh percaya diri. Kemudian kita akan melihat di mana ini dapat diterapkan, keadaan apa sekarang, apakah mungkin untuk melakukan sesuatu dengan tangan Anda sekarang. Kami akan menulis program Python pertama yang dapat dijalankan di komputer kuantum. Dan kemudian, sebagai bonus, saya akan menunjukkan kepada Anda beberapa contoh algoritma di mana komputasi kuantum membantu mencapai kinerja yang jauh lebih baik dibandingkan dengan yang klasik.

Bagaimana semuanya dimulai? Dari pemuda ini. Ini adalah Alan Turing, ia dapat dengan aman disebut sebagai bapak ilmu komputer atau ilmu komputer, yang dengannya kita semua hidup sekarang, menghasilkan uang. Pada 1930-an, Turing membuat model perhitungan yang sekarang kita sebut komputer yang bisa diprogram. Tetapi adakah yang akan mengenali orang ini?

Lebih sulit. Nama keluarganya sangat sering di sebelah nama keluarga Turing. Ini adalah Gereja Alonzo, ia juga berurusan dengan masalah kemampuan komputasi, dan bahkan sedikit sebelum Turing membuat model perhitungannya sendiri. Tapi karya Turing menjadi lebih populer. Dan secara umum, Gereja pada beberapa titik adalah penasihat ilmiah Turing. Secara keseluruhan, nama mereka biasanya dikaitkan dengan tesis ini.
Tesis Church-Turing mengatakan: proses apa pun dapat dimodelkan secara efisien pada mesin Turing. Ini adalah akhir 30-an - awal 40-an, dan semuanya sangat baik. Selama sekitar 30 tahun semuanya sangat baik, sampai kedua orang ini muncul. Apakah ada yang mengenal mereka?

Ini sudah tahun 70-an, sangat dekat dengan saat ini. Nama belakang mereka sering ditemukan dalam kursus kriptografi. Ini adalah Robert Nightingale dan Volker Strassen. Kedua orang ini terkenal dengan algoritma probabilistik untuk memeriksa nomor untuk kesederhanaan, tes Solovey-Strassen.
Dan ini adalah poin yang sangat penting bagi kami, karena sampai sekarang kami mengatakan bahwa setiap proses algoritmik dapat dimodelkan pada mesin Turing. Tetapi sekarang ternyata algoritma mereka tidak dapat dimodelkan. Itu probabilistik, tidak ada yang seperti itu di mesin Turing.
Saya harus membuat perbaikan cepat dan mengatakan bahwa proses apa pun dapat dimodelkan pada mesin Turing probabilistik. Ini tidak terlalu keren lagi, pasti salah satu dari Anda memiliki cubitan di dada Anda. Anda berpikir: bagaimana bisa begitu? Sekarang kita mengatakan "probabilistik", dalam sepuluh tahun sesuatu yang lain akan ditemukan, sesuatu yang lain harus diperbaiki. Ini tidak terlalu menyenangkan. Tetapi Anda dan saya, tentu saja, tidak sendirian.

Ada pemuda lain - David Deutsch. Dan dia juga bertanya-tanya: bagaimana bisa begitu? Bagaimana untuk hidup? Dia adalah seorang ahli fisika dengan pelatihan, mengabdikan seluruh hidupnya untuk fisika. Dan saya memutuskan untuk mengatasi masalah ini dari sudut pandang fisika. Dia berkata: mari kita coba untuk membuktikan, dapatkan sesuatu sehingga alam sendiri memberi tahu kita bahwa inilah yang sebenarnya terjadi. Dan alam sudah mengatakan (dan kami masih percaya) bahwa itu adalah mekanika kuantum. Jadi kami mulai mencari jawaban dalam mekanika kuantum. Dan dengan David Deutsch, dengan algoritma pertamanya, informatika kuantum dimulai.
Ini adalah perjalanan kecil ke dalam sejarah sehingga Anda mengerti: itu tidak muncul tiba-tiba. Di daerah ini ada masalah nyata, teoretis, tentu saja, yang menyiksa orang-orang yang memulai semuanya.
Tetapi apakah semuanya hanya pada level teori? Secara umum, dari sudut pandang matematika, tidak ada masalah yang tersisa. Secara matematis, kita tahu segalanya tentang bagaimana komputer kuantum seharusnya bekerja. Sekarang sudah ada komputer kuantum nyata dari berbagai konfigurasi, bekerja dengan cara yang berbeda. Dan ini, pada umumnya, merupakan tantangan teknik.
Misalnya, di lembaga kami, kami memiliki seluruh departemen yang berurusan dengan informatika kuantum. Ada ahli matematika dan fisikawan. Fisikawan sekarang sangat terlibat dalam masalah penyimpanan informasi kuantum jangka panjang. Ini sangat mirip dengan hard drive kami, tetapi kami ingin informasi kuantum disimpan di sana.

Apa kegunaan dari seluruh perekonomian ini? Tentu saja, hal pertama yang terlintas dalam pikiran adalah pemodelan proses, karena dunia adalah mekanika kuantum. Dan jika kita menggunakan komputer kuantum untuk mensimulasikan proses, reaksi kimia, atau apa pun, itu akan jauh lebih murah secara komputasi.
Bagian kedua dan sangat besar, yang mana banyak upaya sekarang dikhususkan, adalah pembelajaran mesin kuantum. Ada harapan besar bahwa komputasi kuantum akan membantu mempercepat proses pembelajaran itu sendiri dan meningkatkan algoritma. Ada banyak pekerjaan di sini. Sekarang, misalnya, grup kuantum kami bekerja bersama dengan seorang ilmuwan dari Tiongkok. Dia adalah insinyur ML yang sangat kuat, dan kami memiliki sedikit bias kuantum, mencoba untuk membuat sesuatu bersama.
Hal ketiga agak hype beberapa bulan yang lalu. Sekarang, mungkin hype sudah tidur, tetapi bahkan ada blockchain kuantum keseluruhan. Itu ditemukan oleh teman baik saya dan teman baik. Ini aku, kataku sedikit dengan bangga.
Tetapi kami tidak memiliki komputer kuantum. Sayangnya, kami tidak dapat pulang dan menjalankan program semudah kami memprogram dengan Python.
Apa yang harus dilakukan? Saya sedang memikirkan apa yang harus saya lakukan di tahun ketiga ketika saya sedang menulis makalah semester pertama saya. Saya sedang menulis emulator komputasi kuantum. Tentu saja, semua orang menulis emulator dan semua orang menggunakannya entah bagaimana. Di tahun keempat saya, saya menulis sebuah emulator yang mensimulasikan gangguan, kebisingan, dan sebagainya. Dan kemudian aku bosan.
Saya mencoba mencari di mesin pencari dan menyadari bahwa ada banyak emulator. Berikut ini beberapa tautan, mereka cukup sederhana dan menarik:
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
Tapi saya ingin berhenti di qiskit. Dia spesial, menonjol dari semua. Dari?
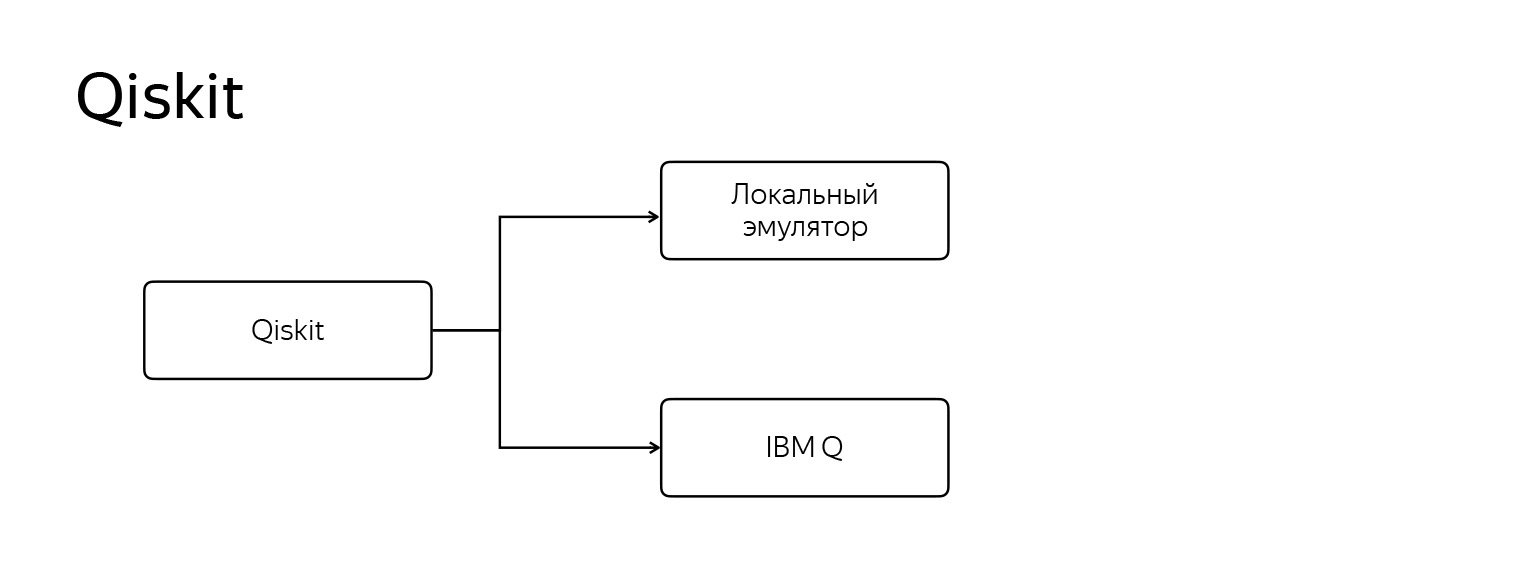
Ini bekerja dalam dua mode. Yang pertama adalah, seperti orang lain, emulator lokal biasa. Yang kedua adalah menjalankan program Anda pada komputer kuantum Q IBM nyata, yang terlihat seperti ini.

Sekarang ini adalah seluruh barel di mana suhu yang sangat rendah dipertahankan - sekitar tiga millikelvin. Ini sangat dingin. Dan IBM menyediakan kemampuan berbasis cloud untuk menghubungkan dan menjalankan kode Anda langsung di mesin itu.
Tentu saja, dia mengkompilasi perintah dan sebagainya dengan cara khusus. Bagaimana cara kerjanya? Ada beberapa instalasi komputer semacam itu untuk akses umum. Salah satunya adalah 5-qubit, ada 15-qubit, 16-qubit, bahkan 20 qubit tersedia untuk kita. Ini adalah sekitar 20 bit informasi biasa, klasik, tetapi sudah sesuatu.
Di sini, pasti, banyak dari Anda berpikir: itu dia, saya menginginkannya! Tapi kamu harus ingat sedikit matematika. Sedikit aljabar, tapi hanya sedikit, seperti yang aku janjikan.
Untuk memulai pemrograman pada komputer kuantum, Anda perlu memahami apa itu qubit. Itu hanya vektor dalam ruang vektor 2-D. Tetapi karena kita berbicara tentang ruang vektor, mereka memiliki dasar.

Dasarnya terlihat seperti ini. Ada dua kolom vektor dan satuan dasar, standar, dalam kursus aljabar yang dilambangkan sebagai berikut:
dan
. Dan ada notasi standar dalam notasi Dirac, dalam kurung sudut ini.
Maksudnya, agar Anda tidak bingung, saya akan terus mempersingkat seperti ini.
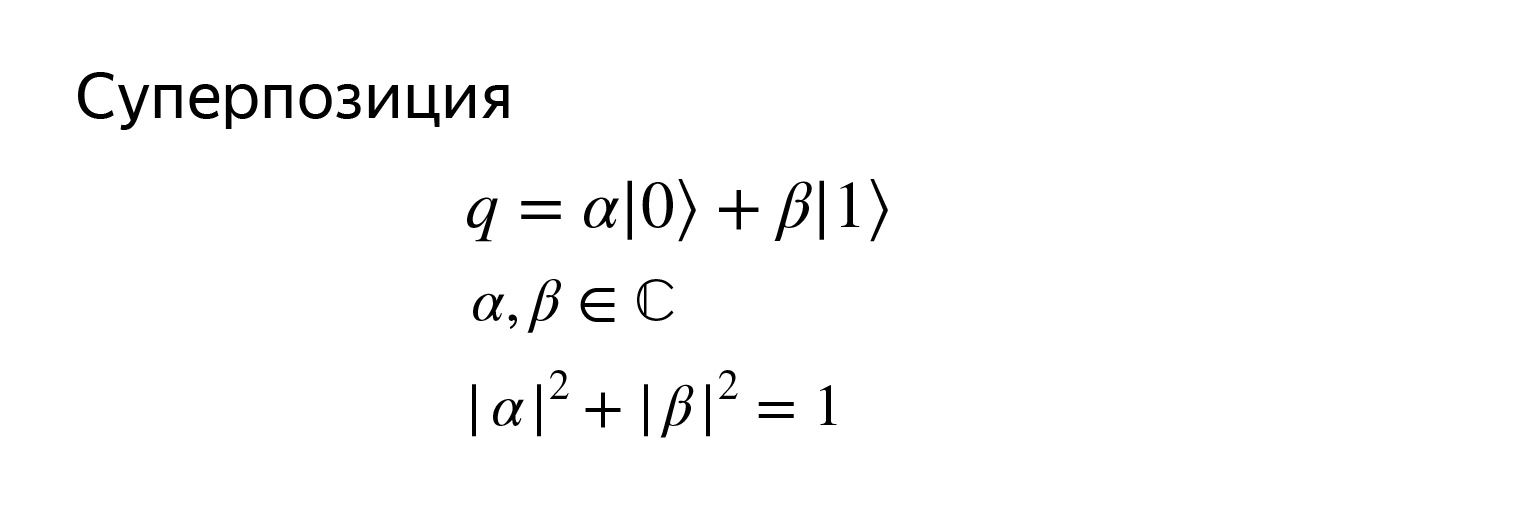
Dan karena itu adalah vektor, kondisinya dapat ditulis seperti ini. Qubit q adalah superposisi dari dua vektor basis, di mana α dan β adalah bilangan kompleks, tetapi tidak mutlak bilangan apa pun, tetapi sehingga jumlah moduli kuadratnya sama dengan satu.
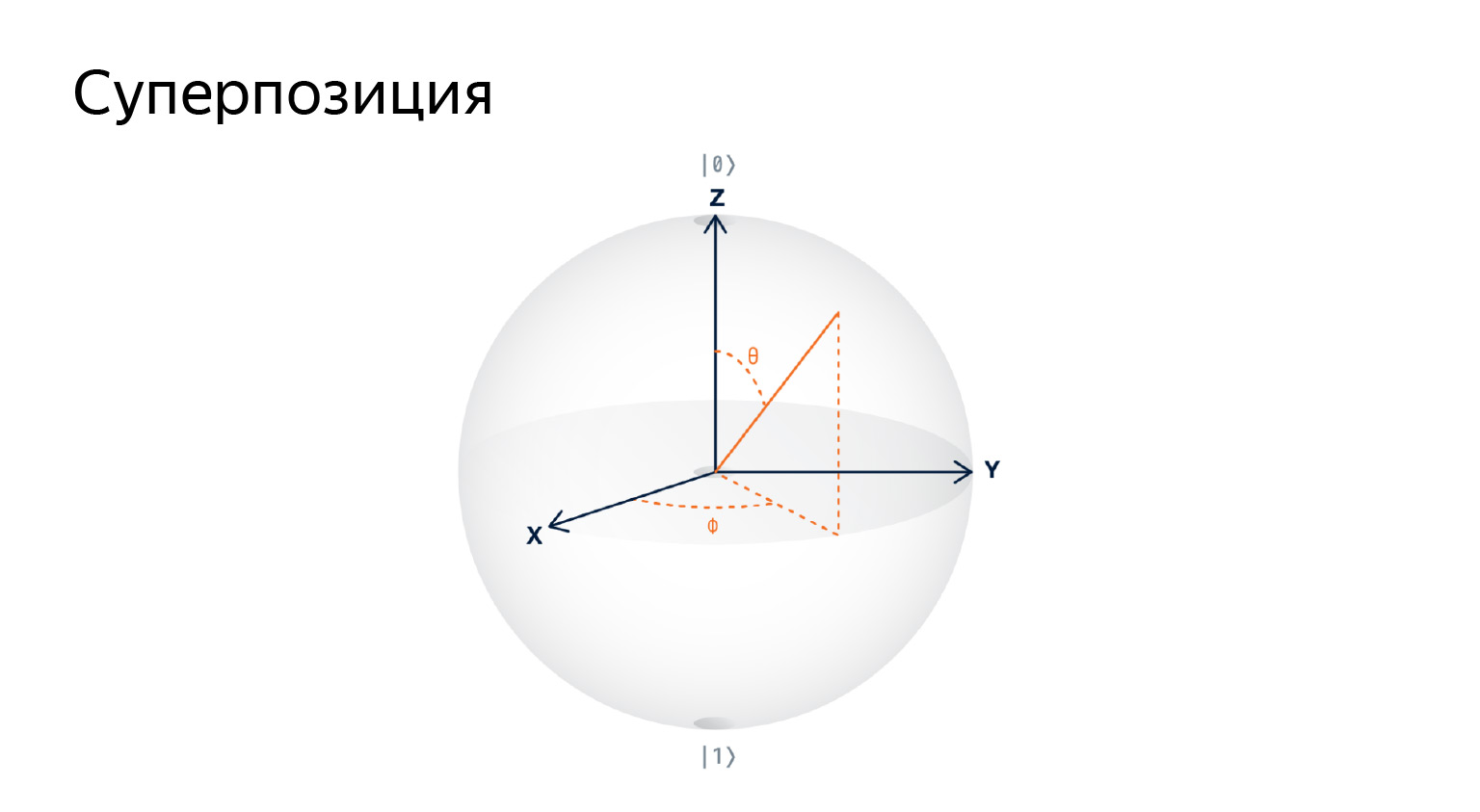
Jika kita mencoba menggambar benda ini, kita mendapatkan bahwa qubit adalah vektor pada bola tiga dimensi. Jumlah informasi yang tak terbatas dapat disimpan dalam satu qubit, karena itu hanya sebuah vektor, di mana ada jumlah yang tak terbatas.
Anda tidak perlu memperhatikan gambar, itu hanya teknik visualisasi untuk menarik perhatian.
Kami berbicara tentang qubit. Yang terpenting, qubit adalah vektor. Vektor dalam ruang vektor yang kompleks. Apa yang bisa kamu lakukan dengan itu?
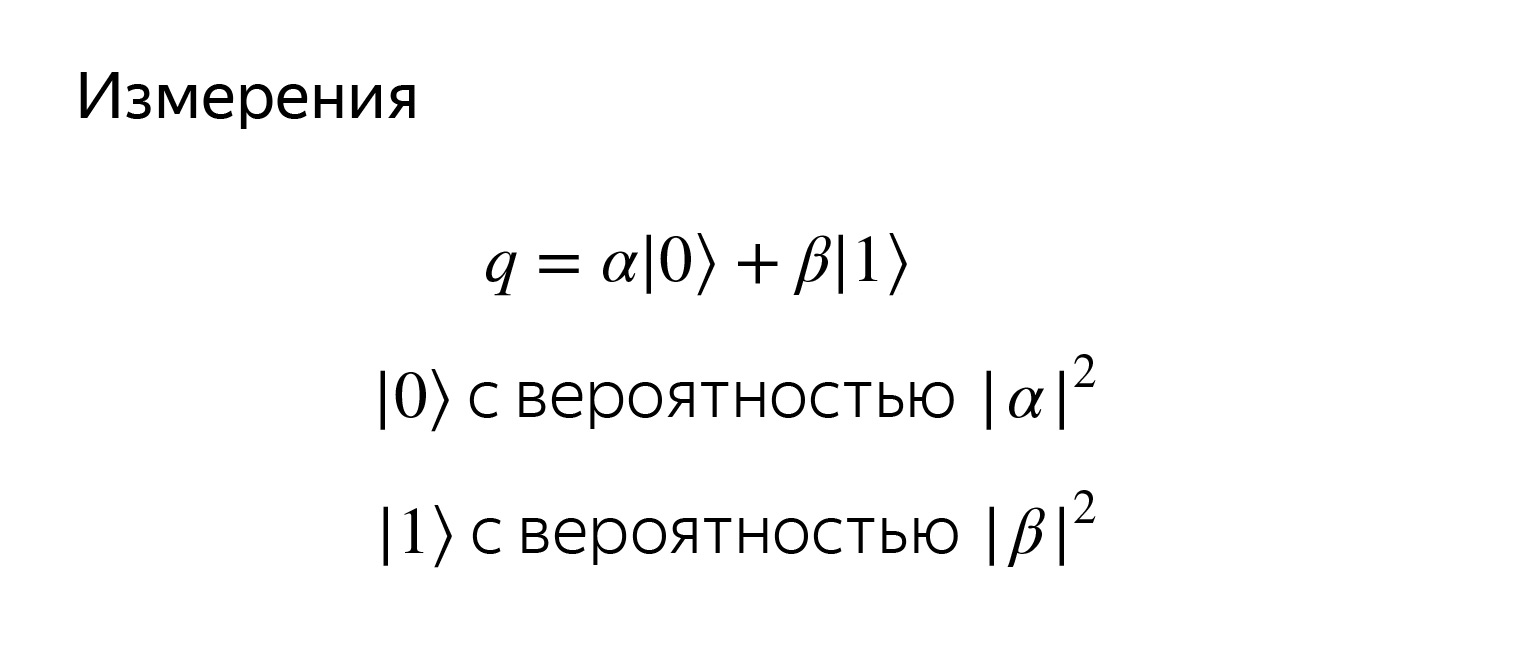
Hal pertama yang biasa kita lakukan adalah mencoba menghitung nilai variabel kita, misalnya dengan Python. Kami ingin membaca status qubit. Tapi kita tidak akan pernah tahu arti sebenarnya dari α dan β.
Jika kita mencoba melihat qubit, membacanya, maka kita mendapatkan nol atau satu dengan probabilitas yang sesuai. Probabilitas hanyalah proyeksi ke vektor basis yang sesuai.
Hal kedua yang bisa kita lakukan adalah, misalnya, mengkloning qubit. Kami menyebut ini menugaskan satu variabel ke variabel lain. Sayangnya, ini tidak dapat dilakukan di dunia kuantum.

Tidak ada operasi penugasan, dan ini sangat terkait dengan apa yang saya katakan: kita bahkan tidak akan dapat melihat nilai yang tepat. Ini adalah hasil mendasar. Terbukti sangat sederhana : secara harfiah dua garis perbandingan, dengan kontradiksi.
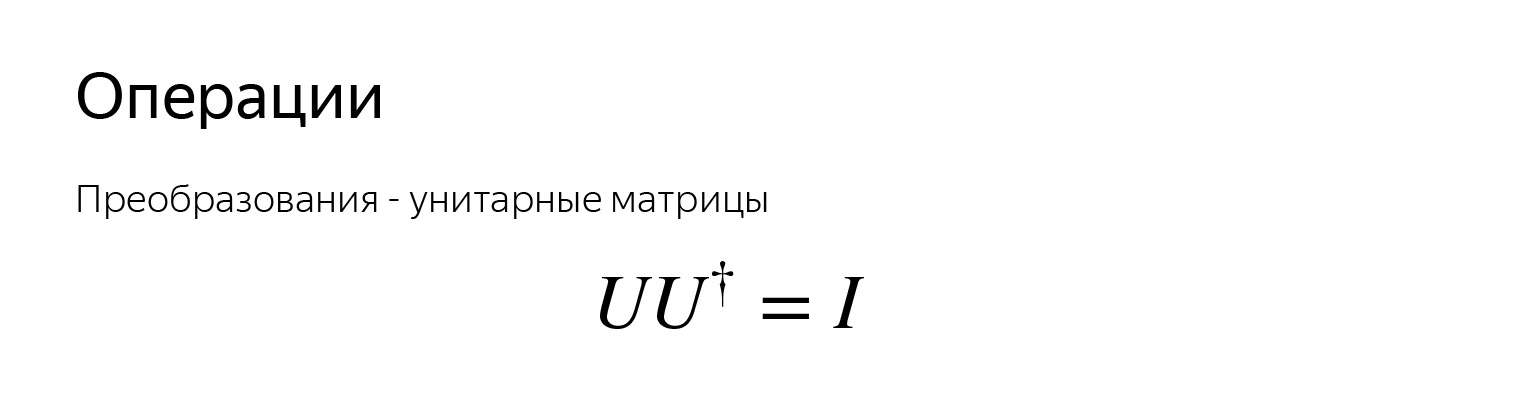
Ada qubit yang tidak bisa kita baca, kita tidak bisa mengkloning. Apa yang bisa kamu lakukan?
Qubit adalah vektor. Vektor dapat diambil dan diputar di sekitar bola. Untuk memutar, Anda dapat memikirkan matriks yang membuat rotasi ini. Semua operasi pada qubit adalah matriks. Mereka disebut kesatuan.
Kesatuan - untuk kondisi yang harus dipenuhi, itu ditulis di sini dengan cara yang licik. Ikon ini menunjukkan matriks konjugat transposif dan kompleks. Properti ini sangat penting, artinya ada kebalikan dari operasi apa pun. Artinya, tidak masalah bagaimana kita memutar vektor, kita selalu dapat mengembalikannya ke posisi sebelumnya. Selalu ada operasi terbalik.
Mari kita lihat operasi apa yang bisa dilakukan. Apa yang kita terbiasa dalam kasus klasik. Ada nol, Anda bisa mengubahnya menjadi satu dan sebaliknya.
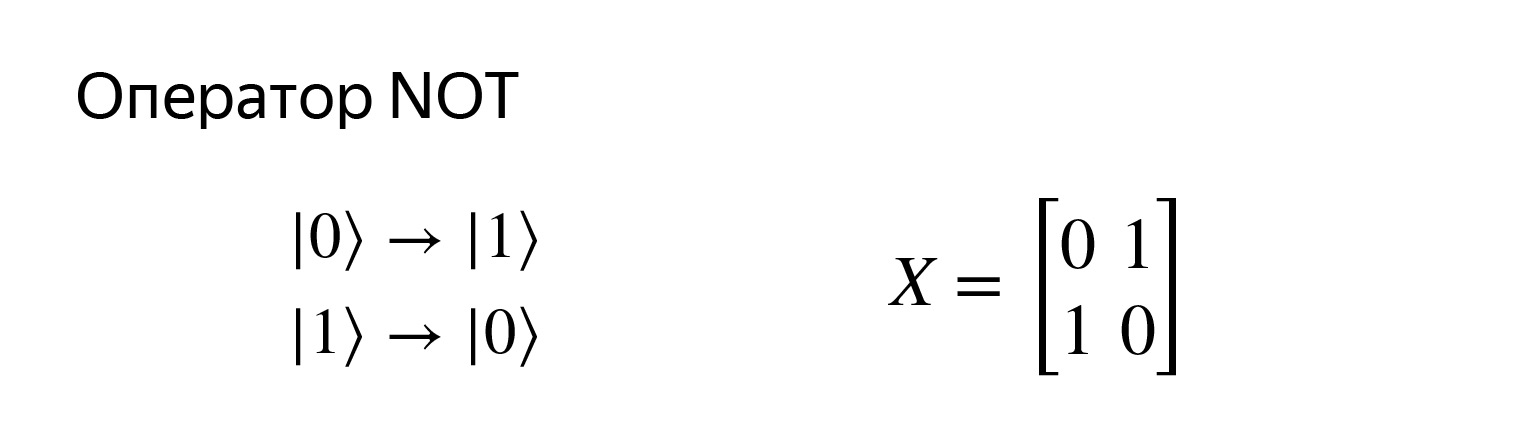
Ini adalah operator negasi dan sangat sederhana. Itu direkam dengan matriks seperti itu. Jika kita mencoba memperbanyak, kita mendapatkan apa yang kita inginkan.
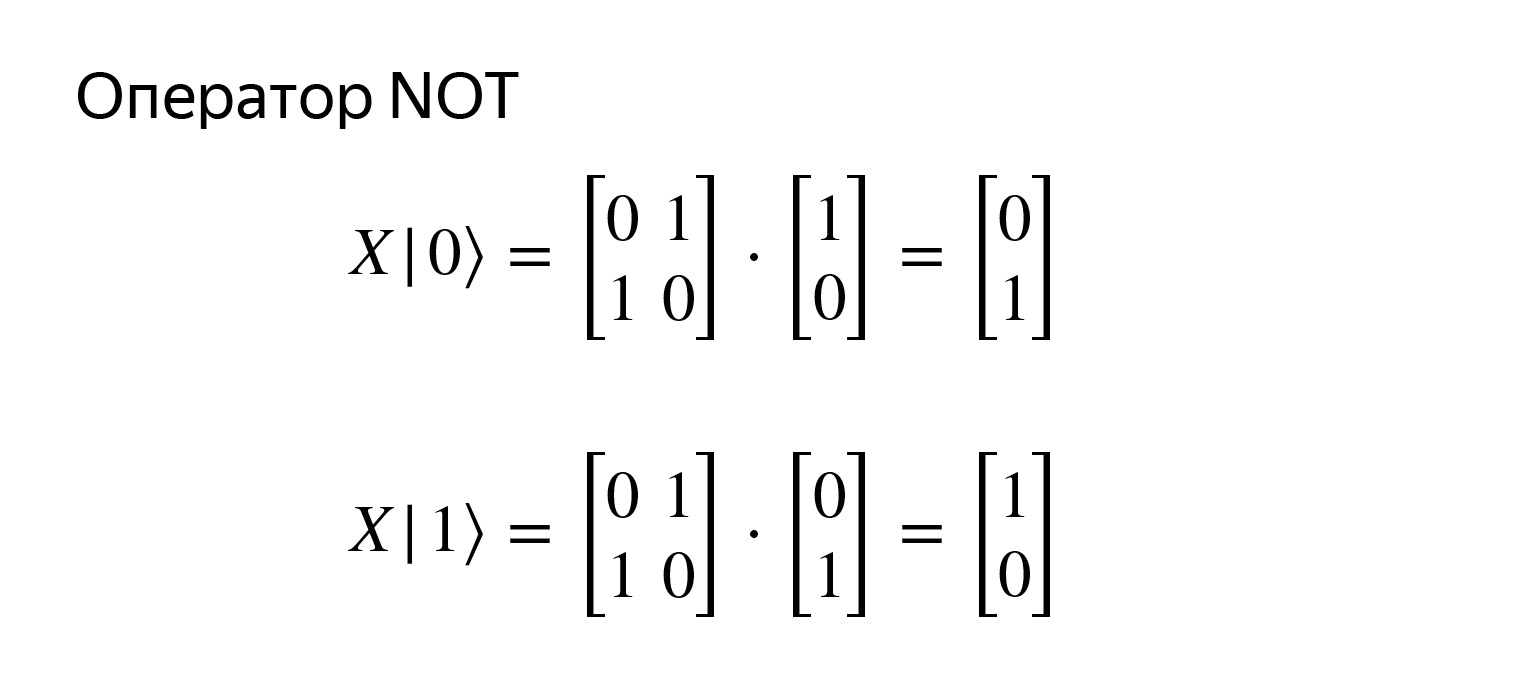
Aku bahkan sudah menggambarnya di sini. Tidak ada yang rumit. Operator negasi memiliki notasi standar, operator X. Kalau dipikir-pikir, itu hanya rotasi di sekitar salah satu sumbu. Dan ada operator Y dan Z, rotasi di sekitar sumbu lain, tapi ini tidak begitu penting sekarang.
Dan kita sudah bisa menjalankan program pertama kita di komputer kuantum yang akan meniadakan qubit.
Tapi kami dalam ilmu komputer kuantum, tentu saja, sangat jarang menulis dengan Python. Kami lebih sering menggunakan skema.

Diagram biasanya terlihat seperti ini. Garis horizontal hanyalah nilai qubit. Saya memiliki lima dari mereka tertarik di sini. Dan di blok - operasi yang akan kita lakukan.
Blok pertama. Alat pengukur diambil di sini. Ini berarti bahwa kami hanya ingin mengukur apa yang ada dalam qubit pertama.
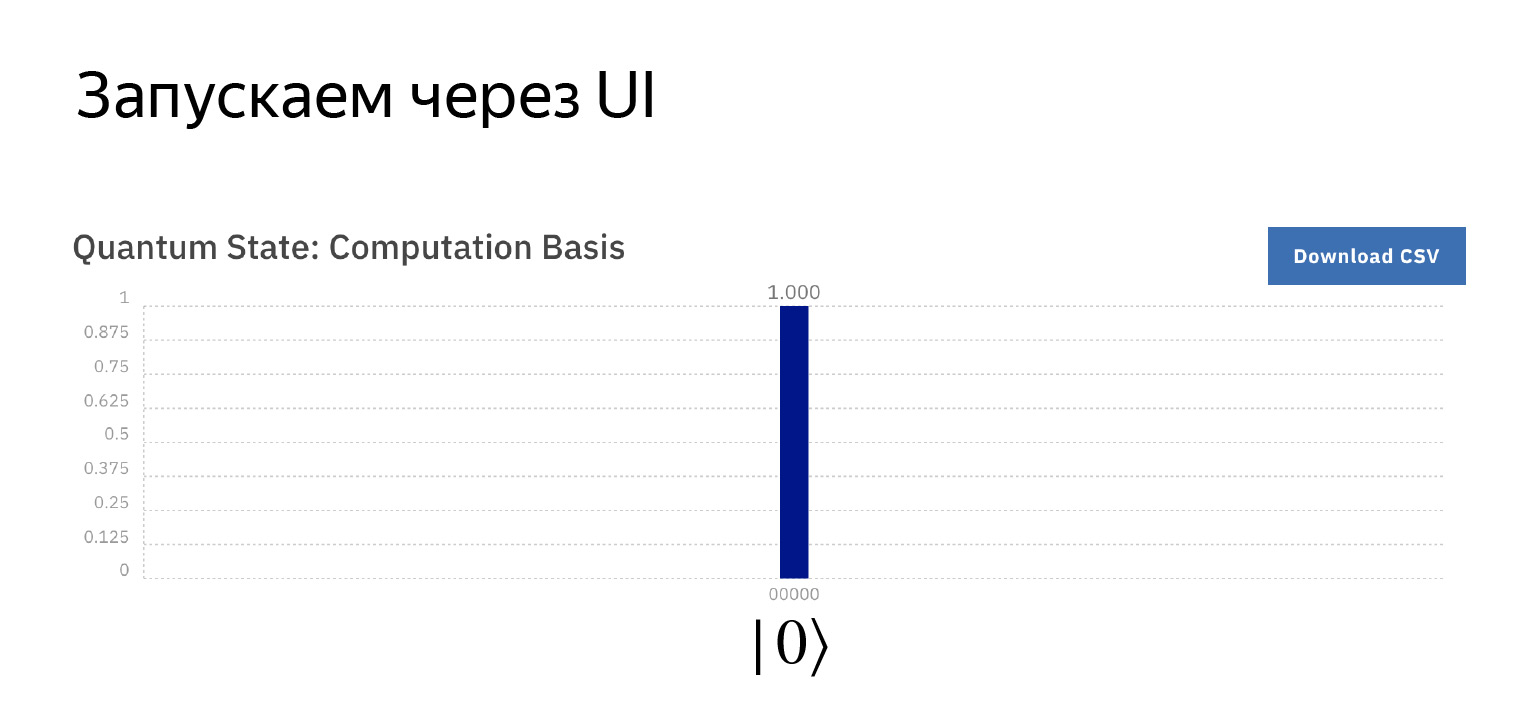
Jika kita menjalankan hal ini, kita mendapatkannya dengan probabilitas satu kita memiliki nol di sana, karena mereka diinisialisasi dalam keadaan ini dan kita tidak melakukan apa-apa dengan mereka.
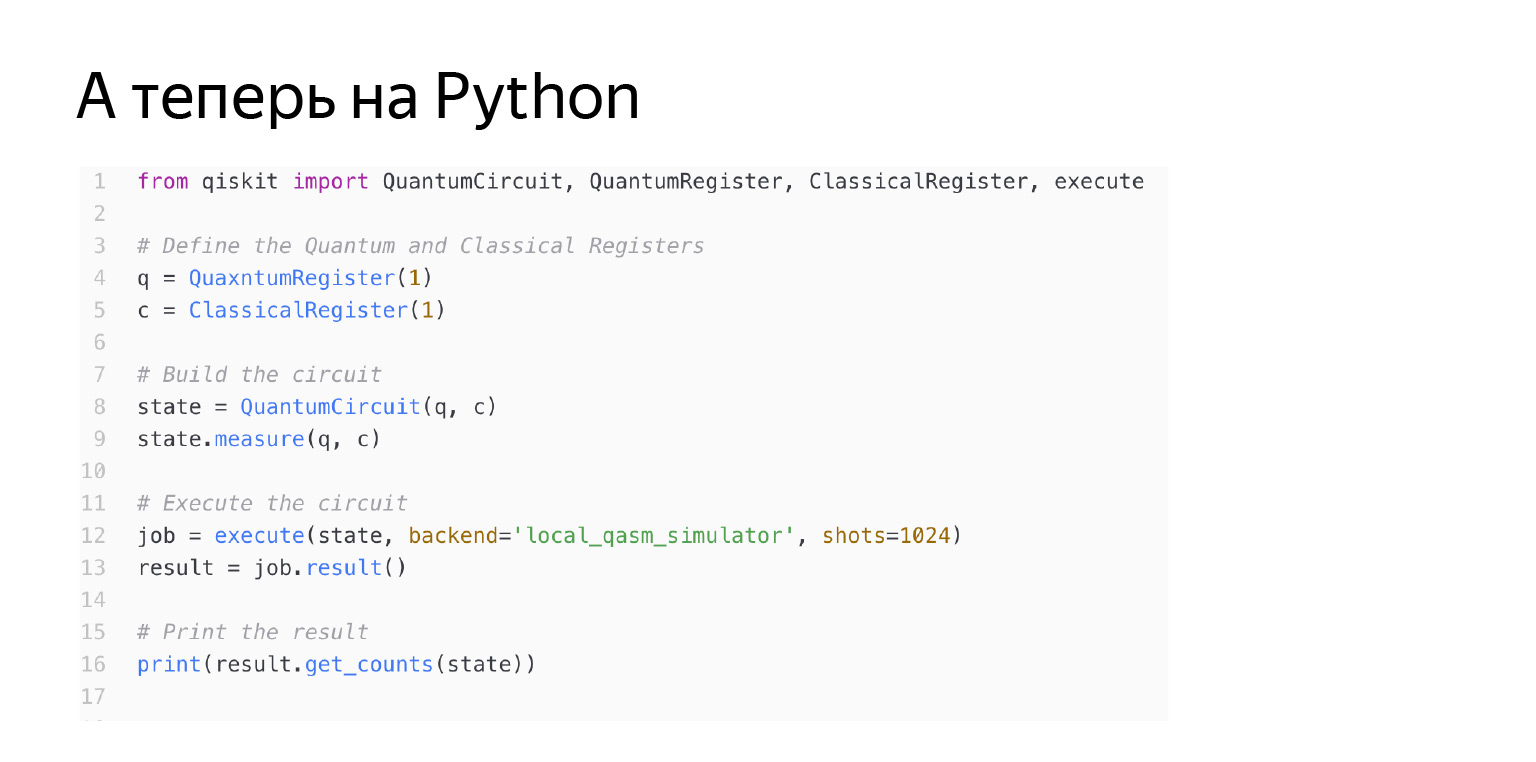
Hal seperti itu dapat ditulis dalam Python menggunakan perpustakaan qiskit. Mari kita lihat apa yang terjadi di sini baris demi baris. Pertama, kita mulai register kuantum. Saya menyalakannya di sini dari satu qubit. Dan register klasik. Register klasik diperlukan untuk menulis hasil pengukuran di suatu tempat. Yaitu, saya melakukan transformasi dengan register kuantum, hasilnya klasik satu - nol atau satu. Dan kemudian saya membuat sirkuit saya sendiri, yang memiliki qubit klasik kuantum ini. Saya hanya mengatakan: mari kita mengukur q qubit di C. Mari kita mulai semua ini dan semuanya akan baik-baik saja. Tetapi pembaca yang penuh perhatian akan melihat: dikatakan di sini bahwa backend saya adalah emulator lokal.

Hal yang sama dapat dilakukan dengan IBM Q, tetapi ada lebih banyak kode di sini. Ada banyak jenis mie tentang memilih perangkat yang akan merespons kami sesegera mungkin, mentransfer beberapa token, itu saja. Tapi tidak ada yang rumit.

Hal yang sama dapat dilakukan dengan operator negasi. Ini adalah operator X, seperti yang saya katakan. Itu terlihat persis sama pada diagram, mari kita jalankan yang sama.
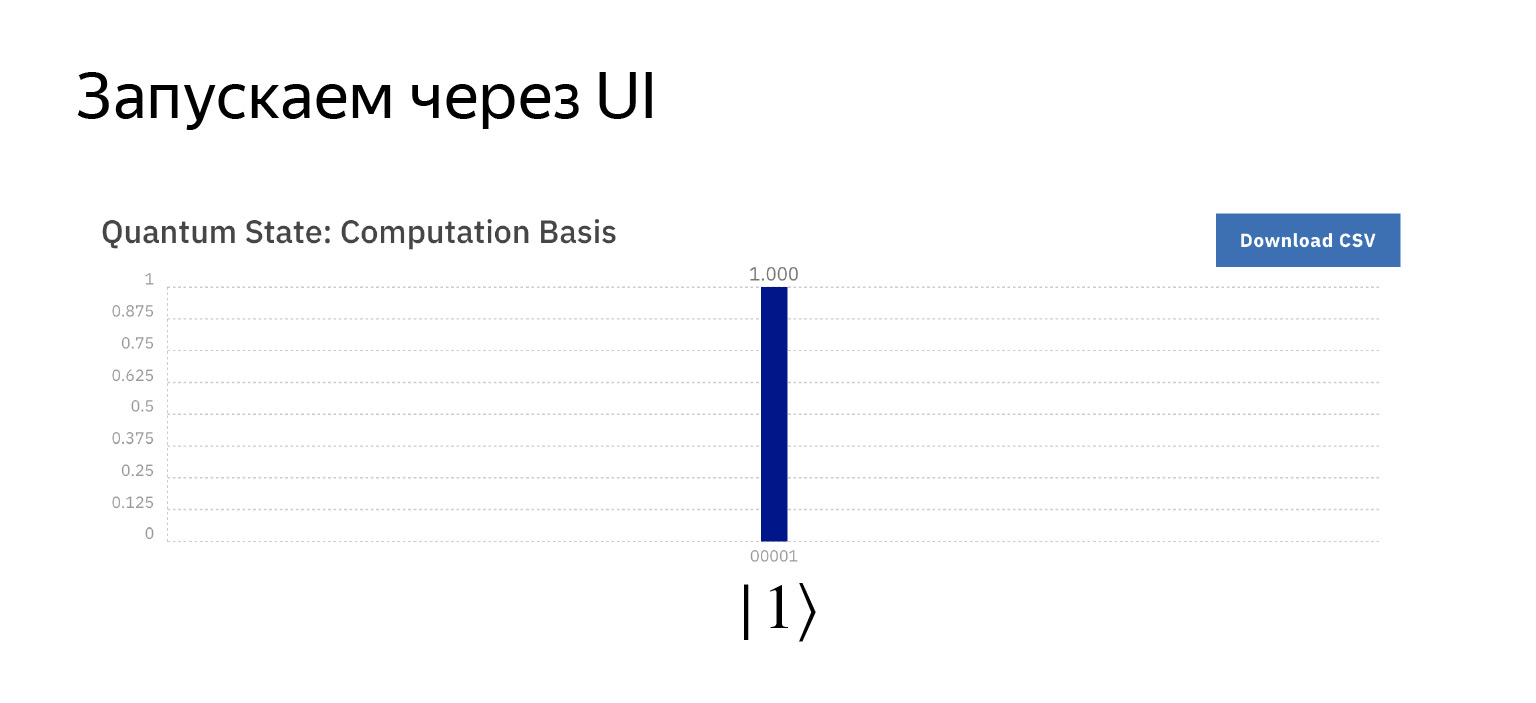
Sekarang, dengan probabilitas satu, kita mendapatkannya, sesuai rencana. Tanpa sihir.
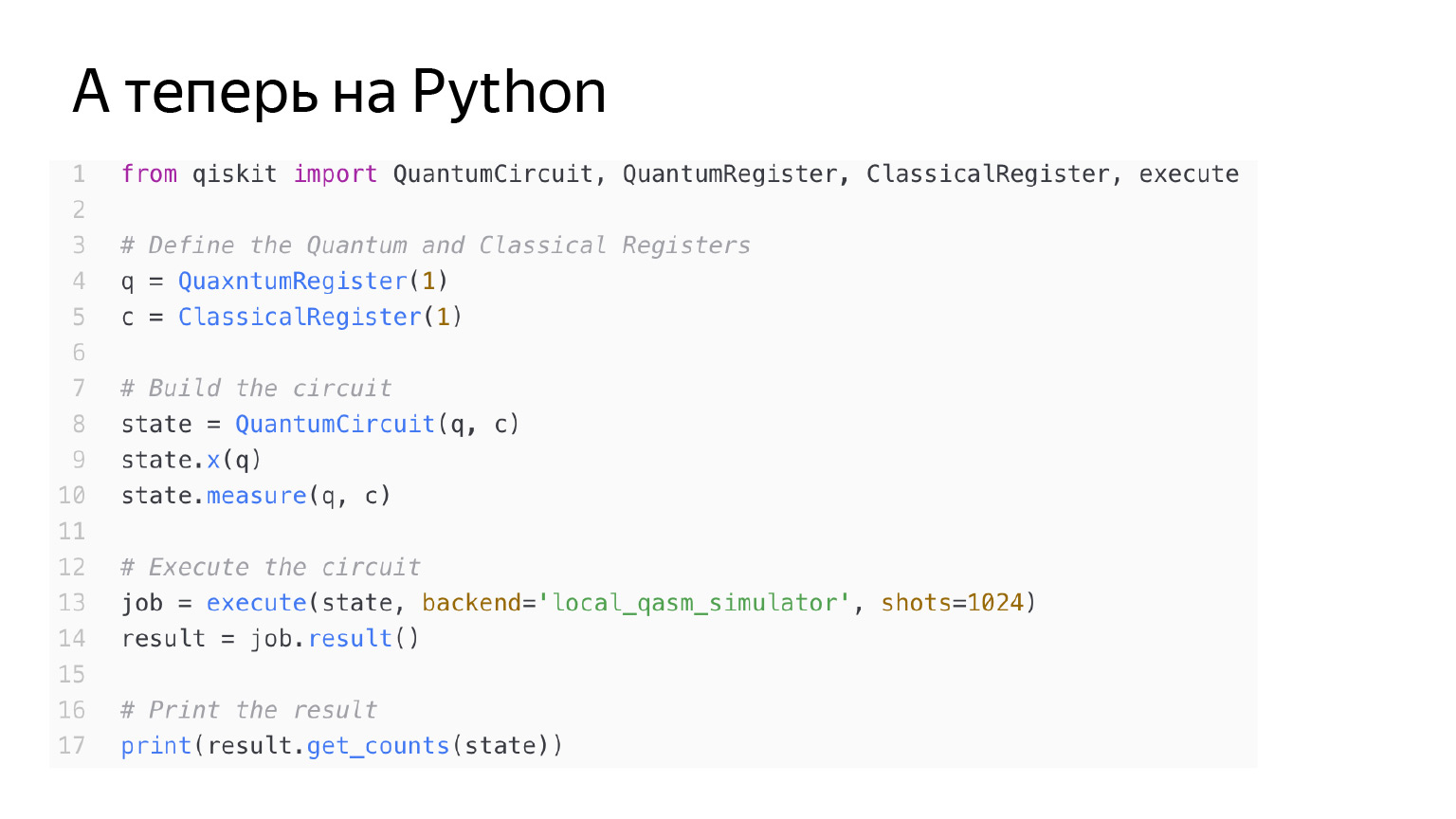
Kodenya sama. Hanya saja di sini saya juga menerapkan operator X ke q qubit.
Oke, mari kita coba melangkah lebih jauh.
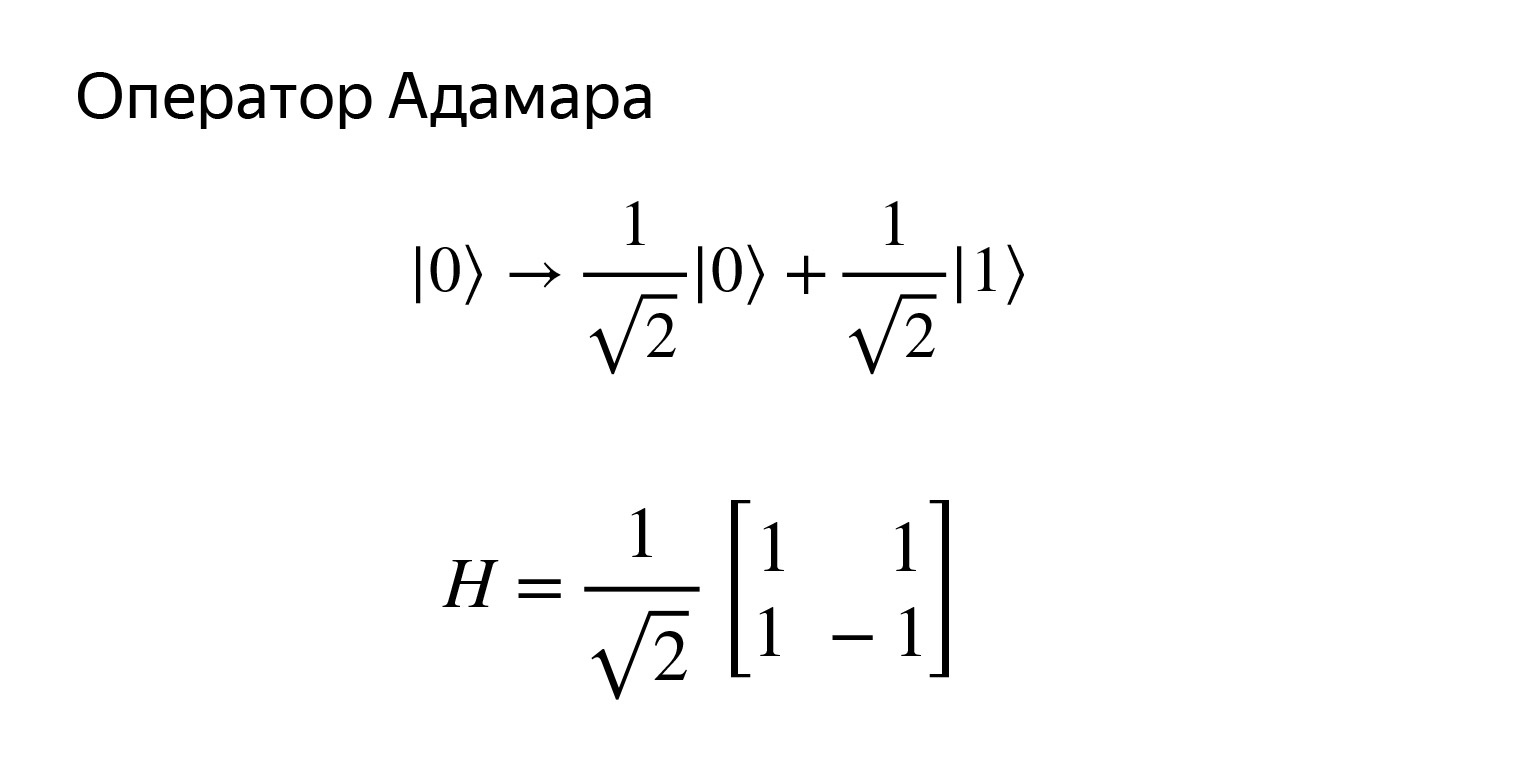
Ada hal yang sangat sulit di sini. Mari kita coba untuk mendapatkan status ini. Keadaan ini sangat menarik. Kami akan mendapatkan superposisi seperti itu. Jika kita mencoba mengukurnya, maka dengan probabilitas 1/2 kita mendapatkan nol atau satu. Artinya, itu akan menjadi superposisi yang seragam, kita bisa mendapatkan apa saja.
Sebuah analogi dapat ditarik ke apa yang disebut lemparan koin kuantum. Kita akan mengatakan oke, dengan probabilitas ½ kita mendapat nol dan satu. Matriksnya terlihat seperti ini.
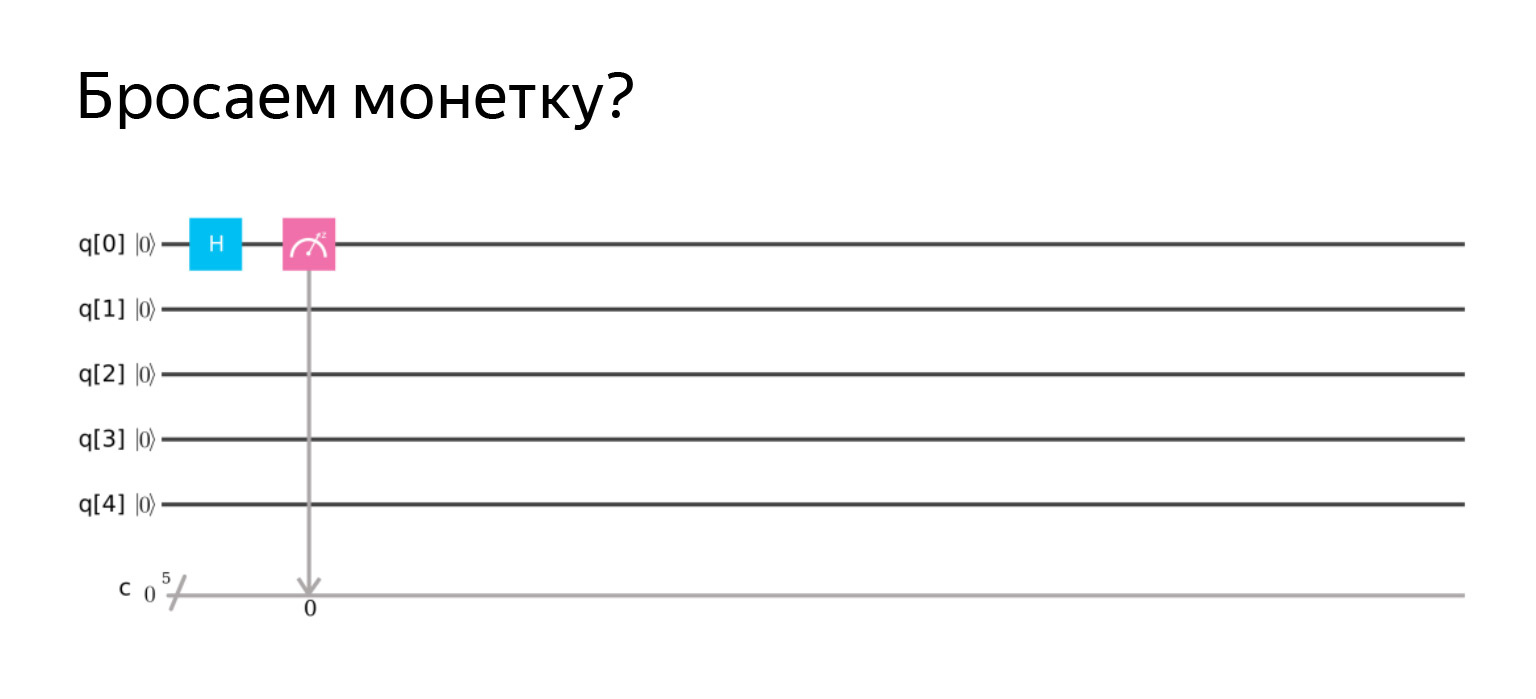
Mudah diperiksa, tetapi tentu saja tidak. Mari menggambar diagram. Operator H untuk menghormati Hadamard.
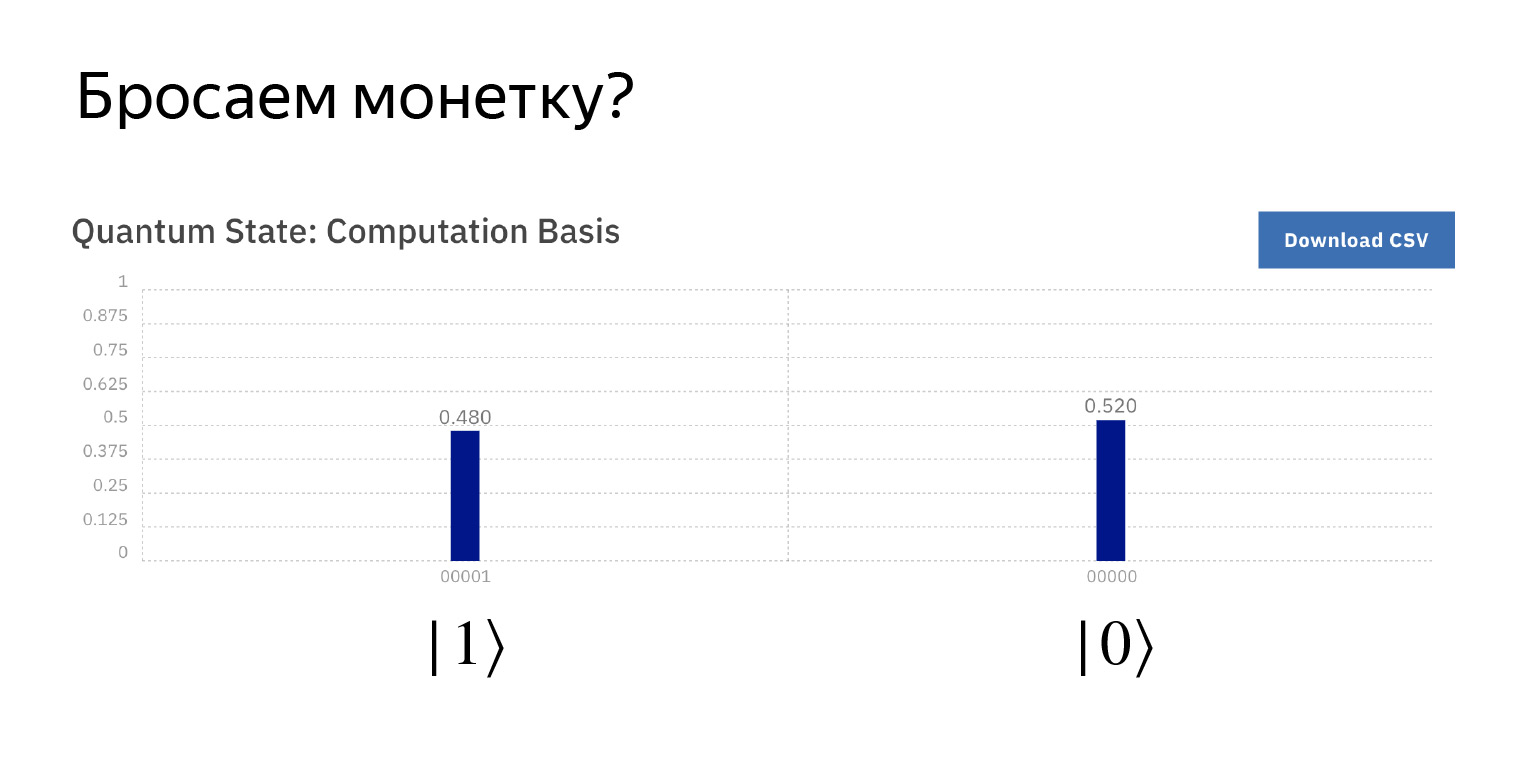
Mari kita ukur dan dapatkan kira-kira apa yang kita harapkan. Dengan probabilitas ½, nol dan satu. Sedikit lagi, sedikit lagi, tapi begitulah cara kerjanya.
Berikut kode Python, hanya untuk berada di sana, kami berada di konferensi Python.

Ada superposisi seperti itu. Kami menerapkan operator Hadamard untuk itu dan mengukur.
Tetapi Anda dapat membalik koin dua kali, kita semua terbiasa dengan ini. Jika Anda membalik koin dua kali, tidak ada yang berubah. Mari kita coba melakukan ini dalam kasus kuantum.

Kami menerapkan operator Hadamard dua kali berturut-turut dan kami selalu mendapatkan nol.

Artinya, jika Anda membalik koin kuantum dua kali, Anda akan selalu mendapatkan nol, karena operator Hadamard terbalik dengan dirinya sendiri. Jika Anda mengalikannya sendiri, Anda selalu mendapatkannya. Ada satu hal.
Jadi, Anda dapat melakukan sesuatu dengan satu qubit. Dapat diputar, diputar dan diukur. Mari coba tambahkan lebih banyak qubit. Apa yang biasa kita lakukan di dunia klasik? Ambil dan lakukan operasi logis sederhana, "atau" dan "dan".

Di dunia kuantum, Anda tidak dapat melakukan ini, karena mereka tidak sepenuhnya dapat dibalik. Artinya, mendapatkan nol dalam operasi "dan", kita tidak akan pernah tahu apa nilai awal itu.
Dan di dunia kuantum, seperti yang saya katakan, operasi adalah matriks kesatuan yang selalu dapat dibalik. Jadi, bagaimana Anda memprogram sama sekali? Segala sesuatu yang kita terbiasa hancur. Tetapi seorang pahlawan baru muncul, ini adalah operator yang disebut negasi terkontrol.

Jika kami menulis dengan Python, akan terlihat seperti ini. Jika qubit pertama adalah satu, mari balikkan qubit kedua. Ini bukan sebuah matriks, ini adalah apa yang terlihat seperti operator. Tetapi pada prinsipnya, apa yang saya katakan tertulis di sini. Di mana ada kesatuan dalam qubit pertama, yang kedua terbalik.
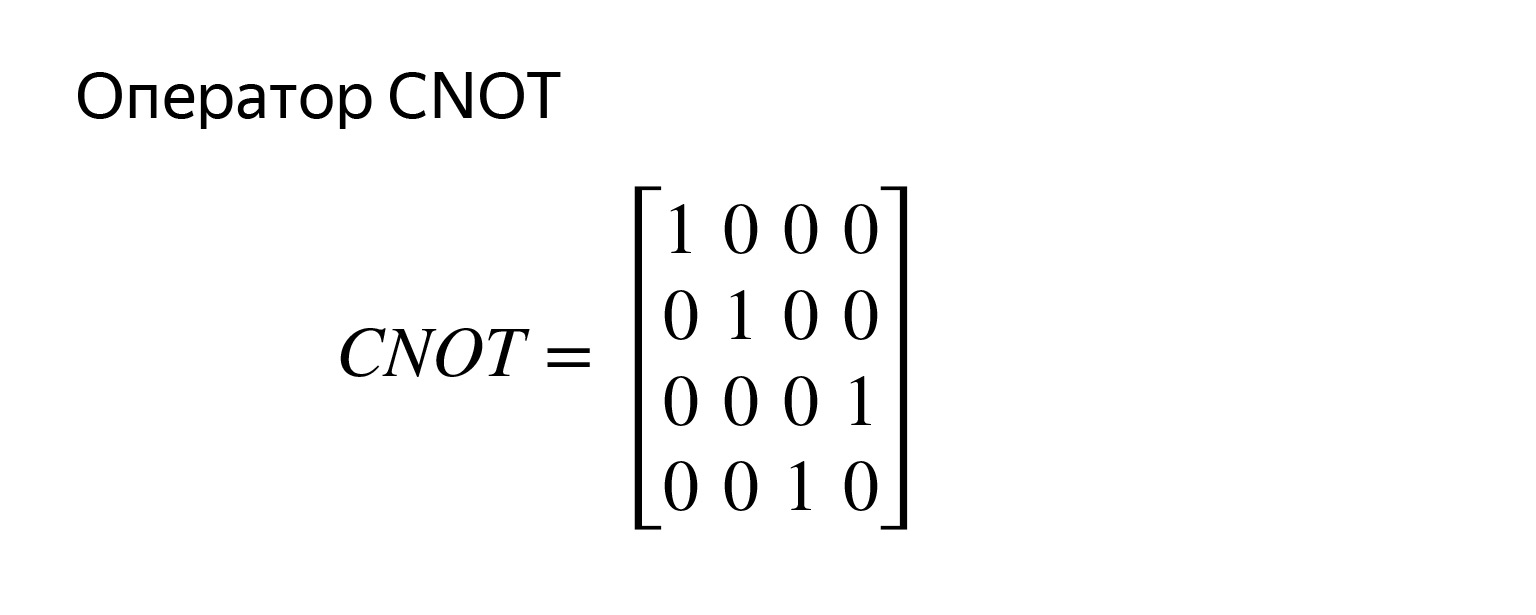
Matriksnya sudah empat kali empat. Untuk dua qubit, sepertinya ini. Saya akan meninggalkan masalah dengan tanda bintang untuk berkembang biak dan melihat apakah ini benar.

Hal ini bahkan dapat diprogram. Tidak ada ilmu roket. Anda hanya perlu mengambil, membuat sirkuit dengan dua qubit, dengan dua yang klasik, dan jangan, bukan hanya CNOT, tetapi CX, negasi yang dikendalikan.
Negasi adalah operator X, jadi pada prinsipnya semuanya logis. Dan Anda bisa menggambar diagram. Skemanya adalah sebagai berikut.
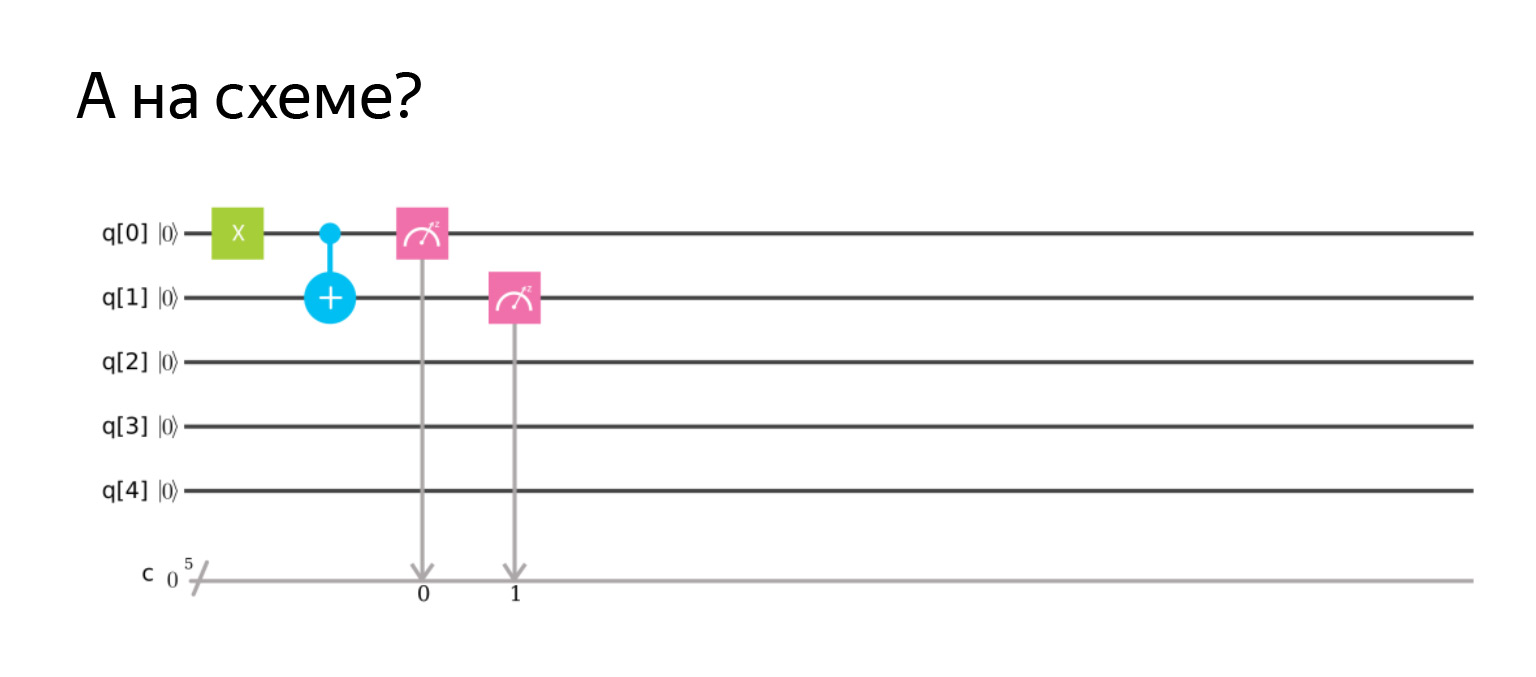
Artinya, negasi terkontrol adalah nilai tambah pada qubit yang ingin kita ubah. Dan intinya, yang merupakan kontrol. Di sini, jika qubit bersatu, maka kita akan mengubah yang kedua.

Di sini saya secara khusus membalikkan yang pertama sehingga menjadi satu, dan kemudian saya mengukur keduanya dan mendapatkan hasilnya | 11⟩. Semuanya seperti yang kita harapkan.
Tapi sekarang saatnya menggunakan semua pengetahuan kita bersama.

Mari kita ambil ketiga atau empat operator yang kita tahu, dan tempelkan ke satu skema. Artinya, kami menerapkan operator Hadamard ke operator pertama. Balikkan yang kedua, lalu bersama-sama, lakukan negasi dan ukuran yang terkontrol.
Mari kita belum menjalankannya, tetapi coba tebak apa yang akan terjadi.
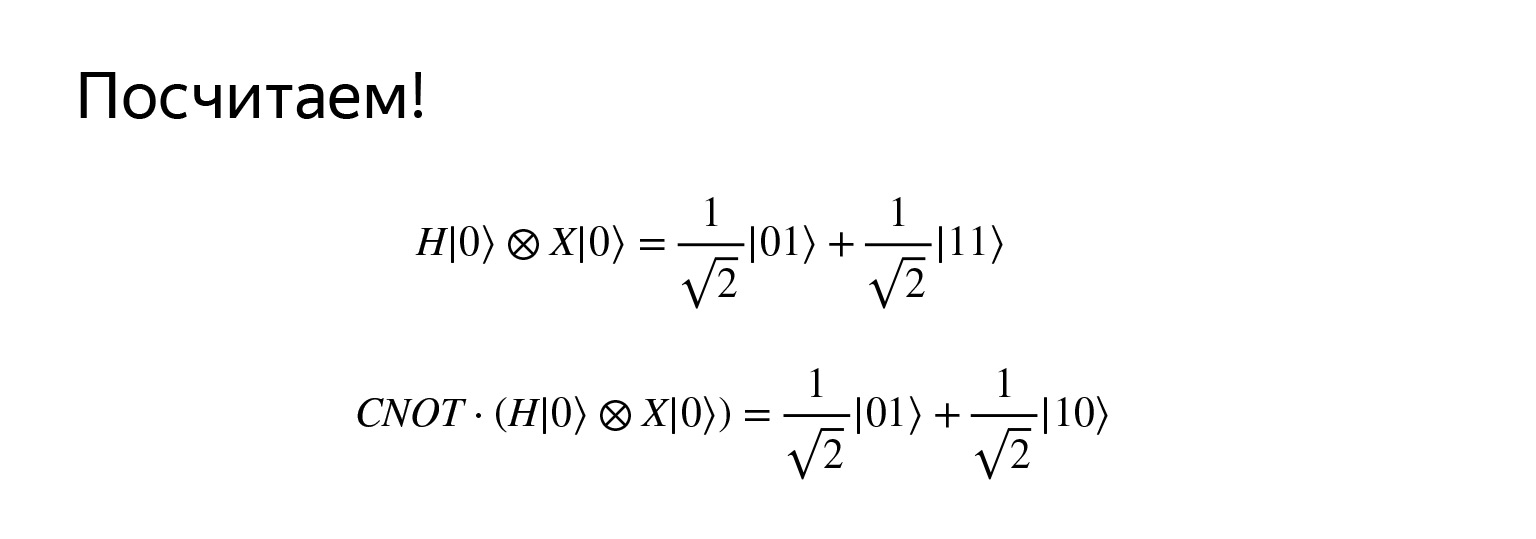
Jika kita menerapkan operator Hadamard ke qubit pertama, dan meniadakan yang kedua, maka kita mendapatkan superposisi seperti itu. Saya tidak ingin membuang waktu untuk memeriksa sekarang, ini dapat dengan mudah dikalikan. Namun posisinya sangat menarik. Pertama, sangat mirip dengan seragam, dan, kedua, sekarang negara ini disebut terjerat, jika kita juga mengambil negasi terkontrol.

Negara membingungkan. Dan mengapa? Mari kita coba melakukan pengukuran. Dengar, jika saya mengukur qubit pertama dan saya memilikinya dalam keadaan nol, maka saya dapat mengatakan bahwa qubit kedua harus dalam keadaan satu.
Yaitu, jika saya melakukan transformasi seperti itu dengan qubit saya, saya memberikan satu qubit kepada teman saya, dia akan terbang ke New York, dan saya mengukur qubit kedua pada diri saya sendiri, saya akan tahu persis bagaimana keadaan qubitnya. Ini disebut efek keterikatan kuantum atau keterhubungan kuantum. Dan ini adalah mekanisme utama dimana komputasi kuantum bekerja. Ini akan berubah, mereka terhubung dengan sangat kaku, dan selama pengukuran kita hanya bisa mendapatkan | 00⟩ atau | 11⟩.
Pada kesempatan ini, ada ilustrasi yang sangat menarik yang mendukung seorang ilmuwan, Austria, menurut pendapat saya,

Gangguannya adalah dia mengenakan kaus kaki yang berbeda sepanjang waktu. Dan rekan-rekannya bercanda tentang dia: jika dia memasuki ruangan dengan satu kaki dan kita melihat bahwa kaus kaki itu berwarna merah muda, maka kita dapat mengatakan bahwa kaus kaki yang kedua bukan merah muda. Begitu seterusnya.
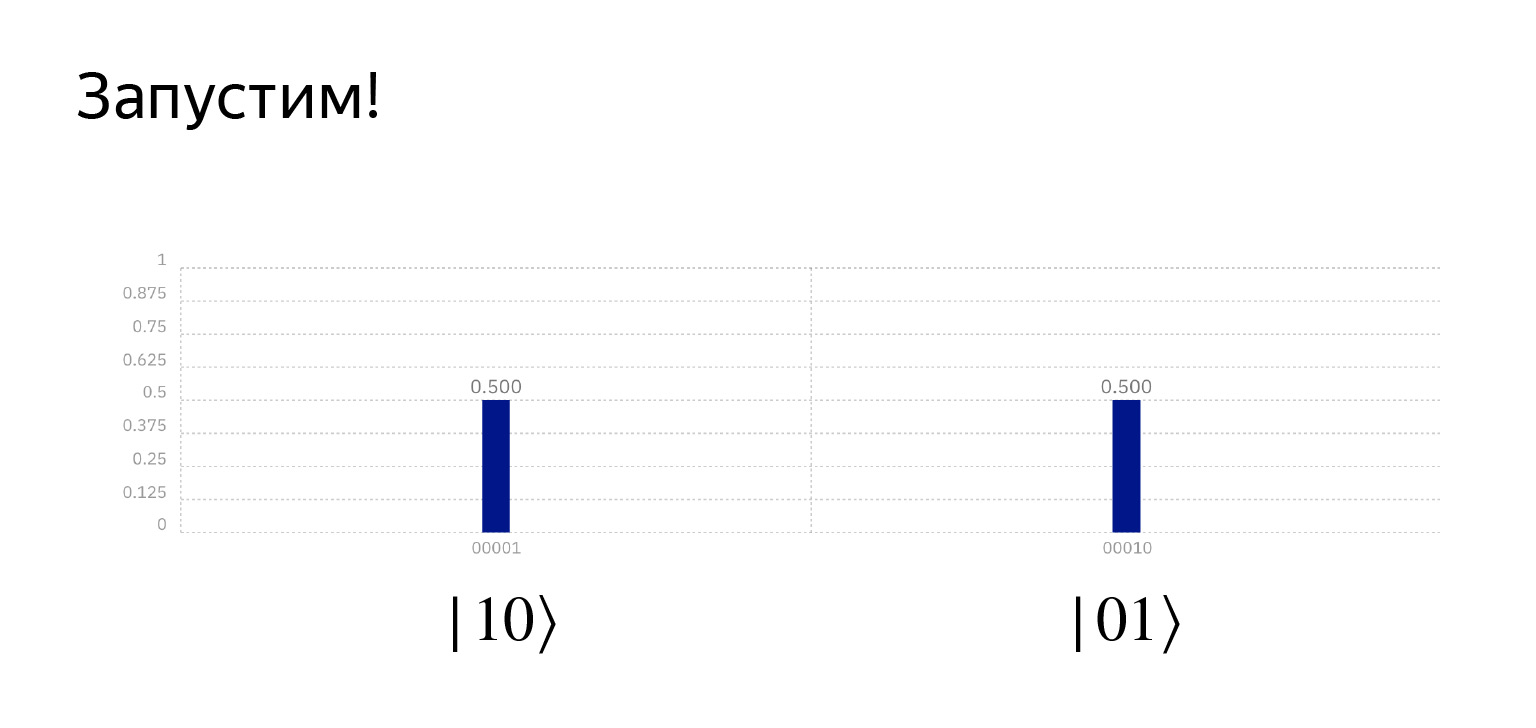
Jika kita menjalankan hal ini, kita mendapatkan apa yang kita inginkan. Sudah cukup lucu di sini. Probabilitasnya tepat 0,5, tapi ini kebetulan.
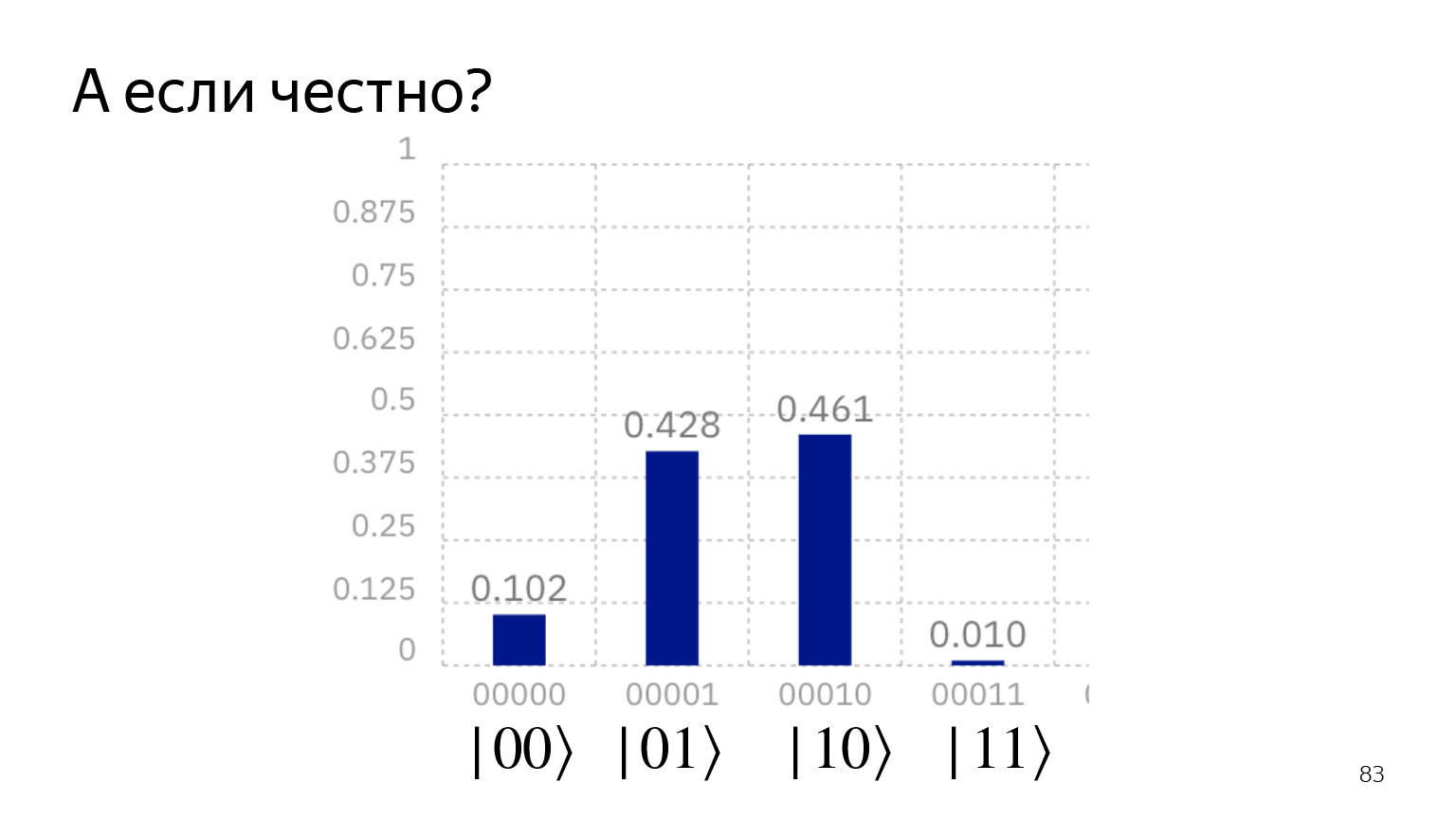
Jika kita menjalankan komputer kuantum dengan jujur, kita mendapatkan gambar ini. Kami sepertinya mengatakan: negara | 00⟩ tidak pernah dapat diperoleh dan negara | 11⟩ tidak pernah bisa diperoleh. Tetapi masih berfungsi: keadaan teknologi saat ini sedemikian rupa sehingga ada suara yang tidak selalu mudah ditekan. Dan mereka berjuang dengan ini.
Tetapi jika Anda ingat ilmu komputer klasik, itu hal yang sama: kode koreksi kesalahan dan semua itu. Hanya saja qubit terlalu kecil untuk saat ini untuk menghabiskan bit tambahan pada koreksi kesalahan.
Sekarang, seperti yang saya janjikan, beberapa contoh algoritma. Tapi ini hanya akan menjadi contoh tanpa dasar analisis algoritma, sehingga Anda melihat, berpikir, menjadi tertarik.

Algoritma pertama hanya terkait dengan Deutsch, yang telah kita bicarakan di awal. Ini adalah algoritma Deutsch-Jozy. Dan dia melakukan yang berikut. Bayangkan kita memiliki fungsi Boolean dalam n variabel. Dan kita tahu pasti bahwa itu konstan atau seimbang. Seimbang berarti bahwa pada setengah dari argumen itu sama dengan nol, dan pada setengah lainnya - ke satu. Mari kita coba untuk memeriksa secara klasik apakah konstan atau tidak.
Untuk melakukan ini, kita perlu memeriksa setidaknya setengah dari semua opsi yang mungkin: opsi 2 n - 1 +1. Algoritma kuantum memungkinkan Anda untuk melakukan ini dalam n panggilan ke fungsi itu sendiri, dalam n perhitungan fungsi itu sendiri. Ini adalah jumlah hit yang secara eksponensial lebih rendah.
Contoh kedua mungkin diketahui oleh semua orang, karena itu mereka mengatakan bahwa komputer kuantum akan menghancurkan semua kriptografi: kita dapat memfaktorkan bilangan kuantum dengan sangat cepat.

Perkiraan kesulitan diberikan di sini dan ada contoh yang fantastis. Pada 2011, angka 15 difaktorkan di komputer sungguhan. Butuh tujuh qubit.

Tapi tidak semuanya buruk. Jika komputer kuantum mencapai tingkat di mana Anda dapat memecahkan RSA, sudah ada kriptografi pasca-kuantum. Itu dibangun di atas pembelajaran dengan kesalahan. Ini adalah ketika kesalahan kecil dimasukkan ke dalam masalah sehingga sangat sulit untuk menemukan jawaban. Biasanya ini adalah semacam persamaan atau sistem persamaan. Berikut ini contoh algoritma. Siapa pun yang ingin dapat membaca lebih detail.
Paling menarik: algoritma Harapan Baru didasarkan pada hal ini , harapan baru semua umat manusia. Pada 2016, Chrome menambahkan dukungan untuk algoritma ini. Ada tautan ke blog di sini. Ini bukan ide saya, semuanya sebenarnya. Masa depan sudah ada di sini.
Ada beberapa tautan di akhir:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
Ini kurang lebih semuanya. Saya hanya ingin menambahkan itu sekitar 50 tahun yang lalu, ketika Deutsch mulai melakukan ilmu informasi kuantum, komputer itu besar. Mereka dibuat oleh beberapa perusahaan. Mereka seukuran lemari pakaian. Dan sekarang, kira-kira perusahaan yang sama membuat komputer kuantum besar. Dan, tentu saja, kita tidak tahu apa yang akan terjadi dalam 50 tahun.
Jika Anda mencoba mengetik di mesin pencari favorit Anda, maka hari ini Anda dapat menemukan lowongan untuk seorang programmer kuantum. Tentu, ada lebih banyak penelitian di luar sana, namun demikian. Terima kasih