
Optimalisasi dalam bisnis di sebagian besar kasus dikaitkan dengan penggunaan metode pemrograman linier. Metode ini cukup mudah. Selain itu, ada teorema tentang keberadaan dan keunikan solusinya.
Namun, dalam praktiknya, semuanya tidak sepenuhnya sederhana.
Masalah pertama adalah ketidaklinieran kondisi dunia nyata. Agar metode pemrograman linier dapat diterapkan, mereka harus dilinearisasi. Ada beberapa cara pengaturan nonlinier yang masuk akal melalui persamaan dan ketidaksetaraan linear dengan memperkenalkan variabel baru, menetapkan koefisien bobot, dll. Ketika memecahkan masalah produksi dalam hal ini, perlu untuk beroperasi dengan sejumlah besar variabel dan, dengan demikian, persamaan (ketidaksetaraan).
Dalam teori pemecahan masalah ekstrem, ada teorema tentang stabilitas solusi untuk masalah pemrograman linier. Menurutnya, solusinya stabil hanya jika domain masalahnya adalah cembung. Dengan sejumlah besar variabel dan ketidaksetaraan, tidak mungkin menentukan apakah domain masalahnya cembung. Selain itu, probabilitas non-konveksitas tinggi.
Jika masalahnya tidak stabil, maka tergantung pada titik awal melintasi simpul, hasil yang berbeda akan diperoleh.
Masalah kedua- pembatasan variabel dari bawah (x> h> 0). Setiap implementasi metode pemrograman linier akan selalu memberikan nilai x tidak nol. Jika x persis sama dengan h, maka ini berarti bahwa nilai variabel x pada dasarnya harus nol. Dalam praktiknya, volume "fiktif" seperti itu (metode kurtosis) tersebar di variabel "bermakna". Konsekuensi dari praktik ini adalah erosi konsep solusi optimal, yang sangat penting jika solusi tersebut adalah salah satu dari banyak dalam rantai keputusan.
Masalah ketiga adalah manajerial. Metode pemrograman linier hanya memberikan satu hasil. Dan bagaimana cara melihat hasil yang mendekati optimal? Misalnya, dalam solusi yang dihasilkan, peringkat vendor buruk. Bagaimana memahami jika ada solusi yang dekat, tetapi untuk pemasok yang dapat diandalkan.
Tugas pengangkutan
Contohnya sesuai dengan masalah pemrograman linear transportasi.
Ada 5 operator (tugas ditetapkan untuk pengangkutan batu bara), yang memiliki dua perhitungan tarif. Batas-batas tarif dan tarif itu sendiri dapat diubah (ditetapkan secara parametrik).

Transportasi ditentukan sebagai point-to-point (sesuai dengan metode yang diterima untuk transportasi batubara) dan volume.
Tampilan umum antarmuka.

Area penugasan transportasi.
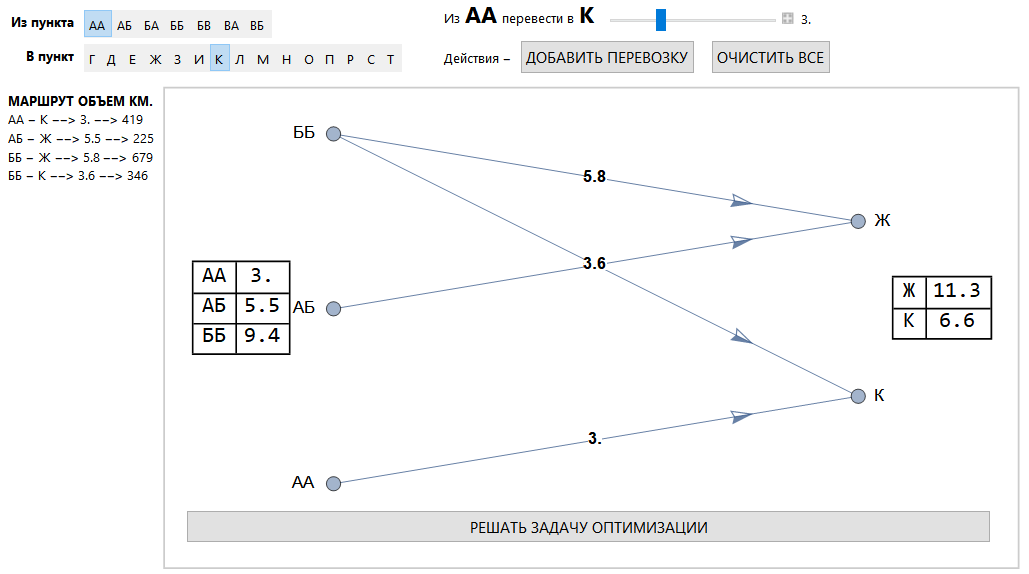
Metode solusi cluster
Alih-alih satu masalah pemrograman linier, sekelompok masalah diselesaikan, jumlah yang sesuai dengan semua kemungkinan kombinasi tarif. Dalam pengiriman di atas, ada 127 di antaranya (nilai kedua di persegi panjang kiri atas).

Solusi optimal dipilih dari serangkaian masalah yang benar yang tersisa. Setiap tugas memberikan solusi optimal untuk kombinasi tarif tertentu. Solusi yang disajikan di atas merupakan kisaran maksimum tertentu.
Mengapa metode cluster bagus:
- pemahaman tentang stabilitas solusi muncul.
- tidak ada volume "fiktif" untuk variabel yang dibatasi dari bawah, karena akan ada kombinasi lain di mana kondisi seperti itu tidak ada (karena variabel seperti itu tidak ada).
- kondisi subyektif (peringkat, preferensi) dapat diperkenalkan menggunakan metode pemrograman linier standar.
Dengan jumlah pengiriman yang lebih besar, kami memiliki gambar berikut (fragmen).
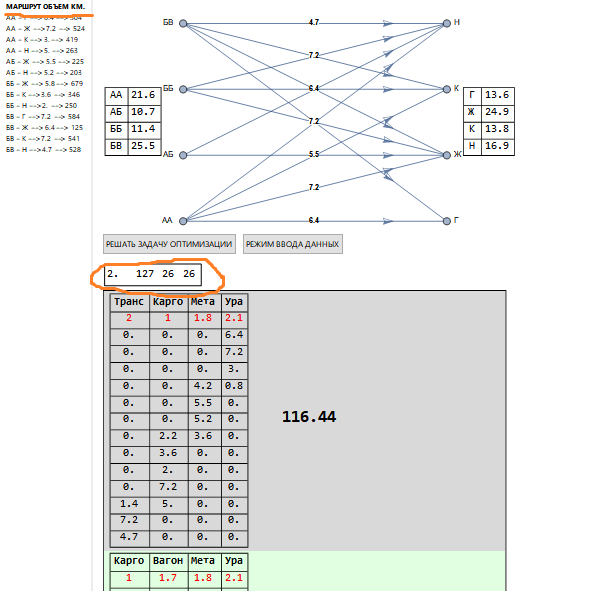
Di sudut kiri atas, dalam persegi panjang di atas solusi (disorot dalam oranye), nilai-nilai lain ditunjukkan dari sebelumnya: 127 - kombinasi (seperti sebelumnya, yang terkait dengan struktur skala tarif), 26 - sesuai dengan jumlah masalah yang benar yang tersisa yang sedang diselesaikan. Tarif yang digunakan ditunjukkan dengan warna merah di bawah nama operator, dan kolom transportasi sesuai dengan daftar rute (bergaris oranye).
Penting untuk dicatat bahwa metode yang digunakan memungkinkan Anda untuk memahami hasilnya, mengevaluasi solusi serupa dan menggunakan pengalaman profesional Anda ketika memilih alternatif, dengan mempertimbangkan seluk-beluk menjalankan bisnis tertentu.