Deteksi tabrakan dan teorema sumbu pemisah

Saat ini, komputer adalah komputer yang kuat yang

mampu melakukan jutaan operasi per detik. Dan tentu saja, Anda tidak dapat melakukannya tanpa simulasi dari dunia nyata atau game. Salah satu masalah pemodelan dan simulasi komputer adalah menentukan tumbukan dua objek, salah satu solusi yang diwujudkan oleh teorema pada sumbu pemisah.







Catatan. Artikel ini akan memberikan contoh dengan 2 parallelepipeds (selanjutnya - kubus), tetapi ide untuk objek cembung lainnya akan dipertahankan.

Catatan. Semua implementasi akan dilakukan di Unity.

Babak 0. Teori umum

Pertama, Anda harus berkenalan dengan " teorema pemisahan hyperplane ". Ini akan menjadi dasar dari algoritma.



Dalil. Dua geometri cembung tidak berpotongan jika dan hanya jika ada hyperplane di antara mereka yang memisahkan mereka. Sumbu ortogonal ke

hyperplane pemisah disebut sumbu pemisah, dan proyeksi angka-angka di atasnya tidak berpotongan.





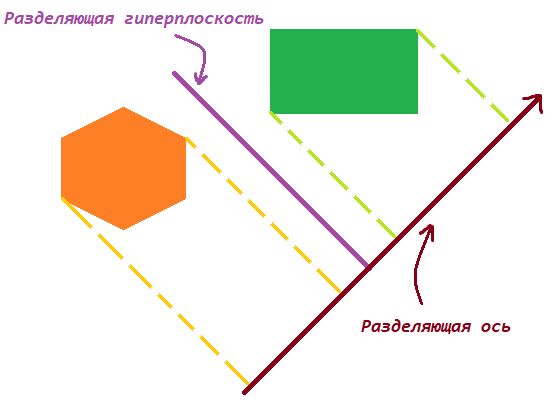
Dividing axis (case 2D)





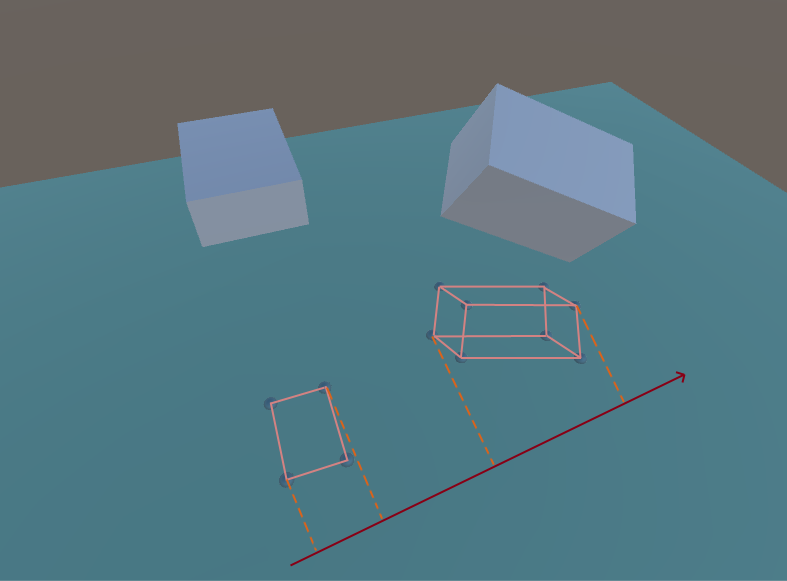
Dividing axis (case 3D)

Anda mungkin memperhatikan bahwa proyeksi pada sumbu pembagian tidak berpotongan.



Properti. Sumbu pemisah potensial adalah dalam set berikut:

• Norma bidang setiap kubus (merah)
• Produk vektor dari tepi kubus $$$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$,

   di mana X adalah tepi kubus pertama (hijau) dan Y adalah yang kedua (biru).







Kami dapat menjelaskan setiap kubus dengan data input berikut:

• Koordinat pusat kubus
• Dimensi kubus (tinggi, lebar, kedalaman)
• Kuota kubus

Mari kita buat kelas tambahan untuk ini, contoh yang akan memberikan informasi tentang kubus.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

Act 1. Quaternions

Seperti yang sering terjadi, suatu objek dapat berputar di ruang angkasa. Untuk menemukan koordinat simpul, dengan mempertimbangkan rotasi kubus, Anda perlu memahami apa angka empat itu.



Quaternion adalah angka hypercomplex yang menentukan rotasi suatu objek di ruang angkasa.

$$

$$w+xi+yj+zk$$

Bagian imajiner (x, y, z) mewakili vektor yang menentukan arah rotasi,

bagian nyata (w) mendefinisikan sudut di mana rotasi akan dilakukan.



Perbedaan utamanya dari semua sudut Euler yang biasa adalah bahwa cukup bagi kita untuk memiliki satu vektor, yang akan menentukan arah rotasi, daripada tiga vektor bebas linear yang memutar objek dalam 3 subruang.



Saya merekomendasikan dua artikel yang lebih rinci tentang angka empat:



Satu

Dua



Sekarang kita memiliki pemahaman minimal angka empat, mari kita memahami cara memutar vektor dan menggambarkan fungsi memutar vektor dengan angka empat.



Formula rotasi vektor

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$$\vec{v}'$ Apakah vektor yang diperlukan

$$$\vec{v}$ - vektor asli

$$$q$ - angka empat

$$$\overline{q}$- angka empat terbalik



Untuk mulai dengan, mari kita memberikan konsep angka empat terbalik dalam basis ortonormal - itu adalah angka empat dengan bagian imajiner dari tanda yang berlawanan.



$$$q = w+xi+yj+zk$

$$$\overline{q} = w-xi-yj-zk$



Mari berhitung $$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



Sekarang kita akan menuliskan masing-masing komponen dan dari produk ini kita akan mengumpulkan angka empat baru

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



Mari kita hitung sisanya, mis. $$$q*M$dan dapatkan vektor yang diinginkan.



Catatan. Agar tidak membebani perhitungan, kami hanya menyajikan bagian imajiner (vektor) dari produk ini. Bagaimanapun, dialah yang mencirikan vektor yang diinginkan.



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



Mari mengumpulkan komponen-komponen vektor



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

Dengan demikian, vektor yang diperlukan diperoleh. Tulis



kode:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

Babak 2. Menemukan simpul-simpul sebuah kubus

Mengetahui cara memutar vektor dengan angka empat, tidak akan sulit untuk menemukan semua simpul kubus.



Mari kita beralih ke fungsi menemukan simpul dari sebuah kubus. Mari kita mendefinisikan variabel dasar.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

Selanjutnya, Anda perlu menemukan titik (anchor point) yang darinya akan lebih mudah untuk menemukan simpul lainnya.



Kurangi setengah dimensi kubus dari pusat secara bersamaan, lalu tambahkan satu dimensi kubus ke titik pivot.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

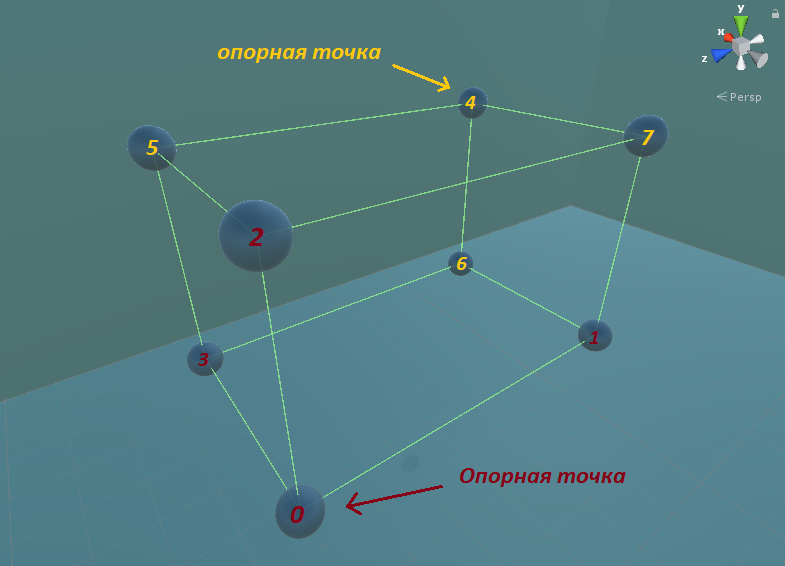
Kita dapat melihat bagaimana titik-titik terbentuk



Setelah menemukan koordinat simpul, perlu untuk memutar setiap vektor dengan angka empat yang sesuai.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

Mari beralih ke proyeksi.

Babak 3. Mencari kapak pemisah

Langkah selanjutnya adalah menemukan himpunan sumbu yang mengklaim dapat membelah.

Ingatlah bahwa itu dapat ditemukan di set berikut:

• Normal pesawat setiap kubus (merah)
• Produk vektor dari tepi kubus $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$di mana X adalah tepi kubus pertama (hijau) dan Y adalah yang kedua (biru).

Untuk mendapatkan sumbu yang diperlukan, cukup memiliki empat simpul kubus, yang membentuk sistem vektor ortogonal. Verteks ini berada dalam empat sel pertama dari array titik yang kita bentuk pada aksi kedua.







Hal ini diperlukan untuk menemukan normal pesawat yang dihasilkan oleh vektor:

• $$$\vec{a}$ dan $$$\vec{b}$
• $$$\vec{b}$ dan $$$\vec{c}$
• $$$\vec{a}$ dan $$$\vec{c}$

Untuk melakukan ini, perlu untuk mengulangi melalui pasang tepi kubus sehingga setiap sampel baru membentuk bidang ortogonal untuk semua bidang yang diperoleh sebelumnya. Sangat sulit bagi saya untuk menjelaskan cara kerjanya, jadi saya telah menyediakan dua versi kode untuk membantu Anda memahami.





Tetapi Anda dapat membuatnya lebih mudah:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

Kami juga harus menemukan semua produk vektor dari tepi kubus. Ini dapat diatur dengan pencarian sederhana:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

Act 4. Proyeksi pada sumbu

Kami telah sampai pada titik paling penting. Di sini kita harus menemukan proyeksi kubus pada semua sumbu pemisah yang potensial. Teorema ini memiliki satu konsekuensi penting: jika benda berpotongan, maka sumbu yang memotong proyeksi proyeksi kubus adalah minimal adalah arah (normal) tabrakan, dan panjang segmen persimpangan adalah kedalaman penetrasi.



Tapi pertama-tama, ingat rumus untuk proyeksi skalar vektor v ke vektor satuan a :

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

Sekarang kita akan menjelaskan fungsi yang akan menentukan persimpangan proyeksi pada sumbu kandidat.



Input adalah simpul dari dua kubus, dan daftar sumbu pemisah yang potensial:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

Proyeksi ke sumbu diatur oleh dua titik yang memiliki nilai maksimum dan minimum pada sumbu itu sendiri:







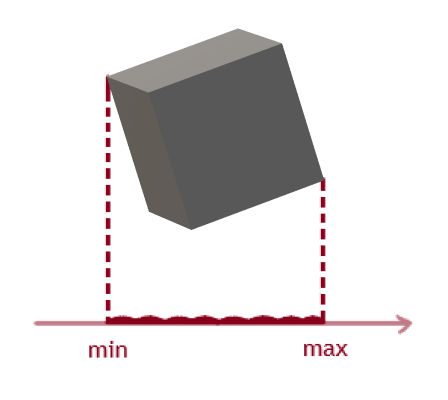
Selanjutnya, kami membuat fungsi yang mengembalikan titik proyeksi setiap kubus. Dibutuhkan dua parameter pengembalian, array verteks dan sumbu pemisah potensial.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

Jadi, menerapkan fungsi ini ( ProjAxis ), kami mendapatkan poin proyeksi dari setiap kubus.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

Selanjutnya, berdasarkan pada simpul proyeksi, kita menentukan persimpangan dari proyeksi:







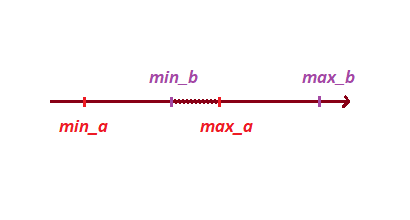
Untuk melakukan ini, mari kita taruh poin kita ke dalam array dan mengurutkannya, metode ini akan membantu kita menentukan tidak hanya persimpangan, tetapi juga kedalaman persimpangan.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

Perhatikan properti berikut:



1) Jika segmen tidak bersinggungan , maka jumlah segmen akan lebih kecil dari segmen dengan titik ekstrim yang terbentuk:







2) Jika segmen berpotongan , maka jumlah segmen akan lebih besar daripada segmen dengan titik ekstrem yang terbentuk:







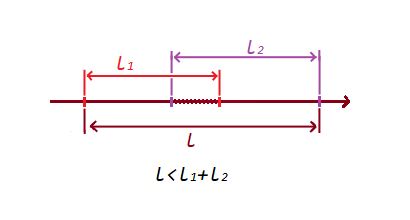
Dengan kondisi sederhana ini, kami memeriksa persimpangan dan non-persimpangan segmen.



Jika tidak ada persimpangan, maka kedalaman persimpangan akan menjadi nol:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

Dengan demikian, cukup bagi kita untuk memiliki setidaknya satu vektor di mana proyeksi kubus tidak berpotongan, maka kubus itu sendiri tidak berpotongan. Oleh karena itu, ketika kami menemukan sumbu pemisah, kami dapat melewati pemeriksaan vektor yang tersisa dan menghentikan algoritme.



Dalam kasus persimpangan kubus, semuanya sedikit lebih menarik: proyeksi kubus pada semua vektor akan berpotongan, dan kita harus mendefinisikan vektor dengan persimpangan minimum.



Mari kita buat vektor ini sebelum loop, dan kita akan menyimpan vektor dengan panjang minimum di dalamnya. Jadi, pada akhir siklus, kita mendapatkan vektor yang diinginkan.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

Dan setiap kali kami menemukan sumbu di mana proyeksi berpotongan, kami memeriksa apakah itu adalah yang terkecil di antara semuanya. kita mengalikan sumbu tersebut dengan panjang persimpangan, dan hasilnya akan menjadi normal (arah) dari persimpangan kubus.



Saya juga menambahkan definisi orientasi normal sehubungan dengan kubus pertama.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

Kesimpulan

Proyek dengan implementasi dan contoh diunggah ke GitHub, dan Anda dapat melihatnya di sini .



Tujuan saya adalah untuk berbagi pengalaman saya dalam memecahkan masalah yang terkait dengan menentukan persimpangan dua objek cembung. Dan juga dapat diakses dan dimengerti untuk menceritakan teorema ini.