
Artikel lain dalam siklus
Pada bagian IV ini, kami melengkapi uraian sandi AES - 128. Bagi pembaca yang tidak terbiasa dengan bagian pekerjaan sebelumnya, saya akan menjelaskan bahwa materi tersebut disajikan untuk tujuan pendidikan dan ini memaksakan sejumlah fitur (perincian, contoh angka, dasar matematika, dll.) Ini tidak hanya dimaksudkan untuk membiasakan diri dengan standar. , dan penggunaan materi yang disajikan untuk pengembangan algoritma enkripsi dan dekripsi (dengan tidak adanya kunci). Para penulis dari banyak publikasi online (dan offline) yang terkenal tidak menetapkan sendiri tujuan tersebut, yang menjadikan publikasi ini sedikit digunakan untuk tujuan kita.
Proses sebaliknya dari enkripsi disebut dekripsi pesan. Untuk mendekripsi (dengan kunci) ciphertexts (ST), dibuat tabel substitusi terbalik dan kunci bulat, yang digunakan dalam urutan terbalik relatif terhadap skema enkripsi, tetapi serupa dengan proses enkripsi.
Mengurai Pesan AES
Daftar operasi untuk mendekripsi pesan tetap sama dengan untuk enkripsi. Rincian lebih lanjut tentang operasi dapat ditemukan di sini . Ini adalah prinsip cipher yang cukup umum - implementasi perangkat keras tunggal untuk enkripsi dan dekripsi, yang disediakan oleh serangkaian fungsi yang sama untuk kedua proses. Hanya teks sumber dan urutan pengiriman kunci yang diubah.
Proses mendekripsi pesan diimplementasikan sebagai urutan transformasi terbalik (terbalik) yang digunakan untuk enkripsi, dalam urutan terbalik urutannya selama enkripsi. Juga jelas bahwa tombol bulat digunakan dalam urutan yang sesuai: pertama, kunci diterima terakhir, lalu kunci kedua dari belakang, dan seterusnya sampai kunci putaran pertama.
Semua nama transformasi tetap sama, tetapi diawali dengan Inv. Kami akan mempertimbangkan mereka dalam urutan yang sama seperti sebelumnya. Cipher AES memungkinkan dua opsi dekripsi, mundur dan maju, yang dibahas secara rinci di bawah ini.
Membalikkan opsi dekripsi
Membalik dekripsi pesan adalah proses alami membalikkan proses enkripsi.
Operasi AddRoundKey tetap sama (tidak berubah) S + Ki untuk semua 16 byte negara seperti yang terjadi ketika mengenkripsi pesan, yaitu adalah kebalikan dari dirinya sendiri. Ini disebabkan oleh fakta bahwa logika XOR digunakan dalam operasi, dan byte dapat direpresentasikan dalam bilangan biner.
Kunci putaran terakhir cukup ditambahkan (disimpulkan) ke pesan terenkripsi.
InvSubBytes. Inti dari transformasi ini tidak berubah, yaitu, setiap byte pesan yang dikonversi diganti dengan yang lain yang diambil dari tabel (S -1-block) penggantian. Tentu saja, tabel substitusi berbeda di sini. Byte {x, y} diganti oleh byte dari Inv S (x, y) sesuai dengan prinsip yang sama: x - baris tabel, y - kolomnya. Byte pengganti diambil dari sel di persimpangan baris (x) dan kolom (y) dari tabel Inv S (x, y).
Seperti sebelumnya, ukuran tabel adalah 16 × 16 = 256 byte, yang masing-masing diperoleh dengan perkalian dan pengurangan vektor-matriks (transformasi affine) dari produk vektor shift C. Dalam bidang biner, operasi penambahan dan pengurangan adalah setara, sehingga vektor C dapat dengan mudah ditambahkan ke produk. Tabel InvSubBytes ditunjukkan di bawah ini. Node tertentu dari substitusi S -1 disajikan dalam tabel 1 berikut, nilainya diberikan dalam format heksadesimal:
Tabel 1. Tabel substitusi dari blok S -1 - terbalik

Tabel menunjukkan contoh penggantian dua byte 4A → 5C dan 9F → 6E yang diisi dengan warna hijau.
InvShiftRows. Transformasi ini menggeser baris dalam tabel (alun-alun Negara) ke kanan (ke arah yang berlawanan dengan pergeseran asli). Nilai pergeseran untuk setiap baris tetap sama: baris pertama (atas) tidak bergeser c0 = 0, yang kedua digeser oleh c1 = 1, yang berikutnya digeser oleh c2 = 2, dan yang terakhir adalah c3 = 3 posisi (sel). Nilai-nilai c0, c1, c2, c3 diberikan dalam tabel dan pada gambar sebelumnya untuk putaran pertama konversi pesan.

Hasil dari penggandaan seperti itu dalam representasi skalar adalah:
S'0C = ({0l} · S0C) {({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C);
S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);
S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);
S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).
Untuk mendapatkan IT dari PC, algoritma dekripsi menggunakan nilai parameter yang sama yang digunakan dalam proses enkripsi. Untuk pembentukan kunci yang diperluas, aturannya tetap sama.
Opsi dekripsi langsung
Keunikan algoritma dekripsi untuk beberapa transformasi terbalik memungkinkan untuk mempertahankan urutan operasi yang sama seperti pada algoritma enkripsi, tetapi beberapa nilai parameter memerlukan perubahan. Pertama-tama, kita berbicara tentang kunci (yang terbuka).
Penelitian telah menunjukkan bahwa urutan fungsi SubBytes () dan ShiftRows () tidak mengubah nilai hasil, yaitu, fungsi-fungsi ini diijinkan (mereka bolak-balik). Posisi ini (properti) juga berlaku untuk fungsi InvSubBytes (), InvShiftRows (). Pola ini mudah dijelaskan. Intinya adalah bahwa kedua fungsi beroperasi pada byte integer, dan pergeseran dilakukan oleh kelipatan integer byte, dan tidak mengubah nilai byte itu sendiri.
Perhatikan hal berikut tentang operasi MixColumns (). Ini linier ke byte input (data).
InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR
InvMixColumns (Round Key).
Fitur-fitur fungsi (properti) ini memungkinkan perubahan urutan aplikasi mereka, yaitu
InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).
AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),
tetapi asalkan kolom (32-bit kata-kata) dari kunci dekripsi diperluas sebelumnya dilewatkan melalui fungsi
InvMixColumns ().
Hal tersebut di atas berarti bahwa cara dekripsi PC dapat dibuat efektif dengan menjaga urutan penggunaan fungsi yang diadopsi untuk enkripsi. Jelas, dalam hal ini, biaya implementasi perangkat keras dan lunak dari cipher berkurang secara signifikan. Perubahan hanya menyangkut prosedur untuk menghasilkan penyebaran kunci.
Dalam fungsi InvMixColumns (), Anda perlu mengkonversi jenis variabel, parameter input dari fungsi adalah array byte dua dimensi (persegi), dan kunci yang diperluas dibentuk sebagai array (string) linear dari 32-bit kata. Untuk alasan ini, perlu untuk melakukan pencocokan tipe ke kotak.
Mari kita tunjukkan, menggunakan contoh transformasi 2-putaran, dua versi yang setara dari prosedur dekripsi RIJNDAEL. Opsi pertama adalah kebalikan dari fungsi enkripsi yang biasa. Opsi kedua diperoleh dari yang pertama dengan mengubah urutan operasi dalam tiga pasang transformasi
InvShi ftRows () → InvSubBytes () 2 kali dan
AddRoundKey () → InvMixColumns () 1 kali.
Hasil transformasi disimpan ketika melewati dari aslinya ke
urutan terbalik dari operasi dalam pasangan yang ditentukan.
Dari tabel kita melihat bahwa prosedur enkripsi dan varian kedua dari prosedur dekripsi bertepatan dengan urutan menggunakan tombol bulat (ketika melakukan operasi AddRoundKey), tabel penggantian (saat melakukan operasi SubBytes () dan InvSubBytes ()) dan matriks transformasi (saat melakukan MixColumns ( ) dan InvMixColumns ()).
Tabel 2 - Urutan transformasi dalam versi dua putaran RIJNDAEL

. Hasil serupa ternyata benar untuk sejumlah putaran.
Memulihkan kunci sandi menggunakan subkunci terakhir
Pembuatan kunci sandi AES putaran. Jadwal Kunci untuk menghasilkan kunci bulat dari kunci sandi 128-bit asli adalah fungsi rekursif. Fungsi ini dibahas secara rinci di sini . Kondisi awal untuk peluncurannya adalah 4 4 byte pertama kata kunci (4 × 32-bit words), yaitu W [0], W [1], W [2], W [3].
Mari kita merumuskan masalah memulihkan kunci sandi 128-bit ini sebagai berikut: Biarkan komponen-komponen dari kunci putaran 10 W (43), W [42], W [41], W [40] ditemukan.
Diperlukan untuk memulihkan kunci sandi penuh dengan hanya kunci putaran ini.
Lebih mudah untuk mempertimbangkan solusi untuk masalah pertama pada data numerik. Mari kita ambil contoh angka yang diberikan dalam FIPS PUB 197 sebagai dasar.. Tabel 3 berisi tombol bulat 10.
Prosedur untuk menghasilkan kunci bundar diatur sedemikian rupa sehingga memberikan gerakan maju (membuka kunci) di sepanjang sejumlah nilai kunci sebelumnya. Untuk bergerak mundur dari beberapa titik dari serangkaian nilai, perlu memiliki data awal dari proses perhitungan pada titik pengembalian ini. Biarkan titik pengembalian menjadi langkah terakhir dari ronde 10 terakhir, mis., Empat kata 4-byte dari kunci ronde 10 Nk = Nb = 4 diketahui.
Tabel 3 - Kunci 128-bit dari putaran 10 cipher AES

Selanjutnya, hasil dan tindakan dari algoritma pemulihan kunci ditempatkan untuk kenyamanan ke tabel 4, yang mirip dengan tabel generasi kunci (semacam terbalik).
Tabel 4 - Pemulihan kunci sandi dari kunci putaran ke-10 yang diketahui

Penjelasan untuk Tabel 4. Angka bulat dihitung dalam urutan terbalik dari tanggal 10 hingga tanggal 1. Tiga kolom (3, 8, 9) dari tabel berisi kunci siap pakai dengan nomor saat ini berbeda tergantung pada nomor baris i. Sel-sel yang tersisa berisi data tambahan untuk perhitungan menengah. Dengan demikian, nilai kunci W [i] muncul dalam tabel tiga kali dalam tiga kolom.
Kolom 1 dan 2 adalah angka r dari putaran dan nomor urut dari kata kunci 4-byte. Kata seperti terakhir selama enkripsi memiliki angka i = 43. Dalam tabel kita menuliskannya di baris paling atas kolom (9) kanan. Nomor baris i pada tabel menurun dan pada kolom 9 angka tersebut sesuai dengan kata-kata kunci W [i]. Kolom ke-8 berisi kata W [i - Nk] dari kunci dengan angka berkurang W [43 - 4] = W [39], dan kolom ke-3 - kata kunci W [i - 1] = W [42], W sebelumnya [i] = W [43].
Arti kata W [39] dalam kolom ke-8 tidak diketahui dan kami menemukannya dari data awal menggunakan rumus:
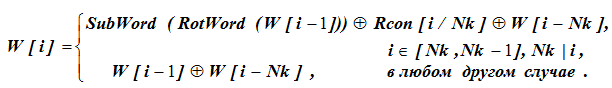
Untuk perhitungan rumus, kondisi untuk memilih garis rumus diperiksa terlebih dahulu. Untuk W [43], i = 43 dan Nk tidak sepenuhnya membagi nilai 43, yaitu, untuk i = 43 nilai W [i] ditentukan oleh garis bawah rumus: W [43] = W [42] W [39]. Di sini, untuk nilai W [42] dan W [43] yang diberikan, istilah W terakhir [39] tidak didefinisikan.
Kemudian W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.
Dalam mod2 aritmetika biner, operasi penjumlahan dan pengurangan adalah setara, oleh karena itu, perhitungan bitwise untuk masing-masing 4 byte kata kunci W [39] berbentuk (Tabel 5):
Tabel 5 - Perhitungan byte kata kunci W [39].

Dengan demikian, nilai kata kunci W [39] = 575c006e ditemukan. Kami mentransfer nilai ini ke kolom ke-3, ke baris i = 40 dan ke kolom ke-9 ke baris i = 39.
Perhitungan di baris i = 40 dilakukan seperti ketika memperluas kunci.
Kata yang tidak diketahui W [i - Nk] = W [40 –Nk] = W [i = 36] harus ditentukan seperti pada kasus sebelumnya dengan perbedaan W [36] = W [40] 7 kolom baris 40.
Pada gilirannya, nilai dalam 7- Kolom ke-4 dari baris 40 dibentuk sebagai jumlah (OR) dari kolom ke-5 dan ke-6. Nilai kolom 5 diperoleh dari W [39] setelah shift siklik RotWord (kolom 4) dan operasi penggantian SubWord (kolom 5).
Hasil dari tindakan ini berupa
RotWord (575c006e) = 5c006e57; SubWord (5c006e57) = 4a639f5b.
Nilai di kolom 6 diperoleh sebagai konstanta
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9 .
Konstanta ini diwakili oleh byte heksadesimal
2 9 ≈100000000 = x 9 , tetapi tidak ada byte seperti itu di bidang GF (2 8 ): perlu untuk menemukan sisa divisi dengan polinomial yang tidak dapat direduksi, mis.
Setelah memasukkan konstanta dalam kata kunci, kami memiliki
Rcon [j = 40 / Nk] = 36000000 (kolom ke-6). Nilai kolom 7 diperoleh sebagai (kolom 7) = (kolom 5) ⊕ (kolom 6) = 4a639f5b⊕36000000 = 7c639f5b.
Dan akhirnya, untuk
W [36] = W [40] (kolom ke-7 dari baris 40) = d014f9a8 7c639f5b = ac7766f3.
Perhitungan lebih lanjut dengan analogi mengarah pada hasil akhir - kunci sandi.
Ada informasi lebih lanjut tentang fungsi w dan RotWord, Rcon dan SubWord. Misalkan kita dilambangkan dengan Kr [j] - byte ke-j dari kunci putaran ke-r dan w [i] seperti dalam dokumentasi.
Kita mendapatkan: Kr = (w [Nk ∙ r], w [Nk ∙ r + 1], · · ·, w [Nk ∙ r + Nk - 1]).
Untuk i yang berbeda, kami memiliki relasi berikut
untuk i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr +1), w [i] = w [i - Nk] xor w [i - 1] dan
untuk i = 0 mod Nk, w [i] = w [i - Nk] xor SubWord (RotWord (w [i - 1])) xorRcon [i / Nk].
Karena itu, untuk i ≠ 0modNk, Nk 0≤i <Nb ∙ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] dan untuk i = 0modNk, w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk - 1])) xorRcon [i + Nk / Nk]
Dengan AES-256, Anda perlu menambahkan operasi Subword ketika saya sebanding dengan 4mod Nk. Jadi dimungkinkan untuk menyimpulkan kunci sebelumnya dari subkunci terakhir dan langkah demi langkah mendapatkan nilai K0 dari kunci sandi.
Fondasi matematika dari cipher AES - 128 cukup lengkap dan terperinci di sini .
Mari kita beralih ke pemetaan lapangan ℓ: GF (2 8 ) → GF (2 8 ); x → x 2 + x. Gambar peta ini
1 = Im (l) memiliki dimensi redup GF (2) (1) = 7.
Persamaan x2 + x = θ, di mana θ 1 memiliki dua solusi yang berbeda (akar persamaan) 1, 2є GF (2 8 ).
Dengan teorema Vieta, x1⊕x2 = 1, jumlah akar sama dengan koefisien persamaan pada x 2 dengan tanda yang berlawanan, dan produk dari akar x1⊗x2 = θ sama dengan istilah bebas persamaan (dalam persamaan kami dengan tanda yang berlawanan).
Diketahui bahwa dalam aritmatika bidang biner, operasi penambahan dan pengurangan elemen mod2 adalah setara.

Dengan demikian, akar persamaan terkait dengan rasio x2 = x1⊕1, karena koefisien pada x dalam persamaan adalah 1. Ini berarti bahwa dalam representasi desimal elemen-elemen bidang dengan urutan leksikografisnya, mereka ditempatkan satu demi satu, hanya berbeda satu per satu.
Jadi untuk x = 0 dan x = 1 dan untuk x = 2 dan x = 3 kita dapatkan:

Hasil (gambar) pemetaan dalam pasangan tereduksi (0, 1); (2, 3) sepenuhnya bertepatan, mis. dua jenis sesuai dengan satu gambar. Akibatnya, kardinalitas gambar adalah dua kali lebih kecil dari kardinalitas preimage dan dimensi elemen-elemennya adalah 7.
Produk pasangan akar, yaitu, istilah bebas dari persamaan kuadrat mudah ditentukan melalui representasi kekuatan elemen-elemen bidang (gambar terbalik). Dalam hal ini, eksponen diringkas mod255, yaitu modulo urutan kelompok multiplikasi GF bidang (2 8 ).