Saya ingat melihat foto di atas pada Flickr suatu hari dan mematahkan otak saya mencoba mencari tahu apa yang salah dengannya. Intinya adalah bahwa baling-baling berputar pada saat sensor gerak di kamera "membaca bacaan", yaitu, selama pemaparan kamera, ada beberapa gerakan. Ini sangat layak untuk dipikirkan, mari kita pikirkan bersama.
Banyak kamera digital saat ini menggunakan sensor CMOS sebagai perangkat "penginderaan", yang juga dikenal sebagai sensor piksel aktif., yang berfungsi dengan mengakumulasi muatan elektronik saat cahaya menerimanya. Setelah waktu tertentu - waktu pencahayaan - muatan ditransfer secara berurutan kembali ke kamera untuk diproses lebih lanjut. Kamera kemudian memindai gambar, menjaga baris piksel garis demi garis. Gambar akan terdistorsi jika ada gerakan selama pemotretan. Sebagai ilustrasi, bayangkan menembak baling-baling yang berputar. Dalam animasi di bawah ini, garis merah sesuai dengan posisi baca saat ini dan baling-baling terus berputar saat membaca. Bagian di bawah garis merah adalah gambar yang dihasilkan.
Baling-baling pertama menghasilkan 1/10 revolusi selama paparan:
Berlangganan ke saluran:
@Ontol - teks / video paling menarik sepanjang masa dan orang, yang memengaruhi gambar dunia
@META LEARNING - tempat saya membagikan temuan saya yang paling berguna tentang pendidikan dan peran TI / permainan dalam pendidikan (serta pemikiran Anton tentang topik ini) Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
Gambar sedikit terdistorsi, tetapi tidak ada yang kritis. Baling-baling sekarang akan bergerak 10 kali lebih cepat, membuat rotasi penuh selama paparan:
Ini sudah terlihat seperti gambar yang kami lihat di awal. Lima kali per eksposur:
Ini sudah terlalu banyak, sehingga Anda bisa keluar dari gulungan. Mari bersenang-senang dan periksa bagaimana objek yang berbeda akan melihat kecepatan rotasi berbeda per eksposur.
Baling-baling yang sama persis:
Baling baling besar:
Roda mobil:
Kita dapat melihat efek rana bergulir sebagai semacam transformasi koordinat objek nyata dari "ruang objek" ke "ruang gambar" objek yang terdistorsi. Animasi di bawah ini menunjukkan apa yang terjadi pada sistem koordinat Cartesian ketika jumlah revolusi meningkat. Pada kecepatan rendah, deformasi tidak signifikan - jumlahnya meningkat menjadi satu, dan setiap sisi sistem koordinat bergerak berurutan ke sisi kanan gambar. Ini adalah transformasi yang agak rumit untuk dipahami, tetapi mudah dipahami.
Biarkan gambar menjadi I (r, θ), objek nyata (berputar) akan menjadi f (r, θ), di mana (r, θ) adalah koordinat kutub 2D. Kami memilih koordinat kutub untuk tugas ini karena gerakan rotasi objek.
Objek berputar dengan frekuensi sudut ω, dan rana bergerak di sepanjang gambar dengan kecepatan v secara vertikal. Pada posisi (r, θ) dalam gambar, jarak yang telah dilalui rana sejak awal eksposur adalah y = rsinθ, di mana waktu berlalu sejak saat itu adalah (rsinθ) / v. Selama waktu ini, objek dirotasi oleh radian (ω / v) rsinθ). Jadi, kita mendapatkan
I (r, θ) = f (r, θ + (ω / v) rsinθ),
yang merupakan transformasi yang diperlukan. Rasio ω / v sebanding dengan jumlah rotasi per eksposur dan parameterisasi transformasi.
Untuk mendapatkan pemahaman yang lebih dalam tentang bentuk baling-baling yang jelas, kita dapat mempertimbangkan objek yang terdiri dari baling-baling P , di mana f bukan nol hanya untuk
θ = 2π / P, 4π / P… 2π = 2pπ / P untuk 1 <p <P.
Gambar I bukan nol untuk θ + (ω / v) rsinθ = 2pπ / P atau
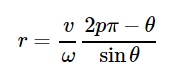
dalam sistem koordinat Cartesian, ia menjadi
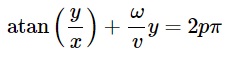
dan membantu kami dalam menjelaskan alasan mengapa baling-baling mengambil bentuk-S - ini hanyalah fungsi dari arctangent di ruang gambar. Keren. Di bawah ini saya merencanakan fungsi ini dengan satu set lima baling-baling baling-baling dengan offset awal yang sedikit berbeda, Anda dapat melihatnya di pemutaran. Mereka sangat mirip dengan bentuk dalam animasi di atas.
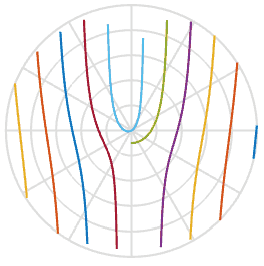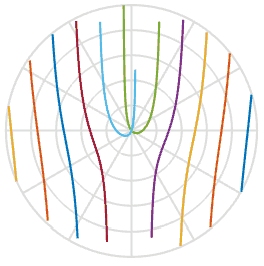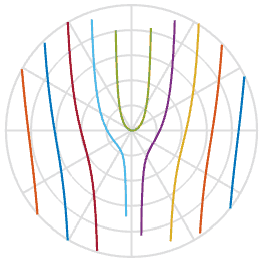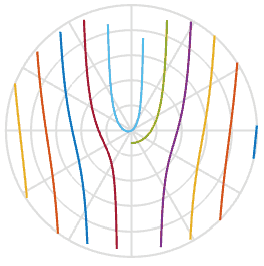
Karena kami belajar sedikit lebih banyak tentang prosesnya, dapatkah kami memperbaiki foto yang rusak? Dengan menggunakan salah satu gambar di atas, saya dapat menggambar garis melaluinya, memutar kembali dan memasukkan piksel tersebut ke gambar baru. Dalam animasi di bawah ini, saya memindai gambar di sebelah kiri, ditandai dengan garis merah, dan kemudian memutar piksel di sepanjang garis itu untuk mendapatkan gambar baru. Dengan cara ini kita dapat membuat ulang gambar objek nyata, bahkan jika rana bergulir yang mengganggu telah merusak foto Anda.
Eh, jika saya lebih baik di Photoshop, saya akan mengekstrak baling-baling dari foto asli di Flickr, mengeditnya dan memasukkannya kembali ke foto. Saya rasa saya tahu apa yang akan saya lakukan di masa depan.
Jika Anda ingin mengetahui jumlah sebenarnya bilah di foto di awal pos dan kecepatan rotasi, Anda dapat membaca pos yang luar biasa ini di Tumblr oleh Daniel Walsh , di mana ia memberikan penjelasan matematis.
Dia pikir kita bisa menghitung jumlah bilah dengan mengurangi bilah "bawah" dari yang "atas", jadi kita mendapatkan tiga bilah di gambar itu. Kita juga tahu bahwa baling-baling berputar sekitar dua kali selama paparan, jadi jika kita mencoba untuk "membatalkan" rotasi pada beberapa kecepatan yang berbeda, kita mendapatkan sesuatu seperti ini:
Saya harus mencari tahu di mana pusat baling-baling itu, jadi saya menggambar lingkaran. Rupanya, pusat harus berada di suatu tempat di dekatnya. Sayangnya, satu bilah hilang, tetapi ada cukup informasi untuk menampilkannya.
Saya menemukan tempat di mana semuanya bersinggungan paling banyak, jadi pada kecepatan rotasi ini (2.39 putaran per eksposur), seperti inilah tampilan gambar dan bilah asli:
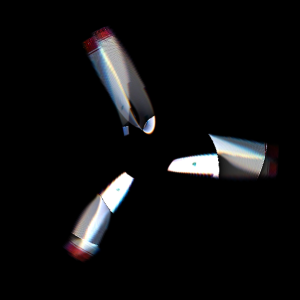
Sayangnya, gambarnya tidak sempurna, tetapi setidaknya sangat dekat dengan kenyataan.
Tentang penulis: Jason Cole adalah seorang mahasiswa pascasarjana dari London yang bersemangat tentang matematika, fisika dan visualisasi data. Inilah situs webnya . Dan artikel itu diterbitkan di sini .
Diskusi Berita Peretas
Menambahkan. video
Berlangganan ke saluran:
@Ontol - teks / video paling menarik sepanjang masa dan orang, yang memengaruhi gambar dunia
@META TRAINING , tempat saya membagikan temuan saya yang paling berguna tentang pendidikan dan peran TI / game dalam pendidikan (serta pemikiran Anton tentang topik ini) Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
Pelajari detail cara mendapatkan profesi yang dicari dari awal atau Tingkatkan keterampilan dan gaji dengan menyelesaikan kursus online berbayar SkillFactory:
- Kursus Pembelajaran Mesin (12 minggu)
- Belajar Ilmu Data dari awal (12 bulan)
- Profesi analis dengan level awal apa pun (9 bulan)
- Python untuk Kursus Pengembangan Web (9 bulan)