Heap Bottom Sort

Ini adalah artikel terakhir dalam seri tentang penyortiran tumpukan. Dalam kuliah sebelumnya, kami melihat berbagai macam struktur tumpukan yang menunjukkan hasil kecepatan yang sangat baik. Timbul pertanyaan: tumpukan apa yang paling efektif dalam hal penyortiran? Jawabannya adalah: yang akan kita lihat hari ini.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

Tumpukan mewah yang kami lihat sebelumnya baik-baik saja, tetapi tumpukan paling efisien adalah tumpukan standar dengan peningkatan kliring.



Apa itu kliring, mengapa dibutuhkan dalam tumpukan dan cara kerjanya dijelaskan di bagian pertama dari serangkaian artikel.



Penyaringan standar dalam penyortiran klasik oleh sekelompok bekerja kira-kira "dahi" - elemen dari akar subtree dikirim ke clipboard, elemen dari cabang, menurut hasil perbandingan, naik. Ini cukup sederhana, tetapi ada terlalu banyak perbandingan.







Di jalur menanjak, perbandingan diselamatkan karena fakta bahwa orang tua hampir tidak dibandingkan dengan keturunan mereka, pada dasarnya, hanya keturunan yang dibandingkan satu sama lain. Dalam heapsort biasa, kedua orang tua dibandingkan dengan anak-anak dan anak-anak dibandingkan satu sama lain - oleh karena itu, ada hampir satu setengah kali lebih banyak perbandingan dengan jumlah pertukaran yang sama.



Jadi bagaimana cara kerjanya, mari kita lihat contoh spesifik. Misalkan kita memiliki sebuah array di mana tumpukan hampir terbentuk - yang tersisa adalah menyaring root. Untuk semua node lain, kondisi terpenuhi - keturunan apa pun tidak lebih dari induknya.



Pertama-tama, dari titik di mana penyaringan dilakukan, Anda harus turun, bersama keturunan besar. Tumpukannya adalah biner - yaitu, kami memiliki anak kiri dan anak kanan. Kami pergi ke cabang di mana keturunan lebih besar. Pada tahap ini, jumlah utama perbandingan terjadi - anak-anak kiri / kanan dibandingkan satu sama lain.







Setelah mencapai daun di tingkat terakhir, kami memutuskan cabang, nilai-nilai yang perlu digeser ke atas. Tetapi Anda tidak perlu memindahkan seluruh cabang, tetapi hanya bagian yang lebih besar dari akar dari mana Anda memulai.



Oleh karena itu, kita naik cabang ke simpul terdekat, yang lebih besar dari root.







Langkah terakhir - menggunakan variabel buffer, kami menggeser nilai-nilai node ke cabang.







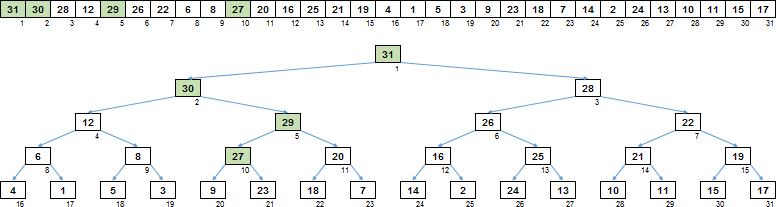
Itu dia. Ayakan ascenden membentuk pohon penyortiran dari array, di mana setiap orang tua lebih besar dari turunannya.



Animasi terakhir:

Implementasi Python 3.7

Algoritma pemilahan dasar tidak berbeda dari heapsort biasa:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

Turun ke lembar bawah nyaman / secara visual dimasukkan ke dalam fungsi yang terpisah:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

Dan yang paling penting - pembukaan, pertama turun, kemudian muncul ke atas:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

Murni secara empiris - menurut pengukuran saya, jenis tumpukan naik adalah 1,5 kali lebih cepat dari jenis tumpukan biasa.



Menurut beberapa informasi (pada halaman algoritma di Wikipedia, dalam PDF di bagian "Tautan"), BottomUp HeapSort rata-rata mengungguli bahkan penyortiran cepat - untuk array yang cukup besar dengan ukuran lebih dari 16 ribu elemen.

Tautan

Bottom-up heapsort



Varian dari Heapsort dengan Jumlah Perbandingan yang Hampir Optimal



Membangun Heapsort Cepat



Varian baru dari heapsort mengalahkan, secara rata-rata, quicksort (jika n tidak terlalu kecil)

Artikel Seri:

• Aplikasi Excel AlgoLab.xlsm
• Pertukaran sortir
• Sisipkan sisipan
• Sortir berdasarkan pilihan
  • Jenis tumpukan: piramida n-ary
  • Heap Sorts: Leonardo Numbers
  • Heap Sorts: Weap Heap
  • Jenis tumpukan: pohon Cartesian
  • Heap Sorts: Tournament Tree
  • Heap sorting: kliring naik
• Gabungkan Urusan
• Urutkan berdasarkan Distribusi
• Jenis hibrida

Penyortiran hari ini telah ditambahkan ke aplikasi AlgoLab, yang menggunakannya - perbarui file excel dengan makro.