🤳🏻 😀 👼 Prinsip pengoperasian RSLOS 🔱 💯 🏠

pengantar

Linear Feedback Shift Register (LFSR) adalah register geser dari kata-kata bit, di mana nilai bit input diatur secara unik oleh beberapa fungsi berdasarkan nilai bit register yang tersisa sebelum pergeseran. Register geser dapat berupa rangkaian listrik yang terdiri dari komponen diskrit: transistor, resistor, juga dapat diintegrasikan ke dalam rangkaian mikro atau diimplementasikan dalam suatu program. Penambahan umpan balik mengubah register geser menjadi generator bilangan acak semu, yang banyak digunakan dalam kriptografi. Pada artikel ini, kami akan menganalisis prinsip pengoperasian RSLOS dari perangkat keras hingga berbagai aplikasinya.

Register, secara umum, adalah rangkaian yang terdiri dari elemen memori satu-bit yang saling berhubungan. Sirkuit semacam itu dapat menulis, menyimpan, membaca data biner n-bit. Artikel ini membahas jenis register yang disebut register geser. Paling sering, register geser dirakit berdasarkan D-flip-flop yang terhubung seri, dan jumlah flip-flop ini sama dengan jumlah bit n. Kami memulai artikel ini dengan prinsip-prinsip pemicu-D.

D-trigger

Mari kita secara singkat menyentuh dasar-dasarnya. Secara global, elektronik dapat dibagi menjadi dua bagian: analog dan digital. Fitur utama yang kedua adalah bahwa sinyal diatur oleh level tegangan diskrit. Selain itu, hanya ada dua level terpisah. Jadi, alih-alih mencatat voltase dalam volt, cukup menyebutkan salah satu dari dua level diskrit. Beginilah nama "nol" dan "satu" muncul. Faktanya, mereka menentukan beberapa level tegangan, yang bisa berupa apa saja. Meskipun, dalam banyak kasus, "nol" berarti tingkat 0 volt, dan "satu" adalah tingkat 5 V, 3,3 V, 1,8 V, 1,5 V, dll. Jadi, frase "pada masukan nol, pada keluaran satu" berarti: "pada tegangan masukan yang sesuai dengan tingkat nol, pada tegangan keluaran yang sesuai dengan tingkat satu."

. , ? D- , ! .

– , .

D- – , . ,

D- , . : D (), C ( , , , clk, clock) Q (). : , , . , , .

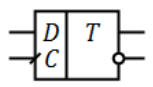
. 1 - D-

D- : C, . . . - «», «», «».


(D)	(Q)	(D)	(Q)
0	0	0	0
0	1	0	0
1	0	1	1
1	1	1	1

« ». , ( ) . , . , .. . , , . , .

, . D- . , . , , . D-, .

, n D-. . , , . .

? , , , . . «» . , , . ? ( ). . . , , , . . . , , . , : .

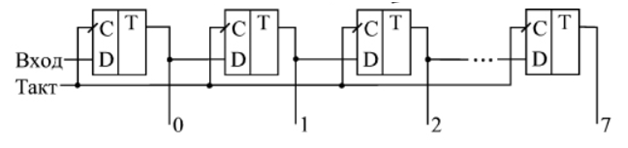
№		0	1	2	3
0	1	0	0	0	0
1	0	1	0	0	0
2	0	0	1	0	0
3	0	0	0	1	0
4	0	0	0	0	1
5	0	0	0	0	0

- . . ? , . . , , , , . .

$\ sum_ {i = 1} ^ n h_i x_i (mod 2)$

h_i- , . .

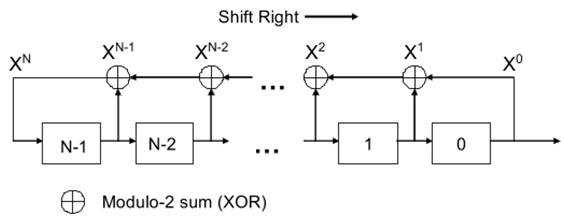
? . , , . , , 1 , . . . , .

, . ? , , . n , n . , . X_i. , . . . N, X_i+N = X_i i. 2ⁿ-1, -. , , 2ⁿ-1. .

$(x) = a_n x ^ n + a_ {n-1} x ^ {n-1} + \ titik + a_1 x + 1$

GF(2). . t + 1, (x) p:

Y(t) t. T – n :

$T = \ kiri (\ begin {array} {ccccc} a_1 & a_2 & \ ldots & a_ {n-1} & a_n \\ 1 & 0 & \ ldots & 0 & 0 \\ 0 & 1 & \ ldots & 0 & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & 0 & \ ldots & 1 & 0 \ \ end {larik} \ kanan)$

, , . , GF(2) - : k 2^k-1. . , . , . .

n	LFSR-2	LFSR-4
2	2, 1
3	3, 2
4	4, 3
5	5, 3	5, 4, 3, 2
6	6, 5	6, 5, 3, 2
7	7, 6	7, 6, 5, 4
8		8, 6, 5, 4

, , . , n= 8 :

. : . . , . , , , . . : .

. . . . 2ⁿ¹, 2ⁿ², . ., 2^n1+n2+… , n1, n2, … .

. . . — 2017. — 117 .
. . . — , 2008. — 314 .
Eastlake D., Schiller J., Crocker S. Randomness requirements for security. — 2005. — 48 .

Prinsip pengoperasian RSLOS

pengantar

D-trigger

More articles: