Clever Geek Handbook

Fungsi hash berdasarkan automata seluler

Fungsi hash adalah fungsi yang mengubah sekumpulan data input dengan panjang acak menjadi urutan bit dengan panjang tetap. Fungsi hash memainkan peran penting dalam kriptografi modern. Kemajuan teknologi, persyaratan baru untuk keamanan, dan kompleksitas komputasi muncul. Keluarga algoritme SHA tetap menjadi pemimpin di antara algoritme hashing di banyak area, tetapi ada keluarga algoritme lain yang didasarkan pada automata seluler yang layak mendapatkan perhatian semua orang.





Automata seluler

Otomat seluler adalah hal yang cukup umum yang layak mendapat pos terpisah . Namun, singkatnya, ini adalah model diskrit, yang merupakan kisi dengan dimensi yang berubah-ubah, setiap sel yang setiap saat dapat mengambil salah satu dari sekumpulan keadaan terbatas, dan aturan untuk transisi sel dari satu keadaan ke keadaan lain ditentukan.





Dalam kasus automata seluler dasar, kisi-kisi sel memiliki dimensi satu dimensi.





Dalam robot seluler, untuk setiap sel, ada satu set sel lain, yang disebut lingkungan, yang menentukan keadaan sel selanjutnya. Keadaan awal adalah keadaan di mana nilai sel dan lingkungannya ditentukan pada waktu t. Sekarang generasi sel baru dibuat saat "t" bertambah 1.





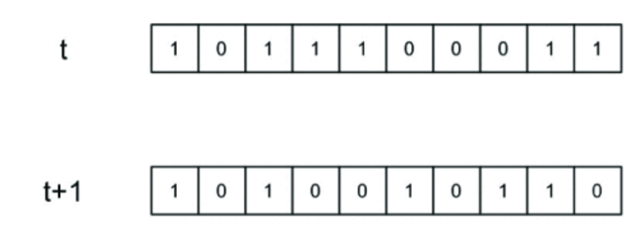
30, :





C ^ {t + 1} _s = C ^ t_ {s-1} \ XOR \ (C ^ t_s \ OR \ C ^ t_ {s + 1})

:





  • , .





  • ( ).





  • .





.









?

c k, : 128, 192 256 .





  1. c :





    size (c) \ text {mod} 512 = 0 \ text {and} size (c)> = 512





    .





    C.





  2. k.





    size (k) \ text {mod} 512 = 0 \ text {and} size (k)> = 512





    k





  3. C 512 .





  4. 512 , 8 64 .





  5. 512 30.





  6. 5 512 ().





  7.   XOR 5 512 .





  8.   , 1.





  9.   6, 7 8 , 512 , .





, .





, .





64 .





  1. a = e





    , e Sebuah





  2. b = J (g, h, K_1) b = J (g, h, K_5)





    , a = J (g, h, K_1) a = J (g, h, K_5)





    J (x, y, z) = ((\ text {ROTL} ^ {47} (x) \ text {XOR} \, Aturan \, 30 (\ text {ROTL} ^ {37} (y ')) \ teks {AND} ((\ text {ROTR} ^ {17} (z)))





  3. c = G (e, f, K_2) c = G (e, f, K_6)





      , c = G (e, f, K_2) c = G (e, f, K_6)





    G (x, y, z) = (Aturan134 (Aturan30 (x ')) \ teks {OR} y) \ teks {XOR} (Aturan30 (z') \ teks {AND} x)





  4. d = F (a, c)





    F (x, y) = Aturan30 (x) \ teks {XOR} y '





  5. e = J (a, d, K_4) e = J (a, d, K_8)





      , e = J (a, d, K_4) e = J (a, d, K_8)





      J 1.





  6. f = H (b, d)





    H (x, y) = \ text {ROTL} ^ {17} (x) \ text {XOR} \ text {ROTL} ^ {59} (y)





  7. g = I (c, f)





    I (x, y) = \ text {ROTL} ^ {41} (x ') \ text {XOR} \ text {Rule134} (\ text {Rule30} (\ text {ROTL} ^ {31} (y') ))





  8. h = H (a, K_3) h = H (a, K_7)





      , h = H (a, K_3) h = H (c, K_7)





      H. 4.





ROTL — , ROTR — .





. :





putaran = '1' (512 ) + '0' (512 ) mod 512 .





30 , - . . , .





:







More articles:


All Articles