🤳🏼 🏒 🙎🏾 Batasan daya representatif dan estimasi kesalahan generalisasi untuk jaringan saraf grafis 💲 🧛🏾 😅

Saat ini, salah satu tren dalam studi jaringan syaraf tiruan grafik adalah analisis pengoperasian arsitektur tersebut, perbandingan dengan metode nuklir, penilaian kompleksitas dan kemampuan generalisasi. Semua ini membantu untuk memahami titik lemah dari model yang ada dan menciptakan ruang untuk model baru.

Pekerjaan ini bertujuan untuk menyelidiki dua masalah yang berkaitan dengan jaringan saraf grafik. Pertama, penulis memberikan contoh grafik yang berbeda strukturnya, tetapi tidak dapat dibedakan untuk GNN yang sederhana dan yang lebih kuat . Kedua, mereka mengikat kesalahan generalisasi untuk grafik jaringan saraf lebih akurat daripada batas VC.

pengantar

Jaringan neural grafik adalah model yang bekerja langsung dengan grafik. Mereka memungkinkan Anda untuk memperhitungkan informasi tentang struktur. GNN tipikal menyertakan sejumlah kecil lapisan yang diterapkan secara berurutan, memperbarui representasi simpul di setiap iterasi. Contoh arsitektur populer: GCN , GraphSAGE , GAT , GIN .

Proses memperbarui embeddings vertex untuk arsitektur GNN apa pun dapat diringkas dengan dua rumus:

$a_v ^ {t + 1} = AGG \ kiri (h_w ^ t: w \ in \ mathcal {N} \ left (v \ right) \ right) \\ h_v ^ {t + 1} = GABUNGKAN \ kiri (h_v ^ t, a_v ^ {t + 1} \ kanan),$

dimana AGG biasanya merupakan fungsi yang tidak berubah terhadap permutasi ( jumlah , rata-rata , maks , dll.), GABUNGKAN adalah fungsi yang menggabungkan representasi simpul dan tetangganya.

Pohon komputasi untuk GNN dua lapis menggunakan contoh node A. Sumber: https://eng.uber.com/uber-eats-graph-learning/

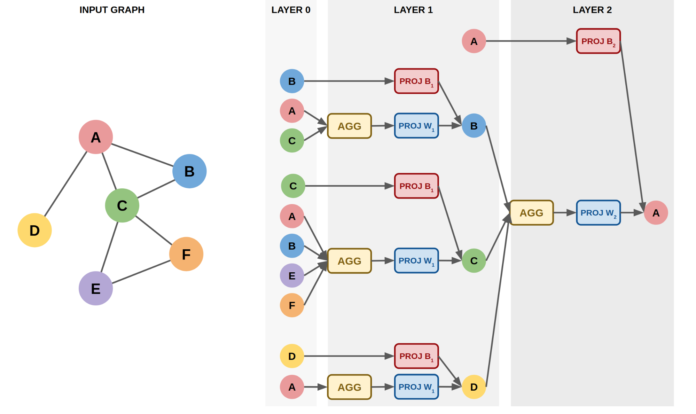
Arsitektur yang lebih maju dapat mempertimbangkan informasi tambahan seperti fitur tepi, sudut tepi, dll.

Artikel ini membahas kelas GNN untuk masalah klasifikasi grafik. Model ini disusun seperti ini:

Pertama, simpul adalah embeddings menggunakan langkah-langkah L dari konvolusi graf
(, sum, mean, max)

GNN:

(LU-GNN). GCN, GraphSAGE, GAT, GIN
CPNGNN, , 1 d, d - ( port numbering)
DimeNet, 3D-,

LU-GNN

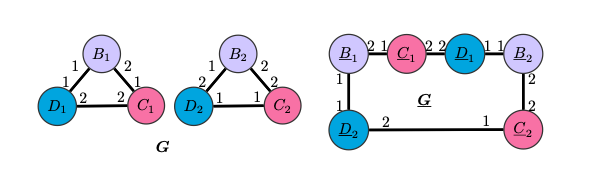
G G LU-GNN, , , readout-, . CPNGNN G G, .

CPNGNN

, “” , CPNGNN .

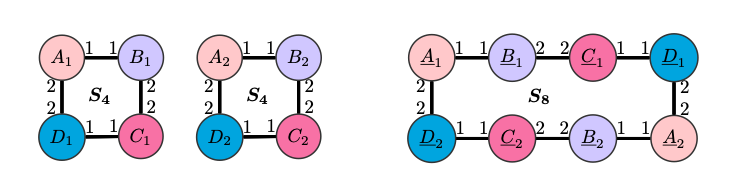
S₈ S₄ , , ( ), , , CPNGNN readout-, , . , .

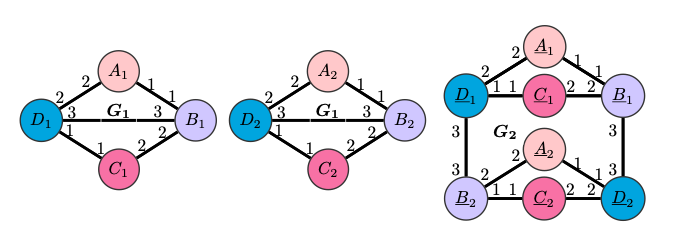
CPNGNN G₂ G₁. , DimeNet , , , , $\ angle A_1B_1C_1$ $\angle \underline{A}_1\underline{B}_1\underline{C}_1$ .

DimeNet

DimeNet G₄ , G₃, . , . , G₄ G₃ S₄ S₈, , , DimeNet S₄ S₈ .

GNN

. , , .

GNN, :

DimeNet
message- $m_{uv}^{\left(l\right)}$ $\Phi_{uv}$ $\underline{m}_{uv}^{\left(l\right)} = \underline{f}\left(m_{uv}^{\left(l\right)}, \Phi_{uv}\right)$
$\left(c_v\left(i\right), t_{i, v}\right)$ , c - i- v, t - .

:

$h_{v}^{\left( l + 1 \right)} = f \left( h_{v}^{\left( l \right)}, \underline{m}_{c_v\left( 1 \right)v}^{\left( l \right )}, t_{1, v}, ..., \underline{m}_{c_v\left( d \left( v \right ) \right)v}^{\left( l \right )}, t_{ d \left( v \right ), v} \right )$
readout-

: LU-GNN,

$h_v^{l + 1} = \phi \left( W_1x_v + W_2 \rho \left( \sum_{u \in \mathcal{N} \left( v \right)} g\left( h_u^l \right)\right) \right),$

$\phi,\ g,\ \rho$ - , x_v - v, , $\rho \left(0\right) = 0,\ \forall v: \lVert x_v \rVert_2 \le B_x,\ \forall x \in \mathbb{R}^r: \lVert \phi \left( x \right ) \rVert_{\infty} \le b < \infty,\ \phi\left( 0 \right ) = 0,\ g\left( 0 \right ) = 0$ . , $\phi,\ g,\ \rho$ $C_{\phi},\ C_{g},\ C_{\rho}$ , $\lVert W_1 \rVert_2 \le B_1,\ \lVert W_2 \rVert_2 \le B_2$ . $W_1,\ W_2,\ \phi,\ g,\ \rho$ GNN.

. $\beta$ $\lVert \beta \rVert_2 \le B_{\beta}$ .

$f\left(G\right)$ - GNN $y \in \{0, 1\}$ , $p\left( f \left( G \right ), y \right ) = y \left( 2f \left( G \right ) - 1 \right ) + \left( 1 - y \right ) \left( 1 - 2 f \left( G \right ) \right )$ - , $p\left( f \left( G \right ), y \right ) < 0$ .

, $a = -p\left( f \left( G \right ), y \right )$ , $\mathbb{I}\left[\right]$ - :

$loss_{\gamma}\left( a \right ) = \mathbb{I}\left[ a > 0\right ] + (1 + \frac{a}{\gamma})\mathbb{I}\left[ a \in \left[ \gamma, 0 \right ] \right].$

GNN $\{G_j, y_j\}_{j=1}^m$ :

$\hat{\mathcal{R}}\left( f \right) = \frac{1}{m} \sum_{j = 1}^m loss_{\gamma} \left( -p\left( f \left(G_j\right), y_j \right) \right)$

, , , , GNN . , (GNN, ), , , .

, :

RNN

$\mathcal{C}$ - “ ”: $\mathcal{C} = C_{\phi}C_gC_{\rho}B_2$ , r - , d - , m - , L - , $\gamma$ - ,

, , $\ tilde {\ mathcal {O}} \ kiri (r ^ 3N / \ sqrt {m} \ kanan)$

GNN, ( readout-), . , , .

( ), . , , , , , , .

Bukti dan informasi lebih rinci dapat ditemukan dengan membaca artikel asli atau dengan melihat laporan dari salah satu penulis.

Batasan daya representatif dan estimasi kesalahan generalisasi untuk jaringan saraf grafis

pengantar

LU-GNN

CPNGNN

DimeNet

GNN

More articles: