Saat mempelajari kursus Algoritma pada String , saya menghadapi masalah dalam membuat pohon sufiks . Mengikuti tautan untuk materi tambahan, saya menemukan rekomendasi untuk "melihat komentar hebat ini di Stack Overflow ". Setelah mempelajari dan mengimplementasikan algoritma Ukkonen sesuai dengan deskripsi gratis yang diberikan , saya memutuskan untuk membagikan terjemahannya.
Di bawah ini adalah upaya untuk mendeskripsikan algoritma Ukkonen; pertama menunjukkan cara kerjanya pada string sederhana (yaitu string tidak berisi karakter duplikat), secara bertahap berkembang ke algoritme lengkap.
Beberapa pernyataan awal:
Apa yang kita bangun pada dasarnya adalah pohon awalan . Ini adalah simpul akar, yang ujung-ujungnya keluar dari simpul itu ke simpul baru, dan ujung-ujungnya keluar darinya, dan seterusnya.
Tetapi , tidak seperti pohon prefiks, label tepi bukanlah karakter tunggal, untuk setiap tepi label adalah sepasang angka [dari, ke] - penunjuk ke posisi dalam teks. Dalam hal ini, setiap tepi berisi string dengan panjang sembarang, tetapi hanya membutuhkan O (1) memori (dua penunjuk)
Prinsip dasar
Pertama, penulis ingin mendemonstrasikan cara membuat pohon sufiks dari string yang sangat sederhana, string tanpa karakter duplikat:
abc
Algoritme bekerja dalam beberapa langkah, dari kiri ke kanan . Satu langkah per karakter baris . Setiap langkah mungkin melibatkan lebih dari satu operasi individu, tetapi kita akan melihat (lihat pengamatan akhir di akhir) bahwa jumlah total operasi adalah O (n).
a
, [0, #]
- 0 . #
, , 1 ( a
).
, :
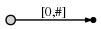
:

2 ( b
). : . :
a
-ab
b
:
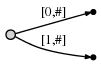
:
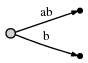
:
ab
, :[0, #]
. ,#
1 2.
O(1) , , , .
c
c
.
:
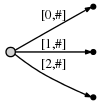
:
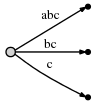
:
,
O(n),
#
, O(1). n, O(n)
:
, , . :
abcabxabcd
abc
, , ab
x
, abc
d
.
1 3: 3 :
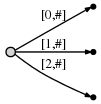
4: #
4. :

a
.
, ( #
), , , , :
(_, _, _)
,
, :
abc
(, '\0x', 0)
, .._
,_
'0\x',_
. , , , .
1 . , , , 1 ( )
. a
, a
, : abca
. :
[3, #]
. ,a
. , - . , .
(, 'a', 1)
. , -a
, , 1 . ,a
. , ( , , ).
, 2
Spoiler
[4, #]
, , a
3
: , , , (
). , ( a
). , ( , O(1)), .
5: #
5. :
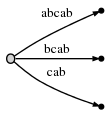
,
2, : ab
b
. - , :
a
. , ,
ab
.
b
.
, ( a
, abcab
), b
. : , b
.
, . :
(, 'a', 2)
( , ,b
)
3, , .
: ab
b
, ab
, b
. ? , ab
, ( b
) . , , , - , .
6, #
. :
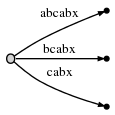
3, abx
, bx
x
. , ab
, x
. , x
, abcabx
:

- , O(1).
, abx
2. bx
. , . , , 1, , _
( 3 ).
1, :
-
_
-
_
, , ..b
-
_
1
C, (, 'b', 1)
, bcabx
, 1 , b
. O(1) , x
. , . x
, , :
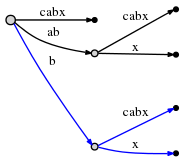
O(1),
1, (, 'x', 0)
, 1.
-. 2:
, , , , .
Spoiler
1 2
, , , , .
, . ( ):

, x
. _
0, . x
, :
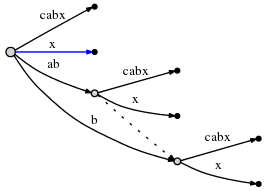
Spoiler
, .
7, #
= 7, , , a
. () , . , , (, 'a', 1)
.
Spoiler
#
, , #
8, #
= 8, b
, , , , (, 'a', 2)
, , b
. ( O(1)), . (1, '\0x', 0)
. 1
, ab
.
, #
= 9 'c', :
:
, #
c
, , , 'c'. , 'c' , (1, 'c', 1)
,
.
#
= 10
4, abcd
( 3 ), d
.
d
O(1):

_
, , .
3
_
, , , ,_
, . ,_
._
_
.
(2, 'c', 1)
, 2 :
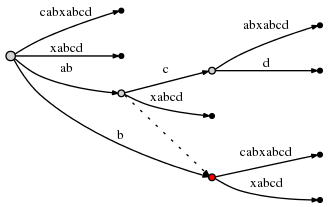
abcd
,
3 : bcd
. 3 , bcd
, d
.
, - 2 :
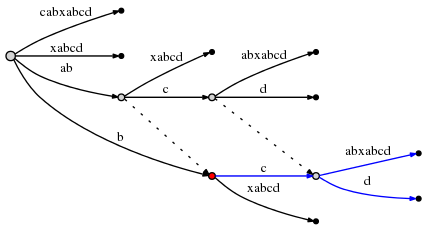
: , O(1). , , ab
b
( ), abc
bc
.
.
2, 3, . _
( ) , . (, 'c', 1)
.
, , c
: cabxabcd
, , c
. :
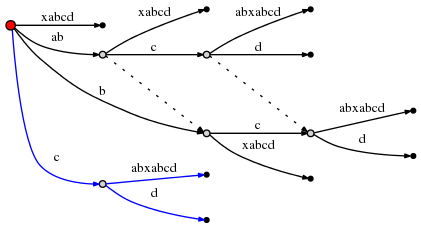
, 2 :
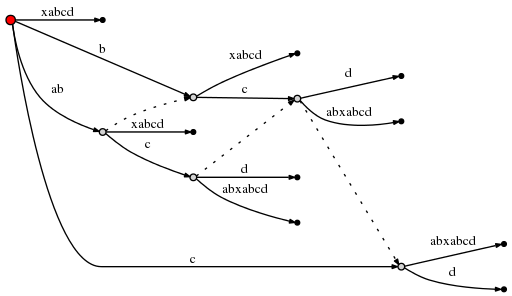
( Graphviz Dot . , , , , - )
1, _
, 1 (root, 'd', 0)
. , d
:
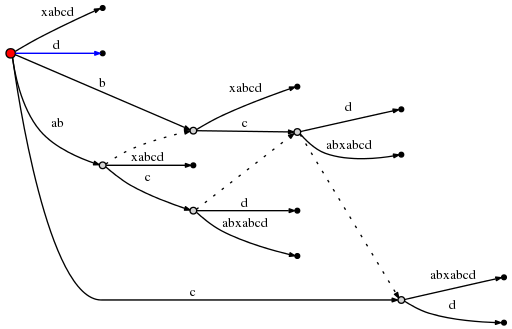
Spoiler
, . :
#
1 . O(1).
:
,
.
, . , #
. . : O(1), , , . ? ( , ).
, , , , ,
> 0. , , . , . ,
> 0, , .
Spoiler
,
> 0? , - , - . , . $
. ? → , , . , , .
- , , , . , , , .
? n , , n ( n + 1, ). ( ),
, O(1) .
, , , , , -, n ( n + 1). , O(n).
, : , , , , _
_
. , :
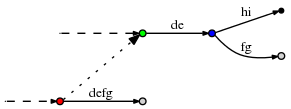
( . )
, (, 'd', 3)
, f
defg
. , , 3. (, 'd', 3)
. d
-, - de
, 2 . , , , (, 'f', 1)
.
_
,
, n. , , , , , n . , O(n2),
O(n), - _
O(n)?
. , (, , ), , , _
. , , , _
, , , , _
. _
,
,
O(n) , , -
O(n), O(n).
Catatan Penerjemah
Secara umum, algoritma dijelaskan dalam bahasa yang mudah dan dimengerti. Mengikuti uraiannya, dimungkinkan untuk menerapkannya, dan pengoptimalan alami akan terjadi dengan cepat. Saya menyoroti tempat-tempat yang membuat saya kesulitan dengan spoiler.
Dalam implementasi saya , alfabet ACGT digunakan, karena alfabet ini mengejar tujuan untuk lulus tes suatu masalah dalam suatu kursus.