
Saya telah berpartisipasi dalam latihan dengan Matriks Risiko Perusahaan.
Aksi berlangsung dalam tiga tahap. Yang pertama: anak laki-laki dan perempuan yang disurvei dengan pertanyaan seperti "apakah kamu sudah berhenti minum cognac di pagi hari", yang mana kamu hanya perlu menjawab "ya" atau "tidak".
Pada tahap kedua, matriks risiko "berbasis sains" ditampilkan.
Pada tahap permanen ketiga, semua divisi dari perusahaan itu mencoba dari tahun ke tahun untuk pindah ke posisi yang lebih rendah di matriks, tetapi ini hanya mungkin karena daya tarik pribadi. Mereka yang tidak bisa bergerak menjadi ekstrim pada setiap kegagalan bisnis.
1. Matriks risiko: lebih mudah untuk diisi, tidak nyaman untuk bekerja.
Berikut adalah Matriks Risiko khas yang ditawarkan Google.

Misalnya, Matriks Risiko acak dari laporan yang sangat lama ditemukan di Internet.
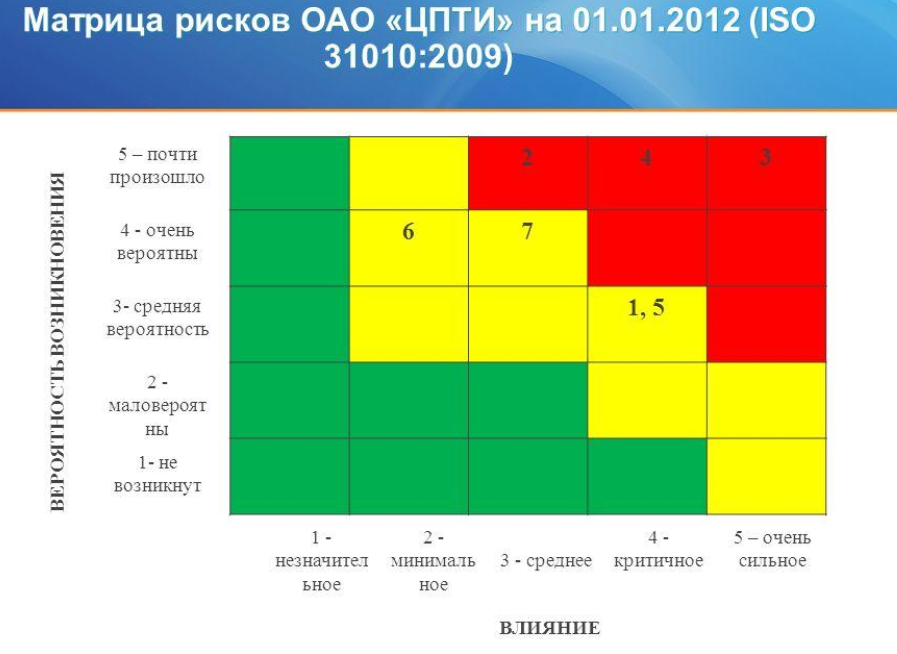
Angka-angka di dalam persegi panjang berwarna mewakili interpretasi risiko yang bermakna yang belum terlalu dibutuhkan. Deskripsi risiko sangat luas dan tidak jelas. Sulit dipercaya bahwa semua komponen deskripsi secara terpisah dan bersama-sama memberikan satu nomor dalam kisaran yang sangat sempit.
Jika Anda mengikuti matriks Google biasa, maka semua deskripsi yang bermakna tentang "probabilitas" dan "dampak" dapat dikaitkan dengan angka tertentu.
Berikut adalah template matriks Google yang dimodernisasi dengan probabilitas yang dikalikan sesuai dengan penskalaan horizontal dan vertikal.

Sangat tidak nyaman untuk menerapkan operasi matriks standar, karena ia simetris sehubungan dengan tambahan, bukan utama, diagonal.
Ada kemungkinan bahwa Matriks Risiko dalam formulir ini lebih nyaman bagi manajer. Penataan ulang dengan simetri diagonal utama tidak mengubah esensi matriks. Atau, Anda selalu dapat mundur dan kembali ke tampilan asli.
Matriks tersebut dibangun kembali dengan mengganti urutan baris dengan yang berlawanan (kesimetrisan terhadap sumbu tengah vertikal). Hasilnya, diperoleh matriks yang simetris terhadap diagonal utama.

Transformasi yang sama untuk Matriks Risiko yang dipelajari.

Angka selain 0 adalah angka risiko yang terkait dengan unit struktural tertentu. Pengkodean ini hanya terjadi sehubungan dengan hierarki birokrasi di perusahaan, dan bukan dengan risikonya. Misalnya, untuk elemen {1,5}. Dalam hal risiko, situasinya tidak berbeda jika deskripsi risiko1 dan risiko5 digabungkan. Jika ini adalah risiko yang berbeda, maka Anda dapat mengurangi langkah matriks dan menempatkan risiko pada posisi yang lebih tepat.
Pada akhirnya, transformasi harus menjadikan setiap risiko yang berbeda sebagai elemen yang terpisah.
Posisi [1,3] dalam sistem penomoran matriks standar berarti elemen di persimpangan baris ke-1 dan kolom ke-3. Untuk matriks yang dipertimbangkan, pada posisi [1,3] terdapat angka 2. Artinya jika ada skala dengan nilai maksimal “5 - hampir terjadi” (1.), maka pada [1,3] kita mengharapkan “3 - rata-rata” ( 0.6) pengaruh. Biarkan "pengaruh" dalam interval skala sesuai dengan kerusakan tertentu: 5-d5, 4-d4, 3-d3, 2-d2,1-d1. Kemudian jika dalam kurun waktu tertentu terdapat 1 kecelakaan dari kelompok 2, maka kerusakannya menjadi 1. * 0.6 * d3 * 1, dan jika n kecelakaan dari kelompok 2 terjadi pada periode yang sama maka kerusakannya adalah 1. * 0.6 * d3 * n
Kemudian matriks yang diselidiki akan berbentuk.

Transformasi lain dilakukan: transposisi dengan mengubah posisi kolom dan baris.

Baris terbawah legenda menjadi mubazir, karena probabilitas terkait diperhitungkan dalam nilai matriks. Kolom vertikal pertama juga diperhitungkan dalam nilai matriks, tetapi ini penting karena mengatur struktur peristiwa yang dapat direkam atau diprediksi selama periode tertentu. Memiliki vektor kolom dari jumlah kejadian yang terkait dengan jenis yang sesuai (sangat kuat, kritis, ...), Anda dapat mengalikan matriks dengan vektor kolom dengan cara standar dan mendapatkan jumlah kerusakan terstruktur.
Tanpa legenda, matriks akan terlihat seperti ini.

2. Matriks risiko: lebih mudah untuk menghitung, tidak nyaman untuk dianalisis.
Tugas utama pertama.
Setelah menerima matriks A, seseorang dapat melanjutkan untuk menyelesaikan masalah utama pertama: dengan jumlah dan kualitas peristiwa yang diketahui, hitung jumlah kerusakan.
Misalkan untuk periode tertentu terjadi 2 peristiwa "sangat kuat", 3 "kritis", 1 "rata-rata", 5 "minimal" dan 7 "tidak signifikan". Mengalikan matriks A dengan vektor jumlah kejadian, kita mendapatkan struktur kerusakan.

Kerusakan umum.

Sekarang Anda dapat memeriksa keakuratan perkiraan, membuat penyesuaian, mengevaluasi opsi yang memungkinkan untuk mengurangi jumlah kerusakan.
Transformasi matriks asli di atas dilakukan untuk mendapatkan prosedur kerusakan komputasi yang sederhana. Dari matriks A, Anda selalu dapat mengembalikan secara pasti ke matriks asli.
3. Matriks risiko: teori apa yang ada di baliknya?
Untuk matriks kuadrat non-degenerasi, ada transformasi linier satu-ke-satu yang sesuai dengan matriks ini. Saat melihat matriks, sulit untuk memahami transformasi linier mana yang berada di belakangnya. Selain itu, tidak diketahui dari dasar apa representasi matriks tersebut dihasilkan.
Matriks risiko adalah matriks persegi dan harus sesuai dengan beberapa jenis transformasi linier. Fakta ini tidak bergantung pada metode memperoleh matriks dan gagasan yang diterapkan dalam metode tertentu untuk memperoleh matriks.
Penting bahwa determinan dari matriks tersebut tidak nol. Ini adalah persyaratan metode yang memberikan representasi kanonik dari sebuah matriks.
Lebih lanjut, ditunjukkan bahwa ini bukan hanya batasan metode, tetapi persyaratan yang memenuhi kebutuhan praktik.
Matriks Risiko yang dianggap memiliki dua baris nol dan satu kolom nol. Bagaimanapun, determinan dari matriks ini akan sama dengan nol. Di bawah ini adalah grafik yang menunjukkan bagaimana perusahaan bermaksud untuk memitigasi risiko.

Tanda panah menunjukkan bagaimana risiko akan dikurangi. Tidak peduli bagaimana itu, penting bahwa dalam kasus ini situasi baru direpresentasikan lagi sebagai matriks. Matriks ini sesuai dengan beberapa jenis transformasi linier. Transisi dari matriks "lama" ke matriks "baru" adalah matriks dan transformasi linier.
Apa arti determinan bukan nol? Ini adalah kemampuan untuk berjalan maju mundur. Jika determinannya nol, maka langkah “mundur” tidak dapat dilakukan.
Pada saat yang sama, matriks pengurangan risiko pada awalnya dikaitkan dengan matriks "lama". Artinya, dalam gambar Anda dapat dan harus melayang "bolak-balik", tetapi dalam versi formal Anda tidak dapat berjalan "bolak-balik".
Masalah selanjutnya berkaitan dengan fakta bahwa risiko besar dengan probabilitas rendah dapat dibandingkan dengan risiko dari risiko kecil dalam jumlah sangat besar dengan probabilitas rendah.
Dalam contoh di atas, 7 peristiwa kecil tidak secara resmi menyebabkan kerusakan. Jelas bahwa ini bukan masalahnya. Tidak adanya risiko kecil hanya menekankan ketidaktepatan yang tidak memadai dari pembentukan Matriks Risiko.
Biarlah determinan Matriks Resiko tidak sama dengan nol dan ini merupakan konsekuensi dari kontinuitas pekerjaan untuk mengurangi resiko, dan bukan merupakan persyaratan artifisial dari metode matematika untuk bisnis.
Jadi, ada:
- Matriks risiko, yang sesuai dengan transformasi linier yang tidak diketahui dan dasar yang tidak diketahui;
- determinan Matriks, yang tidak sama dengan nol.
Apa yang bisa dilakukan? Membawa Matriks Risiko ke bentuk kanonik dengan dasar ortonormal yang dapat dimengerti.
Dalam karya Alexander Emelin, deskripsi alegoris berikut tentang keuntungan bentuk kanonik diberikan. “Misalkan ada selembar kertas dengan kata tertulis di atasnya. Tapi itu sangat rumit sehingga kata-katanya tidak bisa dilihat. Setelah transformasi kanonik, lembaran itu dibuka sedemikian rupa sehingga kata itu dapat dilihat. Jika dasar ortonormal digunakan, ukuran kertas akan tetap sama. "
Tidak ada operasi dan transformasi yang dijelaskan dalam karya ini yang mengubah esensi dari fenomena yang tercermin dan terkandung dalam Matriks Risiko.
4. Matriks risiko sebagai konstruksi aljabar.
Tugas utama kedua. Representasi kanonik.
Elemen ditambahkan ke matriks yang dipertimbangkan sehingga determinannya tidak sama dengan nol. Nilai dibulatkan untuk menghindari rumus yang terlalu besar.

Selanjutnya, menurut skema standar, matriks direduksi menjadi bentuk kanonik.
Nilai Eigen dari Risk Matrix.

Pekerjaan lebih lanjut dengan nilai-nilai simbolik akan sulit selama ortogonalisasi dan hasilnya tidak mungkin untuk divisualisasikan (matriks simbolik yang sangat rumit).
Misalkan (misalnya) d1 = 1, d2 = 2, d3 = 5, d4 = 8, d5 = 12.
Kemudian Risk Matrix M dalam representasi simetris mengambil bentuk.

Dicek bahwa determinan tidak sama dengan nol.
Nilai eigen dihitung.

Ditemukan matriks vektor eigen.

Itu ortogonal. Ini adalah matriks ORT dari vektor orthonormal.

Untuk memeriksa, vektor pertama (kolom) dikalikan berpasangan dengan yang lainnya. Nilainya bukan nol, tetapi mendekati 0.

Basis baru berisi representasi transformasi linier asli (mendefinisikan Matriks Risiko) dalam variabel z1, z2, z3, z4, z5.

Jika kita mengabaikan suku-suku yang sangat kecil, maka representasi kanonik dari transformasi linier diperoleh.

Selain itu, koefisien pada kuadrat sesuai dengan nilai eigen yang dihitung sebelumnya.
Tampilan baru Matriks Risiko dalam basis ortonormal.

Ternyata bentuk kuadrat bolak-balik.
5. Penggunaan praktis dari representasi kanonik.
Bagaimana dengan Risk Matrix yang asli?
Ini mewakili transformasi linier yang tidak diketahui.
Garisnya ditetapkan (dari atas ke bawah) sebagai x1, x2, x3, x4, x5. Baris Matriks Risiko mewakili dekomposisi dalam dasar yang tidak diketahui.
Jadi
x1 = 10 * d5 * b1 + 0 * b2 + 0 * b3 + 0 * b4 + 0 * b5,
x2 = 8 * d4 * b1 + 0 * b2 + 4 * d4 * b3 + 0 * b4 + 0 * b5 , dll.
Adanya basis ortonormal memberikan kebebasan bergerak antara variabel X dan Z.
Pada variabel Z, fungsi transformasi linier pada basis ortonormal terlihat jelas. Perilaku transformasi linier yang sama dalam Risk Matrix asli tidak jelas.
Manfaat yang jelas dari tampilan kanonik adalah kemampuan untuk menyesuaikan jenis ancaman. Jika awalnya klasifikasi berjalan dengan kelipatan 20%, sekarang dapat direvisi dengan menghitung ulang nilai akhir rentang dengan dasar baru. Juga akan ada 5 jenis acara, tetapi langkah-langkah di antaranya akan berbeda.
Manfaat yang jelas dari tampilan kanonik adalah kemampuan untuk menyesuaikan penskalaan untuk berbagai jenis peristiwa (insiden). Jika awalnya penskalaan peristiwa (sangat kuat, kritis, ...) mengikuti langkah 20%, sekarang dapat direvisi dengan menghitung ulang nilai akhir rentang dengan dasar baru. Juga akan ada 5 jenis peristiwa (insiden), tetapi langkah-langkah di antaranya akan berbeda.
6. Matriks Risiko: Bentuk kuadrat mendefinisikan konten.
Manfaat praktis yang dijelaskan mungkin tampak konyol dengan latar belakang manipulasi yang tidak cukup sederhana yang dilakukan sebelumnya: "permainan tidak sebanding dengan lilinnya."
Bentuk Matriks Risiko Google yang jelas, dapat dipahami, dan sederhana tidak sepenuhnya sesuai dengan konten manajemen risiko.
Apa risiko itu: Anda mengandalkan satu hal, tetapi kenyataannya Anda mendapatkan yang lain.
Matriks risiko Google dirancang sedemikian rupa sehingga perusahaan selalu mengetahui dengan jelas risikonya dan secara konsisten berupaya menguranginya. Selain itu, semua risiko tinggi dengan kerusakan besar secara bertahap dihilangkan. Pujian untuk manajer yang bijaksana.
Sebaliknya, Matriks Risiko yang diperoleh dengan basis ortonormal akan selalu menunjukkan adanya risiko tinggi yang tidak kosong.
Representasi kanonik yang dibentuk pada Bagian 4 dapat diartikan sebagai kerusakan yang terjadi ketika peristiwa yang diharapkan terjadi: variabel di dalam kotak.

Ada satu keadaan yang lebih penting. Kerusakan juga terjadi jika biaya dibuat untuk mencegah situasi yang tidak terjadi.
Desain baru berikutnya.

Nilai v [i, j] sesuai dengan kerusakan (manfaat), asalkan kita menghitung peristiwa f (j), tetapi peristiwa f (i) benar-benar terjadi. Nilai v [i, j] dapat berupa positif (merugikan) atau negatif (menguntungkan).
Nilai v [i, i] sesuai dengan situasi ketika acara yang kami persiapkan benar-benar terjadi: apa yang kami harapkan adalah apa yang kami dapatkan.
Dalam hal ini, Risk Matrix mengambil bentuknya.

Vektor kolom peristiwa memiliki bentuk.

Dalam hal ini, jumlah kerusakan digambarkan dengan bentuk kuadrat.

Konstruksi baru yang disajikan dari deskripsi risiko dapat dikaitkan dengan perhitungan berikut: penilaian kerusakan dalam kejadian aktual dari peristiwa f (i), sedangkan tindakan difokuskan pada peristiwa f (j).
Kemudian menjadi jelas apa “tindakan mitigasi risiko” yang diperlukan:
- untuk risiko yang tidak disiapkan, tetapi sering muncul;
- untuk risiko yang diidentifikasi sebagai dasar.
Selain itu, semua manipulasi aljabar yang dijelaskan di atas menjadi tidak hanya sesuai, tetapi juga wajib.
Masalah meminimalkan risiko dikurangi untuk meminimalkan nilai kerusakan yang diberikan oleh representasi kanonik dari bentuk kerusakan kuadrat.
7. Matriks risiko sebagai alat manajemen digital.
Dalam kasus umum, Anda dapat menggunakan berbagai metode penilaian dan manajemen risiko: pemodelan simulasi, sistem antrian, penilaian stabilitas skema struktural koneksi serial-paralel komponen, dan lain-lain.
Dalam hal ini, “genre” matriks risiko dan peluangnya untuk peningkatan bisnis dipertimbangkan.
Kenyataannya, bentuk baru ini memungkinkan Risk Matrix beralih dari peran "bogeyman" dan menjadi alat normal untuk manajemen bisnis digital. Salah satu dari sekian banyak untuk bisnis saat ini.
Untuk ini, perlu mengubah metodologi untuk menghitung kerusakan, dengan fokus pada nilai kuantitatif yang dapat diverifikasi versus berfokus pada penilaian ahli kualitatif.