Olimpiade Matematika. William Lowell Putnam Mathematical Competition adalah kompetisi matematika untuk mahasiswa sarjana yang belajar di universitas (kolese) di Amerika Serikat dan Kanada. Inspirasi untuk Olimpiade adalah William Lowell Putnam, seorang pengacara dan bankir Amerika. Diselenggarakan oleh Mathematical Association of America setiap tahun sejak 1938. Hadiah uang tunai diberikan kepada lima tim universitas teratas (hadiah juara pertama $ 25.000) dan dua puluh lima siswa teratas dalam kompetisi individu (hadiah juara pertama $ 1.000).
- Wikipedia
Olimpiade berlangsung dua kali selama 3 jam, total 12 soal, masing-masing 10 poin. Nilai rata-rata yang diperoleh siswa adalah 1 atau 2. Mari kita pertimbangkan salah satu masalah tersulit dari Olimpiade ini.
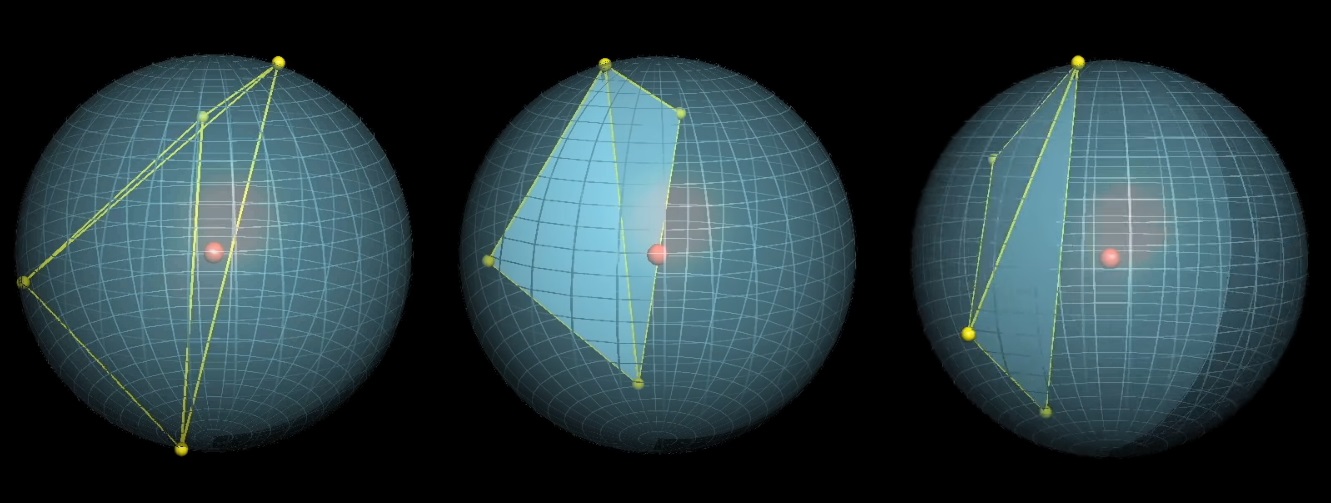
Pilih 4 titik acak di bola. Berapakah probabilitas bahwa pusat bola akan berada di dalam tetrahedron yang dibentuk oleh titik-titik ini?
Mari kita pertimbangkan versi dua dimensi dari masalah ini.
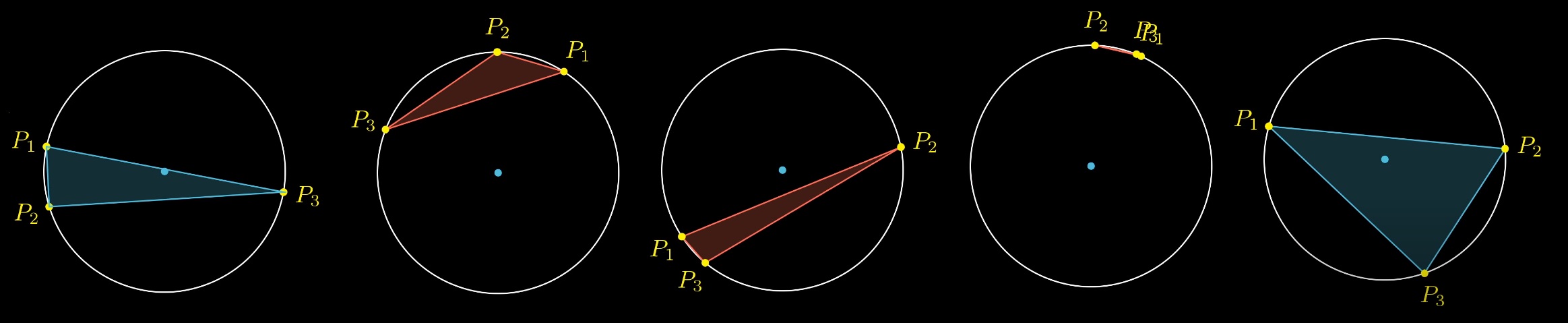
Pertimbangkan 3 titik acak pada sebuah lingkaran. Berapa probabilitas bahwa pusat lingkaran akan berada di dalam segitiga?

Anda dapat menyematkan dua poin dan bermain dengan poin ketiga. Sangat mudah untuk melihat bahwa ada zona tertentu, proyeksi titik berlabuh relatif terhadap pusat, di dalamnya titik ketiga harus jatuh agar kondisi tersebut terpenuhi. Lingkaran tersebut kemudian dibagi menjadi 4 bagian. Probabilitas mengenai titik ketiga dalam busur sama dengan rasio panjang busur dengan keliling. Berapa panjang busurnya?
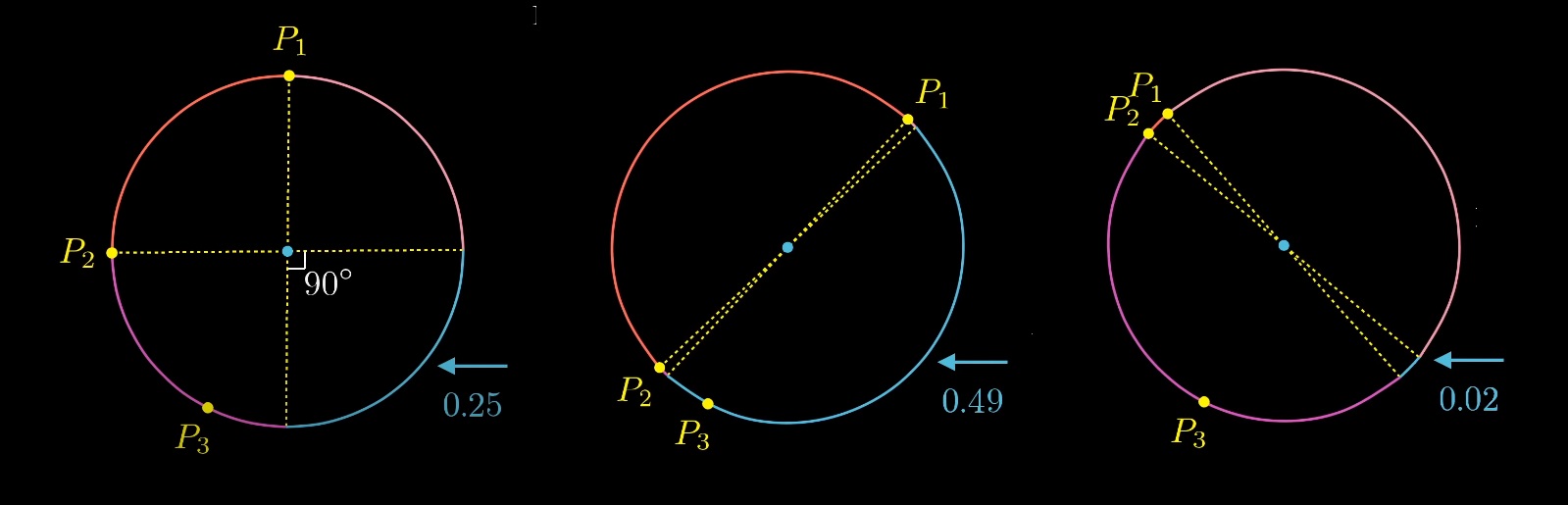
Probabilitasnya berkisar dari 0 hingga 0,5 tergantung pada lokasi dua poin pertama.
Berapa probabilitas rata-ratanya?

Mari kita perbaiki poin pertama dan mainkan dengan poin kedua. Probabilitas akan bervariasi dari 0 hingga 0,5, yaitu probabilitas rata-rata akan menjadi 0,25.
Memecahkan masalah untuk lingkaran dan tiga poin - 25%.
Apakah mungkin untuk mentransfer pendekatan ini ke bola dan 4 poin?
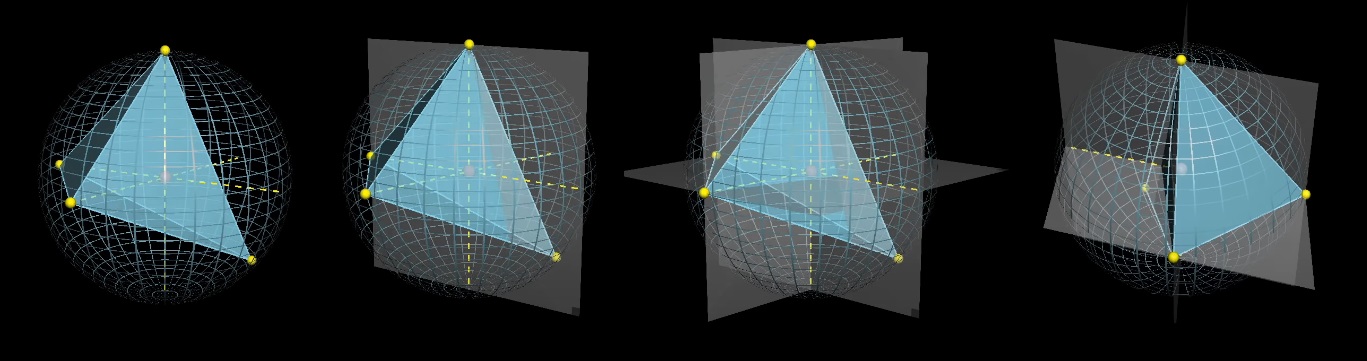
Kami memperbaiki tiga poin dan bermain dengan yang keempat. Mari menggambar proyeksi titik tetap relatif terhadap pusat dan membagi bola menjadi 8 bagian dengan bidang.
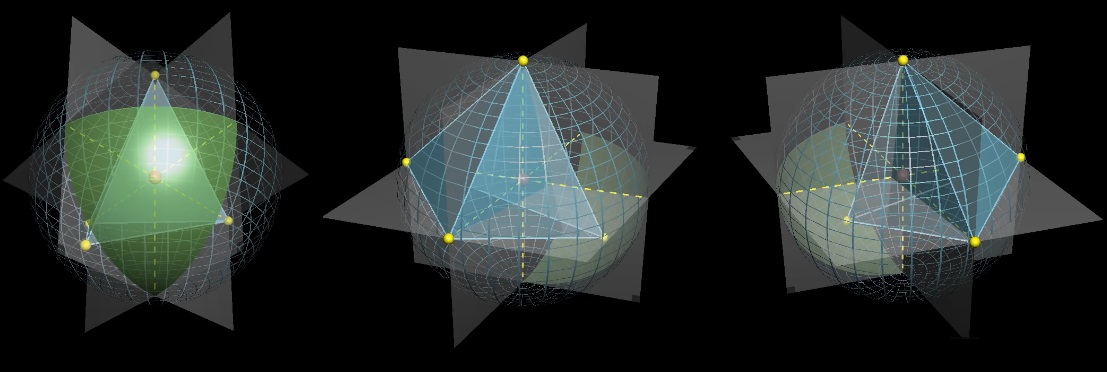
Pusat bola akan berada di dalam tetrahedron jika titik keempat jatuh pada segitiga bola hijau, yang "berlawanan" dengan titik tetap yang relatif terhadap pusat. Berapa ukuran rata-rata bagian hijau?
// Jangan memikirkan lebih jauh, berimprovisasi.
Anda dapat kembali ke kasus dua dimensi dan memikirkan tentang dari mana 1/4 berasal. Dari mana 4 berasal?
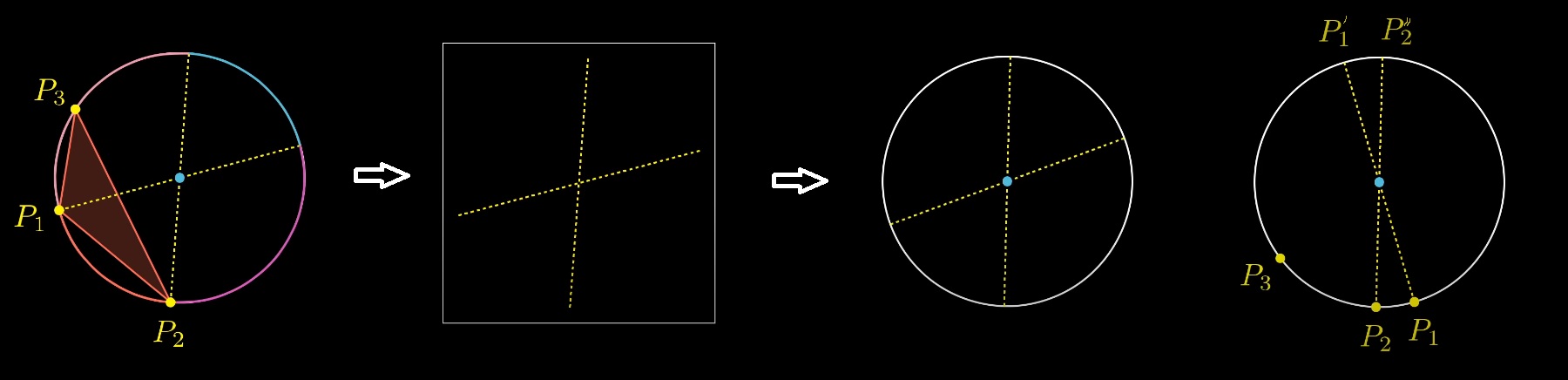
Anda dapat beralih dari 3 titik acak pada lingkaran ke soal lain. Mari pilih dua diameter acak. Kemudian untuk setiap diameter kita melempar koin, dengan demikian memilih di mana titik Pi akan berada, dari ujung diameter mana. Kemudian kami secara acak memilih titik ketiga pada lingkaran.
Dan kemudian gerakan licik lainnya.
Mari pertama-tama pilih titik ketiga secara acak dan kemudian pilih dua diameter secara acak. Kami akan memiliki 4 opsi untuk menempatkan poin P2 P1:
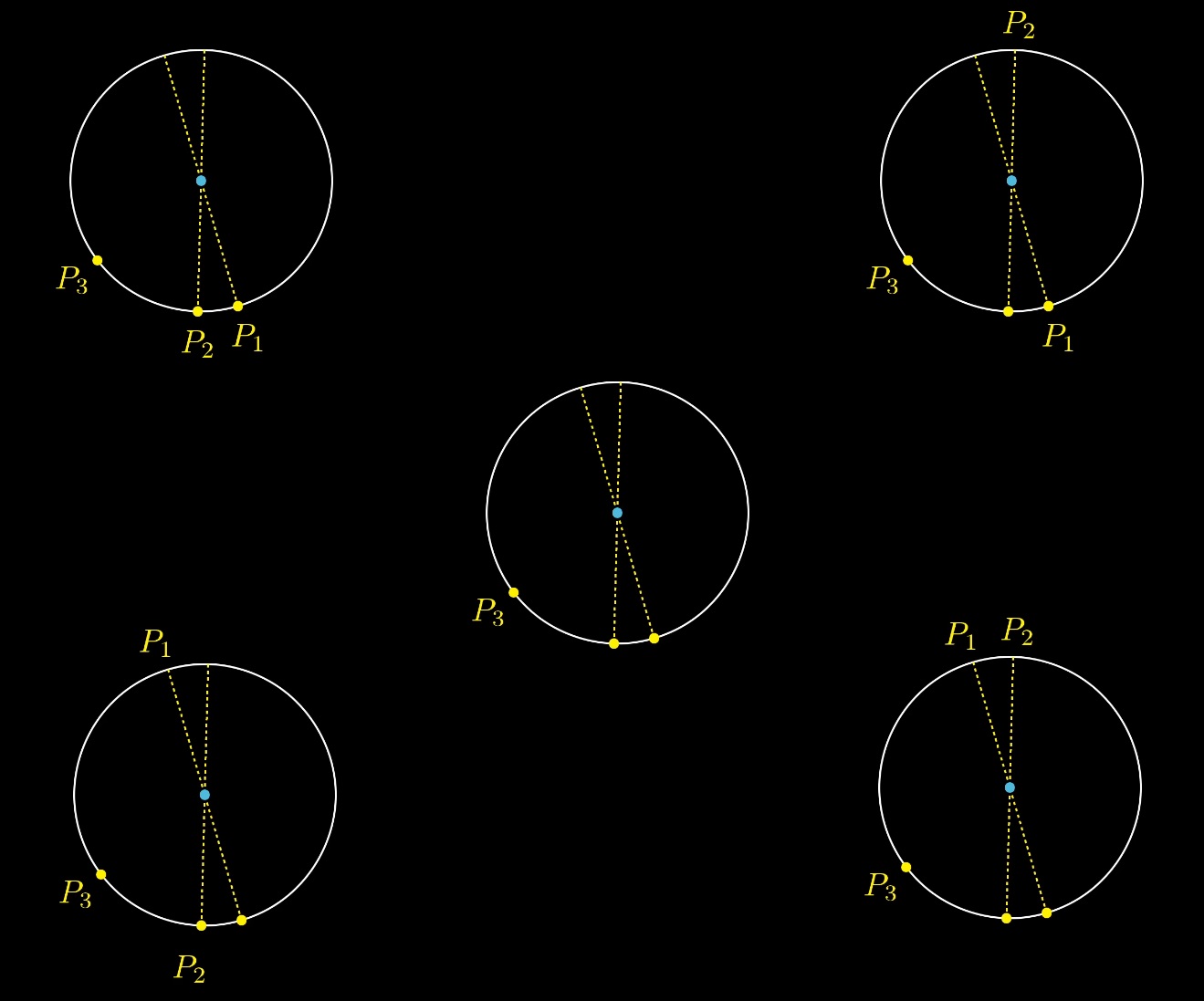
Tetapi hanya satu dari 4 opsi ini yang berisi solusi ketika pusat lingkaran berada di dalam segitiga:
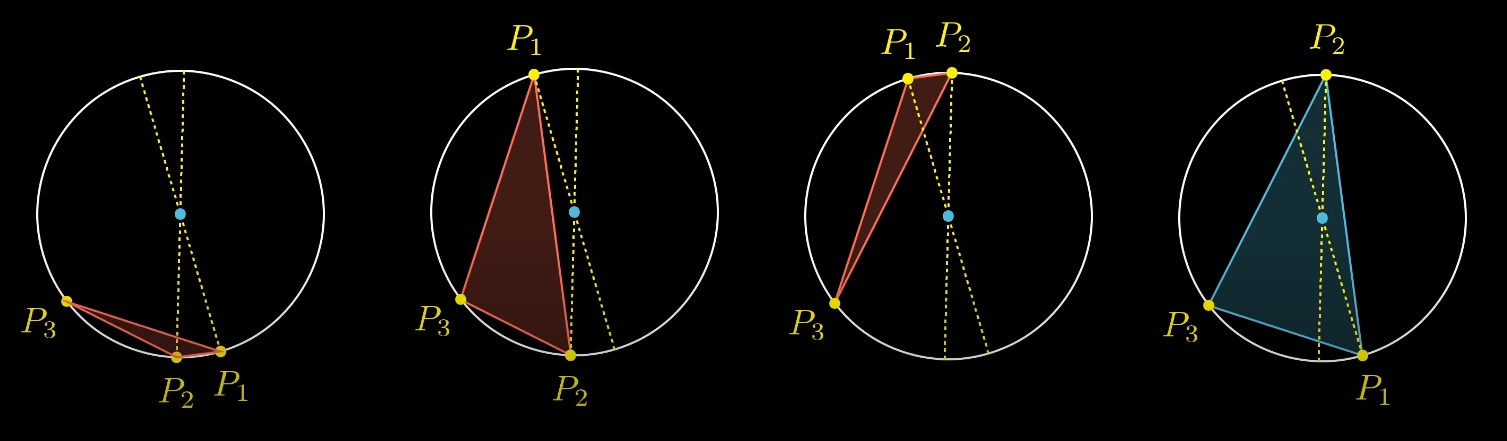
Apapun yang kami pilih posisi awal acak dari titik ketiga dan dua diameter, hanya satu opsi yang berisi pusat lingkaran di dalam segitiga:

Begitulah cara kami merumuskan kembali masalah:

Dengan bola, kami mendapatkan 8 opsi untuk memilih titik, setelah titik pertama ditetapkan dan tiga diameter dipilih:
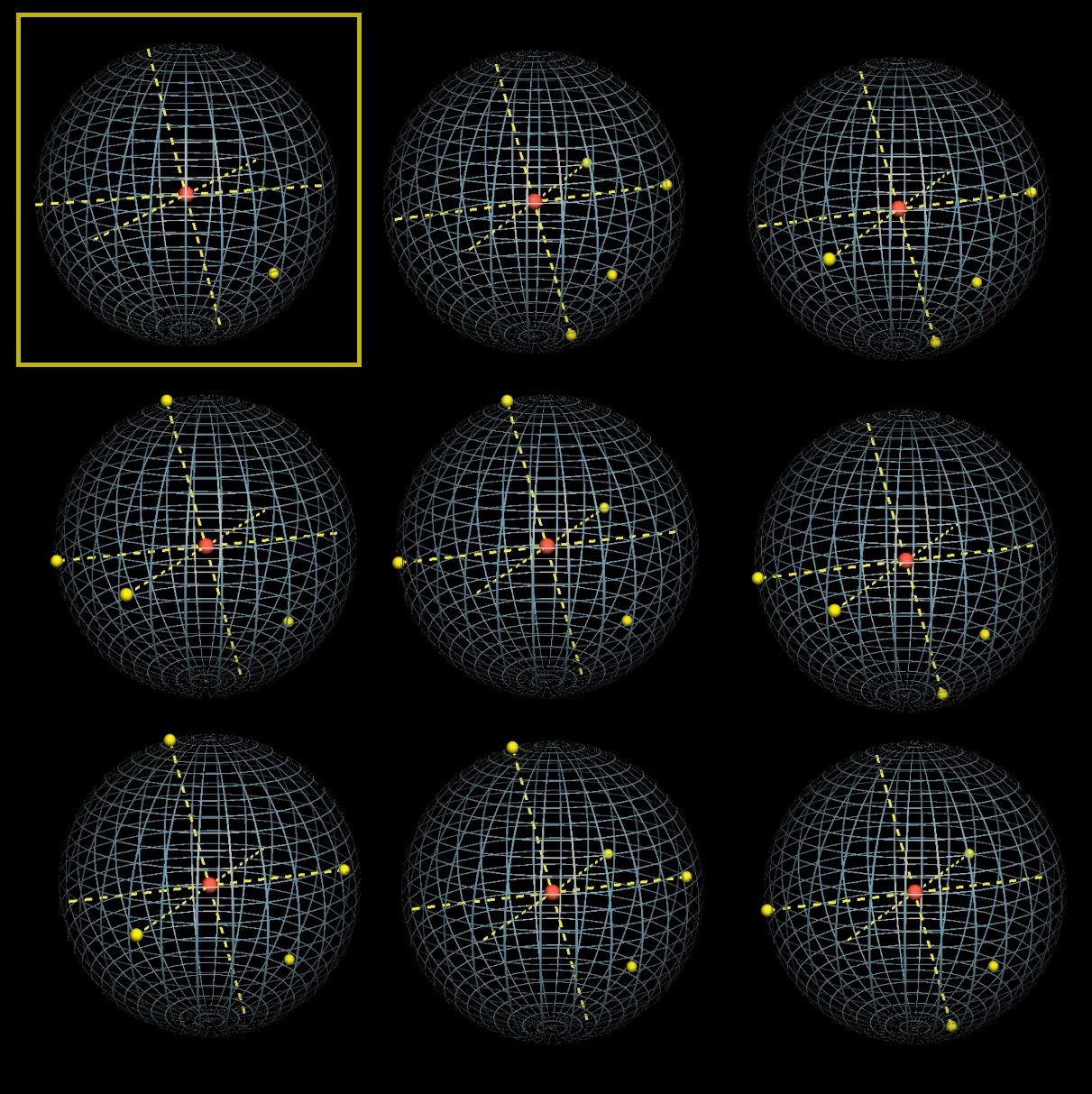
Hanya 1 dari 8 yang memenuhi syarat bahwa pusat bola berada di dalam tetrahedron:
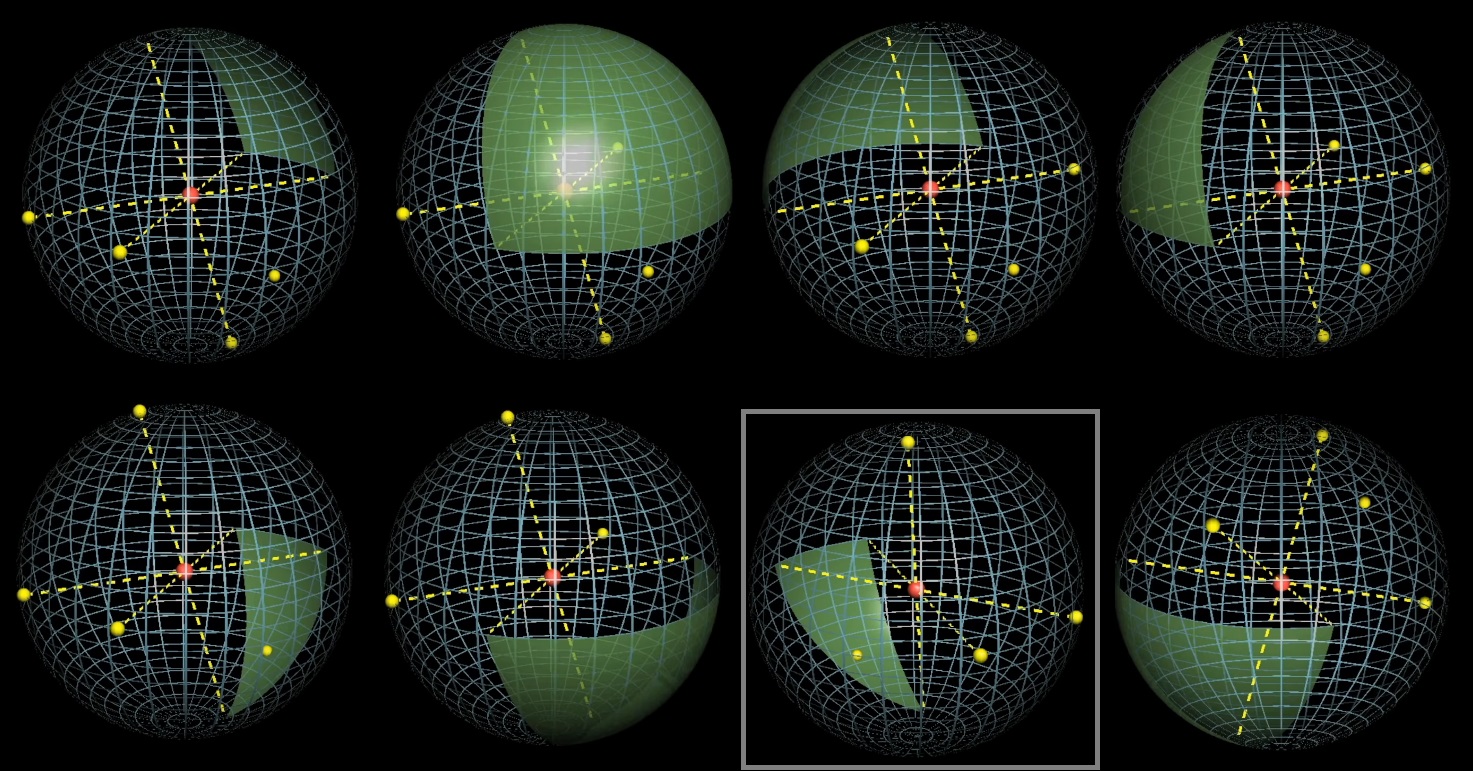
Jawaban: 1/8
- Aljabar linier hardcore ada di sini: Menangkap Asal dengan Titik Acak: Generalisasi Masalah Putnam
- Semua soal Olimpiade 1992: Kompetisi Matematika William Lowell Putnam ke-53
Sabtu, 5 Desember 1992