
Jadi, pertimbangkan grafik berbobot terarah. Biarkan grafik memiliki n simpul. Setiap pasangan simpul berhubungan dengan beberapa bobot (probabilitas transisi).

Perlu dicatat bahwa grafik web tipikal adalah rantai Markov diskrit homogen yang kondisi indekomposabilitas dan kondisi aperiodisitasnya terpenuhi.
Mari kita tulis persamaan Kolmogorov-Chapman: dengan
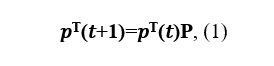
P adalah matriks transisi.
Misalkan ada batasan
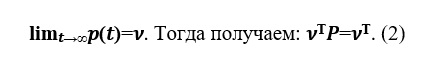
Vektor v disebut distribusi probabilitas stasioner.
Dari relasi (2) diusulkan untuk mencari vektor rangking halaman web dalam model Brin-Page.
Karena v adalah batasnya,

distribusi stasioner dapat dihitung dengan metode iterasi sederhana (MPI).
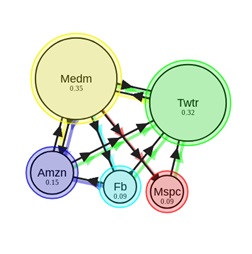
Untuk berpindah dari satu halaman web ke halaman web lainnya, pengguna harus, dengan kemungkinan tertentu, memilih tautan mana yang akan dituju. Jika dokumen memiliki beberapa tautan keluar, maka kami akan mengasumsikan bahwa pengguna mengklik masing-masing tautan dengan probabilitas yang sama. Dan terakhir, ada juga koefisien teleportasi, yang menunjukkan kepada kita bahwa dengan kemungkinan tertentu pengguna dapat berpindah dari dokumen saat ini ke halaman lain, tidak harus terkait langsung dengan halaman tempat kita berada saat ini. Biarkan pengguna melakukan teleportasi dengan probabilitas δ, maka persamaan (1) akan berbentuk.

Untuk 0 <δ <1, persamaan tersebut dijamin memiliki solusi yang unik. Dalam praktiknya, persamaan dengan δ = 0,15 biasanya digunakan untuk menghitung PageRank.
Pertimbangkan grafik web Google dari situs - tautan. Grafik web ini berisi 875713 simpul, yang berarti untuk matriks dua dimensi P, Anda perlu mengalokasikan memori 714 Gb. RAM komputer modern adalah urutan besarnya lebih kecil, sehingga komputer mulai menggunakan memori hard disk, akses yang sangat memperlambat kerja program kalkulasi PageRank. Tetapi matriks P adalah matriks renggang - matriks dengan sebagian besar elemen nol. Untuk bekerja dengan matriks renggang dengan Python, modul renggang dari pustaka scipy digunakan, yang membantu matriks P menggunakan lebih sedikit memori.
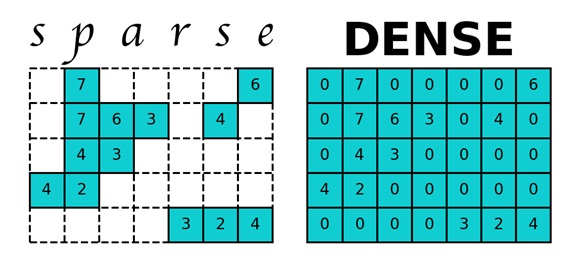
Mari terapkan algoritma ini pada data ini. Node mewakili halaman web, dan tepi terarah adalah hyperlink di antara mereka.
Pertama, mari impor pustaka yang kita butuhkan:
import cvxpy as cp
import numpy as np
import pandas as pd
import time
import numpy.linalg as ln
from scipy.sparse import csr_matrix
Sekarang mari beralih ke implementasinya sendiri:
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
#
p0 = np.ones((NODES,1))/NODES
eps = 10**-5
delta = 0.15
ERROR = True
k = 0
#
while (ERROR == True):
with np.errstate(divide='ignore'):
z = p0 / b
p1 = (1-delta) * NEW.dot(csr_matrix(z)) + delta * np.ones((NODES,1))/NODES
if (ln.norm(p1-p0) < eps):
ERROR = False
k = k + 1
# PageRank
p0 = p1
Pada grafik kita dapat melihat bagaimana vektor p menjadi stasioner v :

Menggunakan vektor PageRank, kita juga dapat menentukan pemenang dalam pemilihan. Sebagian kecil kontributor Wikipedia adalah administrator, yang merupakan pengguna dengan akses ke fitur teknis tambahan untuk membantu pemeliharaan. Agar pengguna menjadi administrator, permintaan administrator dikeluarkan, dan komunitas Wikipedia, melalui komentar publik atau pemungutan suara, memutuskan siapa yang akan dipromosikan ke posisi administrator.
Masalah PageRank juga dapat direduksi menjadi masalah minimisasi dan diselesaikan dengan menggunakan metode gradien bersyarat Frank - Wolfe, yaitu sebagai berikut: pilih salah satu simpul simplex dan buat titik awal pada simpul ini. Implementasi metode ini pada data - tautannya disajikan di bawah ini:
#
data = pd.read_csv("grad.txt", names = ['i','j'], sep="\t", header=None)
NODES = 6301
EDGES = 20777
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
e = np.ones(NODES)
with np.errstate(divide='ignore'):
z = e / b
NEW = NEW.dot(csr_matrix(z))
#
eps = 0.05
k=0
a_0 = 1
y = np.zeros((NODES,1))
p0 = np.ones((NODES,1))/NODES
#
p0[0] = 0.1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y
#
while ((ln.norm(p1-p0) > eps)):
y = np.zeros((NODES,1))
k = k + 1
p0 = p1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y

Untuk pengoperasian mesin telusur yang efektif secara efektif, kecepatan penghitungan vektor PageRank lebih penting daripada keakuratan penghitungannya. MPI tidak mengizinkan Anda mengorbankan akurasi demi kecepatan komputasi. Algoritma Monte Carlo membantu mengatasi masalah ini sampai batas tertentu. Kami meluncurkan pengguna virtual yang menjelajahi halaman situs. Dengan mengumpulkan statistik kunjungan mereka ke halaman situs, setelah jangka waktu yang cukup lama kami mendapatkan berapa kali pengguna telah mengunjunginya untuk setiap halaman. Dengan menormalkan vektor ini, kita mendapatkan vektor PageRank yang diinginkan. Mari kita tunjukkan bagaimana algoritma ini bekerja pada data yang sudah digunakan .
#
def get_edges(m, i):
if (i == NODES):
return random.randint(0, NODES)
else:
if (len(m.indices[m.indptr[i] : m.indptr[i+1]]) != 0):
return np.random.choice(m.indices[m.indptr[i] : m.indptr[i+1]])
else:
return NODES
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
#c , total –
for total in range(1000000,2000000,100000):
#
k = random.randint(0, NODES)
# PageRank
ans = np.zeros(NODES+1)
margin2 = np.zeros(NODES)
ans_prev = np.zeros(NODES)
for t in range(total):
j = get_edges(NEW, k)
ans[j] = ans[j]+1
k = j
#
ans = np.delete(ans, len(ans)-1)
ans = ans/sum(ans)
for number in range(len(ans)):
margin2[number] = ans[number] - ans_prev[number]
ans_prev = ans
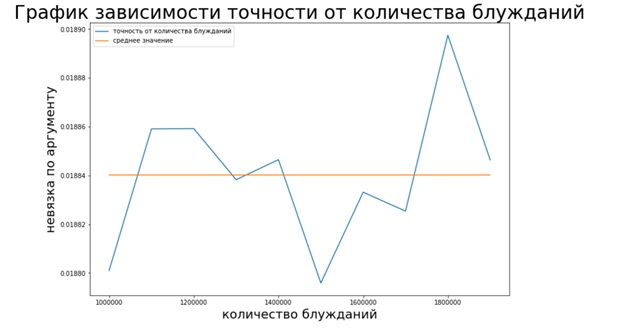
Seperti yang dapat dilihat dari grafik, metode Monte Carlo, tidak seperti dua metode sebelumnya, tidak stabil (tidak ada konvergensi), namun, metode ini membantu untuk memperkirakan vektor Page Rank tanpa memerlukan banyak waktu.
Kesimpulan: Dengan demikian, kami telah mempertimbangkan algoritma utama untuk menentukan PageRank dari grafik web. Sebelum Anda mulai mendesain situs web, Anda harus memastikan bahwa PageRank tidak sia-sia dengan memperhatikan hal-hal berikut:
- Tautan internal menunjukkan bagaimana "kekuatan tautan" terakumulasi di situs Anda, jadi fokuslah pada informasi penting di beranda situs, karena laman "beranda" situs memiliki PageRank terkuat.
- Halaman yatim piatu yang tidak ditautkan dari halaman lain di situs Anda. Cobalah untuk menghindari halaman seperti itu.
- Perlu disebutkan tautan eksternal jika bermanfaat bagi pengunjung situs Anda.
- Tautan masuk yang rusak mengurangi berat keseluruhan laman, jadi Anda perlu memantaunya secara berkala dan "memperbaikinya" jika perlu.
Namun, ini tidak berarti Anda harus terobsesi dengan PageRank. Tetapi perlu diingat bahwa dengan memperhatikan struktur situs saat membangunnya, fitur tautan internal dan eksternal, Anda mengoptimalkan situs untuk PageRank.