“Saya baru-baru ini mulai bereksperimen dengan gnuplot dan dengan cepat membuat penemuan yang menarik. Saya memplot semua bilangan prima di bawah 1 juta dalam koordinat kutub, jadi untuk setiap bilangan prima p (r, θ) = (p, p). Saya tidak mengharapkan sesuatu yang istimewa, saya hanya mencobanya. Hasilnya mengesankan. "
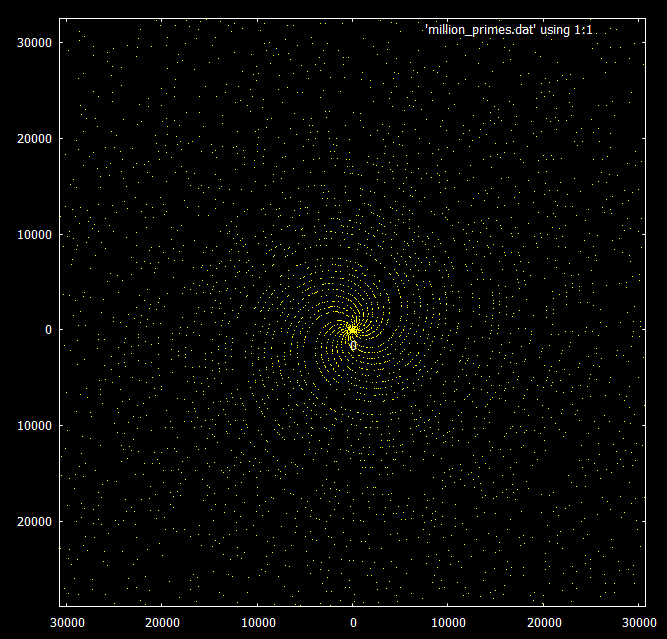
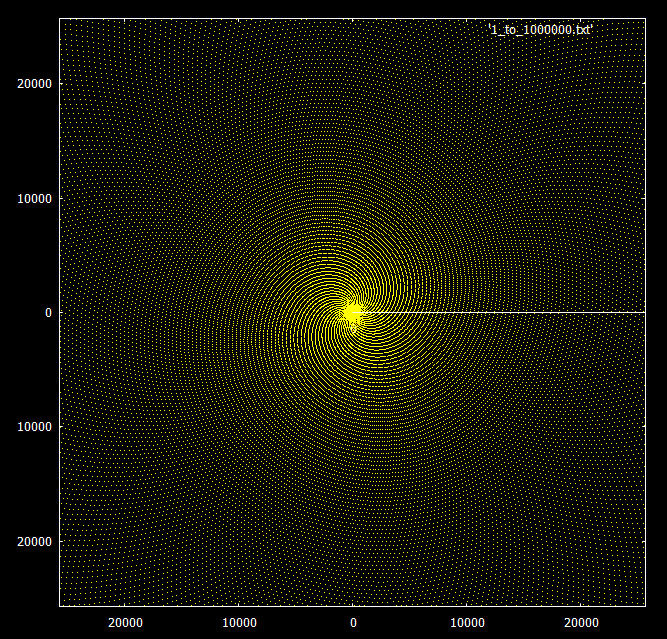
Jika Anda melihat bilangan prima di bawah 30.000, Anda dapat melihat pola spiral.
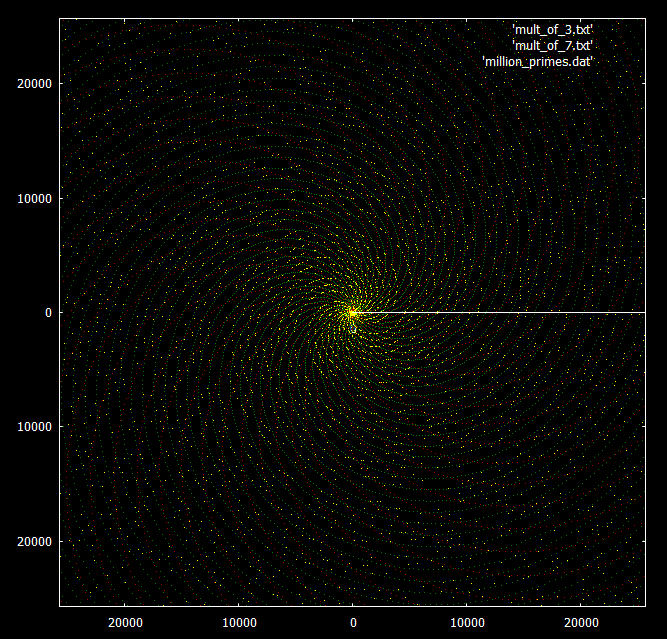
Sebagai perbandingan - grafik yang sama dengan bilangan yang ditumpangkan, kelipatan 3 dan 7. Bilangan prima disorot dengan warna kuning, kelipatan 3 dan 7 - masing-masing berwarna hijau dan merah.

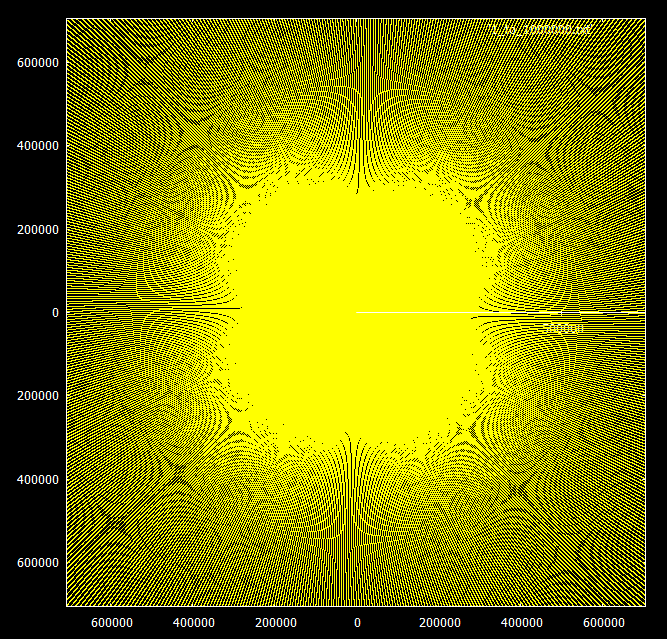
Yang sangat menarik adalah perilaku saat meningkatkan jangkauan. Kelipatan bilangan ini tampak seperti spiral dalam pola yang sama hingga tak terhingga, tetapi bilangan prima mulai membentuk sinar dalam kelompok 3 atau 4.
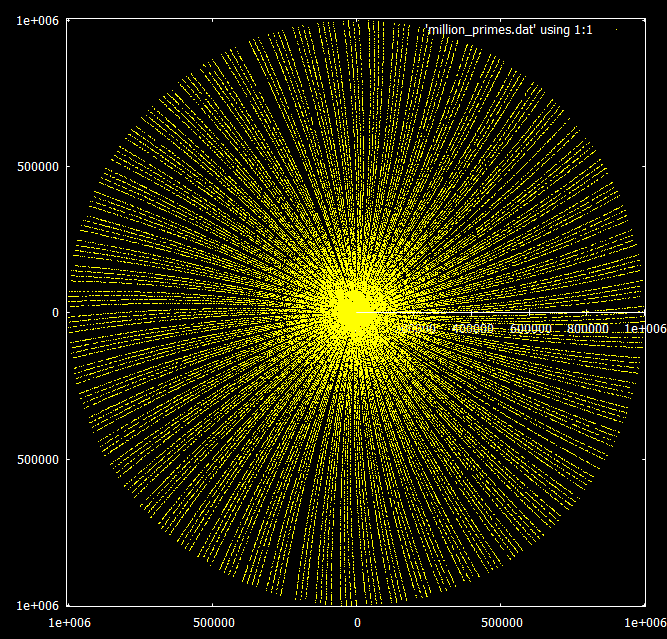
Dibandingkan dengan kelipatan 3 dan 7:
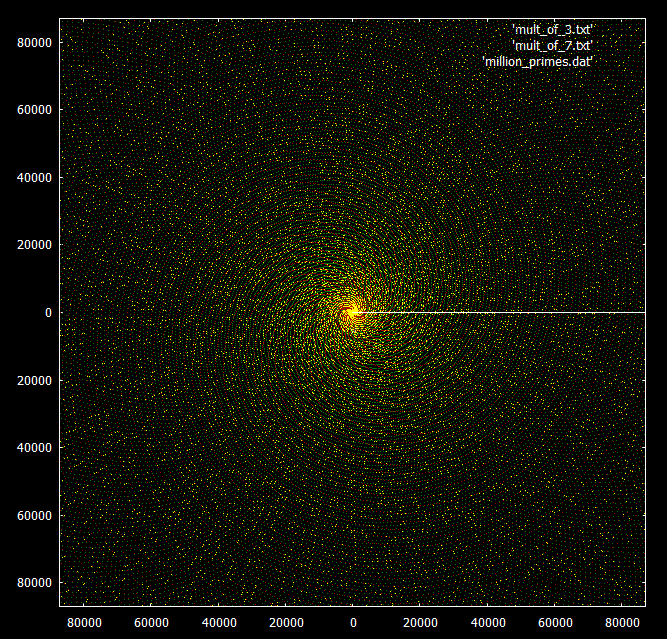
? , ?
. , , .
(, θ) = (n, n), n∈N
Untuk memulainya, Anda bisa bermain dengan koordinat kutub dan mempertimbangkan semua titik dengan koordinat integer: (1,1) (2,2) ...
Kita
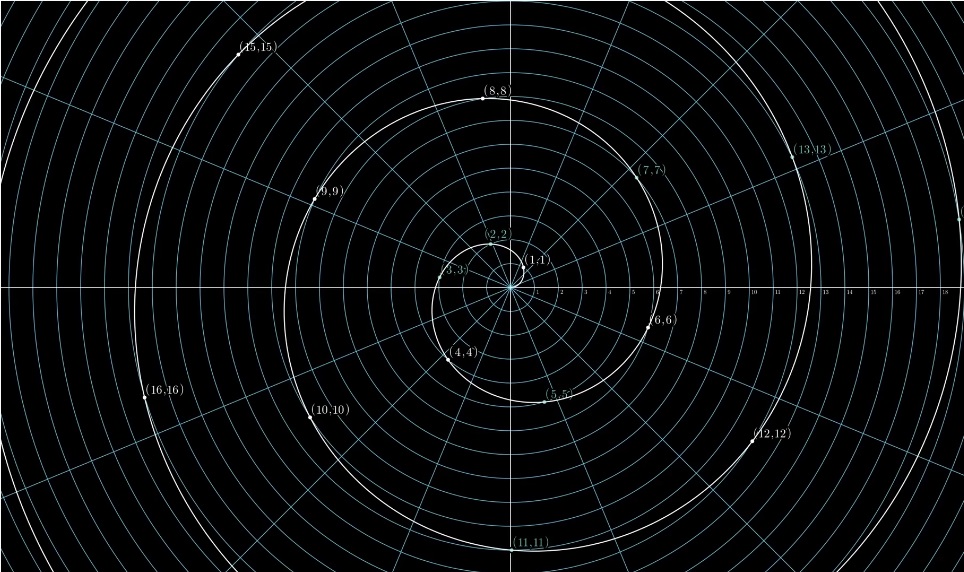
mendapatkan Spiral Archimedean: Jika kita mengecualikan semua bilangan kecuali bilangan prima, kita mendapatkan galaksi spiral dengan spasi:
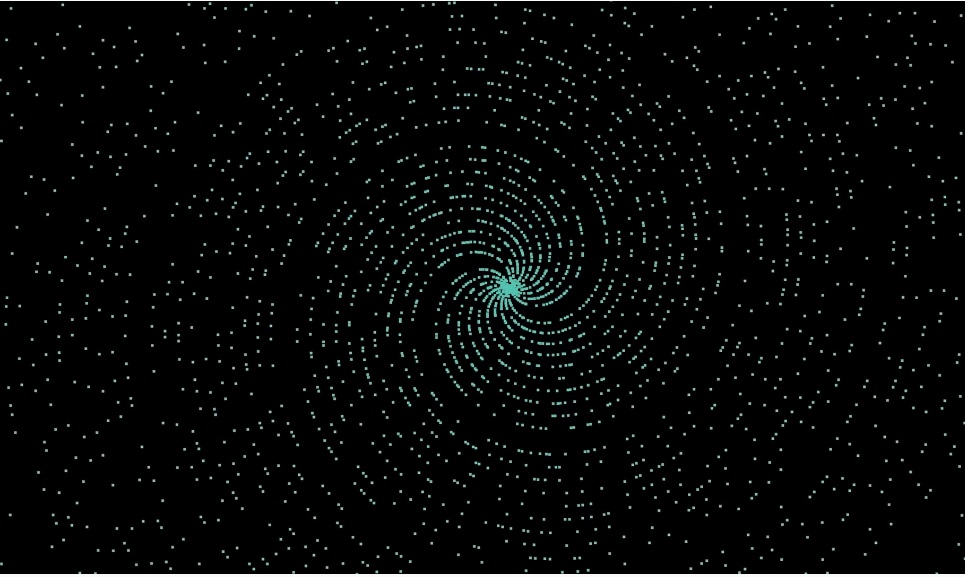
"Menjauh" kita bisa untuk melihat sinar yang diarahkan ke segala arah, kebanyakan dalam kelompok 4:

Spiral dapat dihitung ada 20 diantaranya:

Dan sinar 280:

Jika kita ambil semua bilangan, tidak hanya yang sederhana, maka spiral itu bahkan lebih genap dan ada 44: Jika

diamati lebih dekat, kita memiliki 6 spiral:

Semua bilangan yang merupakan kelipatan 6 membentuk satu cabang:
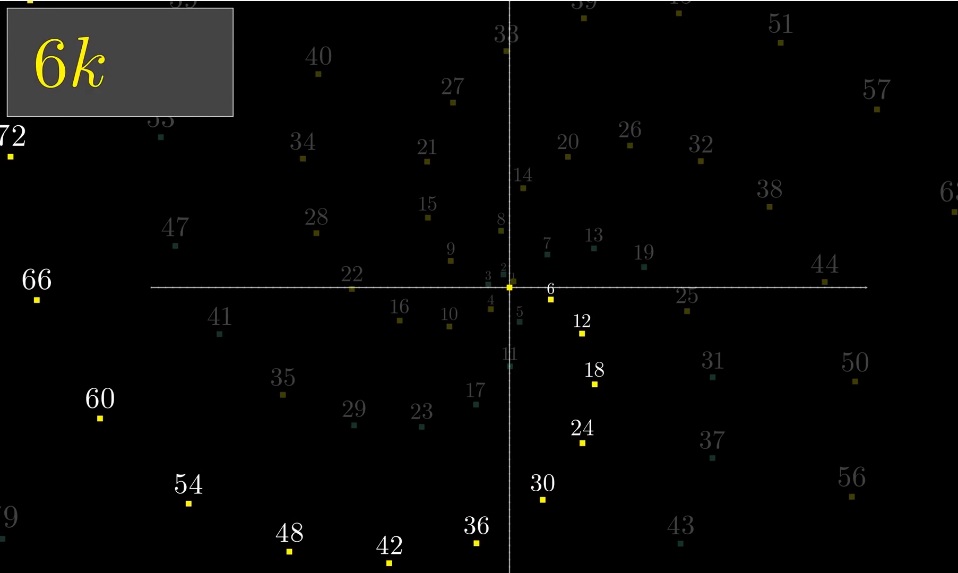
Sisa lengan spiral adalah 6k + 1, 6k + 2, dll. Mengapa demikian? Karena 6 kira-kira sama dengan (revolusi penuh) 2ℼ (6.28318530718). Perbedaan kecil ini menciptakan ilusi kurva tunggal.
Jika Anda meninggalkan hanya bilangan prima, hanya akan ada dua spiral (6k + 1 dan 6k + 5):
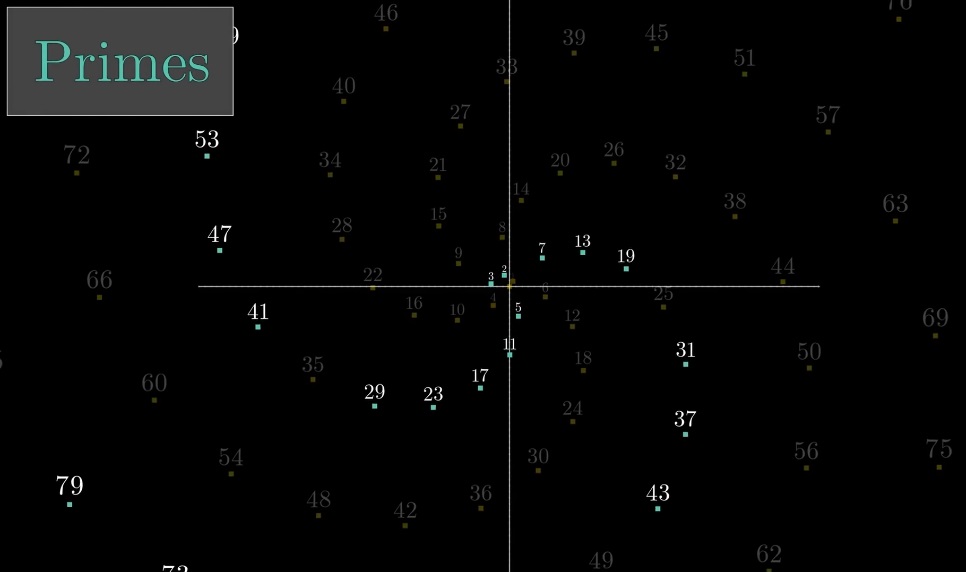
6 - hampir lingkaran penuh, 44 - perkiraan yang lebih akurat (44 / 2ℼ ≈ 7 lingkaran penuh)
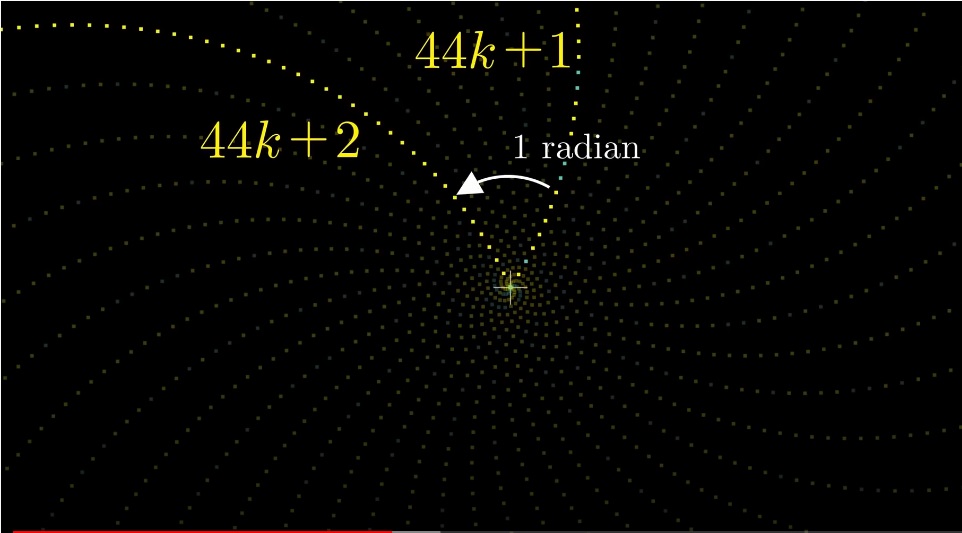
Hanya untuk bilangan prima ada 20 lengan (44k +1, 44k + 3, 44k + 5 ...). Fungsi Euler φ (44) = 20.

710 / 2ℼ ≈ 113. (113.00000959)

Untuk bilangan prima akan ada celah:

Semakin jauh kita menjauh, semakin jelas kelengkungan seluruh struktur menjadi jelas.
710 = 71 * 5 * 2. Hal ini menjelaskan pengelompokan 4 balok (5) dan "gigi sisir yang patah" (71):

Fungsi Euler φ (710) = 280.
Menurut teorema Dirichlet, bilangan prima didistribusikan secara merata di atas lengan baju.
Kesimpulan
Bermain dengan visualisasi, Anda dapat menemukan a) Prinsip Dirichlet b) mendekati bilangan ℼ (dan pecahan lanjutan) c) mencapai fungsi Euler.
Bentuk spiral adalah artefak yang terkait dengan jumlah genap radian yang cocok.
Film dengan akting suara Rusia:
PS
Lebih banyak pekerjaan tentang bilangan prima:
- Celah yang dibatasi antara bilangan prima . (Oleh Yitang Zhang, 2014)
- Primes dalam tuple I (Oleh DANIEL A.GOLDSTON, JÁNOS PINTZ, dan CEM Y. YILDIRIM, 2009)
Pecahan lanjutan dari Savvateev:
Alexey Savvateev "Semua tentang menulis angka":