
Selamat siang!
Di dunia modern, semakin banyak pernyataan tentang potensi ancaman dari komputer kuantum dalam kaitannya dengan protokol kriptografi yang digunakan. Komputer kuantum sudah mampu memecahkan masalah logaritma diskrit dan faktorisasi angka, yang mengancam semua protokol yang berbasis padanya.
Hari ini kita akan mempertimbangkan protokol NewHope, yang didasarkan pada tugas sulit lainnya - masalah pembelajaran dengan kesalahan dalam sebuah ring (Ring-LWE).
NewHope – , , . , SIS, LWE Ring-LWE:
1. SIS
SIS (Short integer solution problem) – .
, n q ( ):
A:

( ) , .
, ,
. , , .
, z,
. z ( q). , , . , .
? , ( ).
- . z.
, z A .
, , n - .
2. LWE ( Learning with errors)
:
:
n – ;
q – , . n, ;
, );
;
k, .
, , s
. ( q):
.
, (LWE on lattices).
:

– .
, q. .
, , :
:
.
3.
LWE, - SIS:
Public key encryption (LWE):
, . – .

,
0, 0, 1.
?
.
, , 4 , .
One-way function (SIS):
- -:

, . . (IV).
, ,
.
- (One-way function):
, :
.
-
:
SIS.
? , SIS .
4.
:
.
15 :

2) / , .
?
5. Ring-LWE
.
? , LWE . , n ?
?
– ,
, n – .
c q.
? . , , : . .
/? , 2 ,
LWE , , .
6. NewHope
, NewHope , Bos, Castello, Naehrig Stebila. TLS Ring-LWE.
, NewHope.
, .

:
, .
n = 1024, q = 12289 ( ,
). NTT ( ), n – , q – , .
a. : seed – 256 , SHAKE-128 ( SHA3). , 1024 a. : , TLS ( 2 ), NewHope , a. , backdoor , “” .
– , . - , ( ). seed /dev/urandom 16- . s e.
( b, seed).
a, s’, e’, e”, u.
v, , . .
,
, , . , – , 0
. , .
. : . q ,
.
( ).
. .
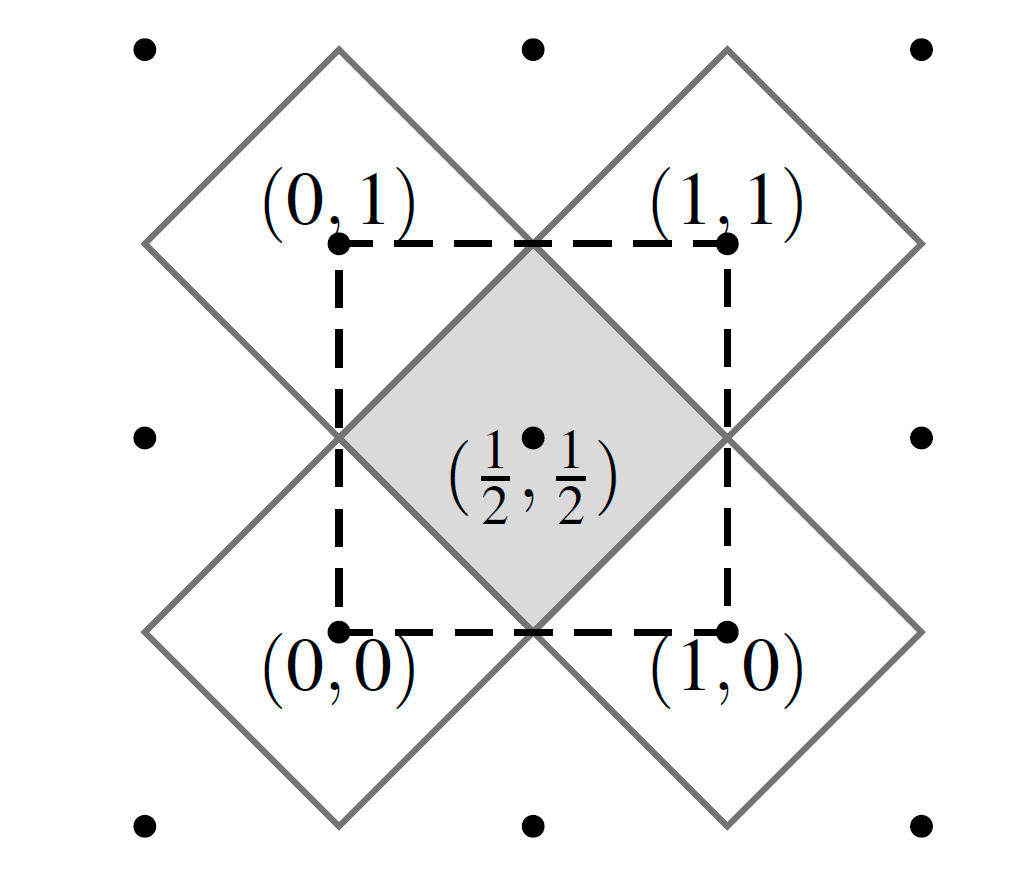
. , , : , 1, , 0. , , . HelpRec, . . , , .
8. Rec 1 4 ( ).
9. 256 , , .
7.
2019 NIST post-quantum crypto project, , . NIST , , KYBER ( Module-LWE) , . 3 KYBER.
, Google Canary CECPQ1 CECPQ2.
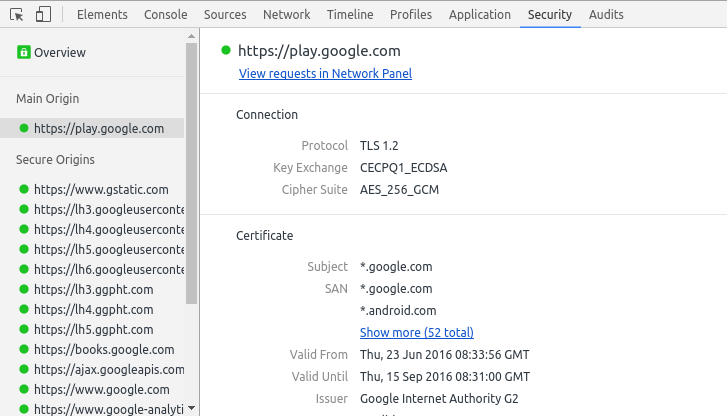
:
:
-
https://eprint.iacr.org/2015/1092.pdf
https://eprint.iacr.org/2014/599.pdf
https://www.di.ens.fr/chloe.hebant/presentation/SISproblem.pdf
http://www.ee.cityu.edu.hk/~twhk05/achieve/Wai%20Ho%20Mow.pdf
https://simons.berkeley.edu/talks/lwe-worst-case-average-case-reductions-and-cryptomania
https://simons.berkeley.edu/talks/algebraic-lattices-and-ring-lwe
https://www.ei.ruhr-uni-bochum.de/media/sh/veroeffentlichungen/2013/08/14/lwe_encrypt.pdf
-
https://people.csail.mit.edu/vinodv/6876-Fall2015/L12.pdf
https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html