Roger Penrose adalah penerima Hadiah Nobel Fisika 2020 "atas penemuannya bahwa pembentukan lubang hitam adalah prediksi relativitas umum yang andal."
Juga, Hadiah Nobel Fisika dianugerahkan kepada Reinhard Henzel dan Andrea Gez "atas penemuan benda kompak supermasif di pusat galaksi kita".
Roger Penrose adalah anggota Royal Society of London. Dia bekerja di berbagai bidang matematika, relativitas umum, dan teori kuantum. Penrose adalah penulis teori yang berkaitan dengan kesadaran kuantum, lompatan kuantum, biologi kuantum, dan penulis buku Fashion, Faith, Fantasy and the New Physics of the Universe, yang diterbitkan oleh Peter Publishing House.
Fashion, Faith, Fantasy dan New Physics of the Universe didasarkan pada tiga ceramah yang diberikan oleh Penrose di Universitas Princeton. Penulis sendiri mengakui bahwa biasanya fashion, fantasi dan keyakinan sama sekali tidak mengganggu orang yang serius mempelajari prinsip-prinsip dasar alam semesta. Kami akan menyerahkan iman kepada gereja, fashion ke fashion show, fantasi untuk penulis. Roger Penrose membuktikan di 500 halaman bahwa kata-kata romantis ini bisa menjadi penting dalam pencarian fondasi alam semesta.
Fantasi
3.1. Big Bang dan Friedman Universe
Bisakah fantasi memainkan peran non-ilusi dalam upaya kita untuk memahami realitas fisik? Tentu saja fantasi adalah kebalikan dari sains, dan tidak memiliki tempat dalam wacana ilmiah yang serius. Namun, tetap ada perasaan bahwa masalah ini tidak semudah yang terlihat - banyak proses alami akan tampak fantastis jika kita melanjutkan dari kesimpulan bahwa pengalaman ilmiah rasional berdasarkan penelitian eksperimental yang dapat diandalkan dapat mengarahkan kita. Seperti yang kita lihat, terutama di bab sebelumnya, dunia benar-benar diatur dengan cara yang paling fantastis jika kita mempelajarinya di tingkat mikro, di mana fenomena kuantum berkuasa. Objek material tertentu dapat berada di beberapa tempat dan, seperti vampir yang luar biasa (mampu berubah dari kelelawar menjadi manusia dan kembali lagi kapan pun dia mau),itu dapat menunjukkan baik sifat korpuskuler atau gelombang seolah-olah dengan pilihannya sendiri. Selain itu, "perilakunya" mengikuti bilangan misterius, yang mengandung akar kuadrat imajiner -1.
Selain itu, dalam skala yang sangat besar, fenomena ditemukan lagi, banyak di antaranya mungkin tampak fantastis - bahkan mungkin lebih mencolok daripada semua penemuan fiksi sastra. Misalnya, kadang-kadang tabrakan diamati antara seluruh galaksi, dan kita harus berasumsi bahwa mereka pasti menyerap satu sama lain (dan kita memperbaikinya dengan distorsi ruang-waktu yang muncul yang dipicu oleh kedua galaksi).
Memang, distorsi ruang-waktu terkadang dapat diamati bahkan secara langsung - oleh lengkungan kasar gambar galaksi yang sangat jauh. Selain itu, distorsi ruang-waktu yang paling ekstrem yang kita ketahui dapat menyebabkan munculnya lubang hitam masif di luar angkasa: baru-baru ini kami berhasil mengamati bagaimana dua lubang tersebut saling menyerap dan membentuk yang lebih besar [Abbott et al., 2016]. Ada lubang hitam yang jutaan atau puluhan ribu juta kali lebih berat dari Matahari, sehingga lubang seperti itu dapat dengan mudah menelan seluruh tata surya. Namun demikian, monster-monster ini sangat kecil dibandingkan dengan galaksi itu sendiri, di tengah-tengahnya mereka ditemukan. Seringkali, lubang hitam seperti itu mengkhianati keberadaannya, menghasilkan dua berkas sinar berenergi tinggi.Balok-balok ini dikeluarkan dari lubang hitam ke arah yang berlawanan dari wilayah pusat kecil galaksi tempat lubang itu berada; partikel terbang dengan kecepatan yang dapat mencapai 99,5% dari kecepatan cahaya [Tombesi et al., 2012; Piner, 2006]. Suatu kali kami berhasil mengamati bagaimana sinar seperti itu terbang keluar dari satu galaksi dan mengarah ke galaksi lain, seolah-olah itu adalah perang antargalaksi kolosal.
Dalam skala yang lebih besar, seluruh wilayah ditemukan, diisi dengan sesuatu yang tak terlihat yang menembus ruang. Orang mendapat kesan bahwa zat yang sama sekali tidak dikenal ini menyumbang sekitar 84,5% dari semua materi di alam semesta. Pada saat yang sama, ada sesuatu yang lain yang mencapai batas terjauh dari Alam Semesta yang dapat diamati dan tampaknya memisahkannya ke arah yang berbeda dengan kecepatan yang meningkat. Seolah putus asa, para ilmuwan memberi kedua entitas ini nama yang agak samar - "materi gelap" dan "energi gelap", masing-masing. Materi gelap dan energi gelaplah yang pada dasarnya menentukan struktur keseluruhan alam semesta yang diketahui. Fakta berikut tampaknya lebih mengkhawatirkan: kosmologi modern hampir pasti membuktikan bahwa seluruh alam semesta yang kita kenal muncul dari satu ledakan raksasa,sebelumnya tidak ada sama sekali - jika kita bisa membicarakan sesuatu "sebelum" munculnya kontinum ruang-waktu, yang, seperti yang kita yakini, mendasari semua realitas material. Sungguh, konsep Big Bang seperti itu adalah ide yang fantastis!
Dan ada; tetapi kami memiliki semakin banyak bukti empiris yang mendukung fakta bahwa pada awal keberadaan, alam semesta kita memang luar biasa padat dan berkembang pesat. Itu tidak hanya berisi semua konten material dari kosmos yang kita ketahui, tetapi juga semua ruang-waktu, dengan latar belakang keberadaan realitas fisik sekarang dimainkan dan yang, tampaknya, membentang tanpa batas ke segala arah. Segala sesuatu yang kita ketahui tampaknya terjadi sebagai hasil dari Big Bang ini. Apa buktinya? Kita harus mengevaluasi kredibilitas ide ini dan mencoba memahami ke mana ia dapat membawa kita.
Dalam bab ini, kita akan membahas beberapa gagasan modern tentang asal-usul alam semesta itu sendiri, dan secara khusus kita akan menyentuh masalah berikut: sejauh mana ia dibenarkan untuk menggunakan fantasi untuk menjelaskan fakta empiris. Dalam beberapa tahun terakhir, berbagai eksperimen memang telah memberi kita sejumlah besar data yang secara langsung relevan untuk memahami asal mula alam semesta. Hal-hal yang sebelumnya tampak seperti kumpulan spekulasi yang sebagian besar belum teruji telah pindah ke kategori ilmu pasti. Yang paling penting untuk disebutkan adalah satelit COBE, diluncurkan pada 1989, WMAP, diluncurkan pada 2001, dan Observatorium Luar Angkasa. Papan yang telah beroperasi sejak 2009. Satelit yang disebutkan di atas secara bertahap mempelajari latar belakang gelombang mikro kosmik relik (lihat Bagian 3.4) secara lebih rinci. Namun, masalah yang belum terselesaikan tetap ada,dan untuk mencari jawabannya, beberapa spesialis dalam kosmologi teoretis pergi jauh ke dalam hutan, yang cukup tepat untuk menyebutnya sangat fantastis.
Ya, sampai taraf tertentu, fantasi memang dibenarkan, tetapi apakah para ahli teori modern tidak terburu-buru ke arah ini? Di bagian 4.3, saya akan menyuarakan versi saya yang agak tidak konvensional untuk memecahkan banyak misteri ini. Ide-ide yang melibatkan jawaban saya mungkin juga tampak liar bagi beberapa orang, dan saya akan menjelaskan secara singkat mengapa mereka harus dianggap serius. Namun demikian, dalam buku ini saya lebih tertarik pada gagasan yang saat ini mapan tentang tahap paling awal dari evolusi alam semesta kita yang indah, dan saya ingin membahas seberapa masuk akal arah tertentu yang digunakan oleh beberapa kosmolog modern untuk melakukan penelitian mereka.
Sebagai permulaan, kita memiliki teori relativitas umum Einstein yang agung, yang dikenal sangat akurat dalam menggambarkan struktur ruangwaktu lengkung kita dan gerakan benda-benda langit (lihat Bagian 1.1 dan 1.7). Pada tahun 1922 dan 1924, mengikuti upaya pertama Einstein untuk menerapkan teori ini untuk menggambarkan struktur integral Alam Semesta, ahli matematika Rusia Alexander Fridman pertama kali menemukan solusi untuk persamaan medan Einstein dalam konteks distribusi materi yang mengembang secara spasial homogen (homogen dan isotropik), dan cairan ideal dianggap sebagai model perkiraan materi tersebut. (solusi debu) mewakili distribusi massa-energi rata-rata galaksi [Rindler, 2001; Wald, 1984; Hartle, 2003; Weinberg, 1972]. Memang, dari sudut pandang empiris, tampaknyabahwa dalam hal ini diperoleh pendekatan umum yang cukup baik untuk distribusi rata-rata materi di alam semesta yang ada, dan tensor energinya diturunkanT , yang dibutuhkan Friedman untuk merepresentasikan gravitasi dalam persamaan Einstein G = 8π ע T + Λg (lihat Bagian 1.1). Ciri khas model Friedman adalah ekspansi dimulai dengan singularitas (sekarang disebut Big Bang). Kemudian kelengkungan ruang-waktu menjadi tak terhingga, dan kerapatan massa-energi dari sumber materi T akan melonjak hingga tak terhingga jika kita mencoba memundurkan waktu kembali ke singularitas ruang-waktu ini.
(Anehnya, istilah "Ledakan Besar" yang sekarang umum digunakan dianggap merendahkan; istilah ini diciptakan oleh Fred Hoyle, seorang pendukung setia teori alternatif alam semesta diam; lihat bagian 3.2.) Dia pertama kali menyebut kata "Ledakan Besar" di radio BBC dibuat tahun 1950. Bagian 3.10 menyebutkan wawancara ini dalam konteks yang berbeda; kemudian, sebuah buku disusun atas dasar mereka [Hoyle, 1950].
Sementara saya akan mengasumsikan secara kondisional bahwa konstanta kosmologis Einstein yang sangat kecil Λ - konstanta inilah yang menentukan percepatan ekspansi Alam Semesta, yang disebutkan sebelumnya (lihat juga Bagian 1.1) - sama dengan nol. Maka kita perlu mempertimbangkan hanya tiga situasi terpisah yang ditentukan oleh geometri spasial: kelengkungan ruang K bisa positif (K> 0), nol (K = 0) atau negatif (K <0). Dalam buku-buku otoritatif tentang kosmologi, merupakan kebiasaan untuk menormalkan nilai K, membawanya ke salah satu dari tiga nilai: 1, 0, –1. Di sini ceritanya akan lebih jelas jika kita menganggap K sebagai bilangan real yang mencirikan kelengkungan ruang yang sebenarnya. Kita dapat menganggap K sebagai kuantitas yang menunjukkan kelengkungan spasial pada waktu tertentu t yang dipilih. Misalnya, Anda setujubahwa t akan sesuai dengan masa hamburan terakhir (lihat Bagian 3.4), ketika latar belakang gelombang mikro kosmik terbentuk, tetapi pemilihan momen tertentu tidak penting dalam kasus ini. Intinya adalah bahwa tanda K tidak akan berubah seiring waktu, oleh karena itu, nilai K positif, negatif atau nol mencirikan model secara keseluruhan, terlepas dari "titik referensi" yang dipilih.
Namun, perlu dicatat bahwa nilai K itu sendiri tidak sepenuhnya mencirikan geometri ruang-waktu. Ada juga versi "lipat" non-standar dari model tersebut, yang geometri spasialnya cukup kompleks, dan dalam beberapa contoh, Alam Semesta mungkin terbatas, bahkan jika K = 0 atau K <0. Beberapa ilmuwan tertarik pada
model seperti itu (lihat Levin [2012], Luminet et al., [2003], aslinya Schwarzschild [1900]). Namun, model ini tidak penting bagi kami di sini; masalah ini tidak secara signifikan mempengaruhi sebagian besar argumen yang saya sampaikan dalam kasus ini. Jika kita tidak memperhitungkan komplikasi topologi, maka kita hanya mendapatkan tiga jenis geometri homogen, yang (pada bidang) digambarkan dengan sangat indah oleh seniman Belanda M.C. Escher (Gambar 3.1; bandingkan juga dengan Gambar 1.38 di bagian 1.15). Gambar 3D terlihat sama.
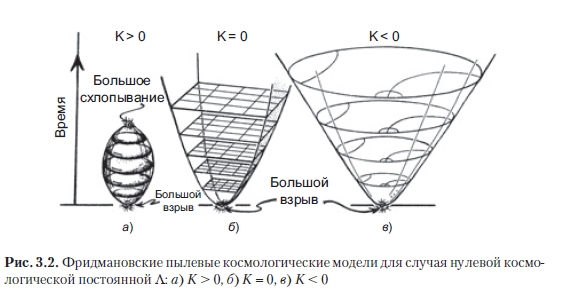
Cara termudah untuk memahami kasus ini adalah K = 0, karena dalam kasus ini penampang spasial akan menjadi ruang Euclidean tiga dimensi biasa, meskipun untuk menggambarkan alam semesta yang mengembang, kita membutuhkan banyak bagian yang berurutan: lihat Gambar. 3.2 b. (Perluasan ini dapat dipahami dalam istilah garis mirip waktu divergen yang sesuai dengan garis dunia dari galaksi ideal yang dijelaskan oleh model ini. Ini akan menjadi garis waktu, yang akan kita bicarakan nanti.) Ruang tiga dimensi, yang merupakan bagian spasial dalam kasus K> 0, sedikit lebih sulit untuk direpresentasikan. karena mereka adalah 3-bola ( ), yang masing-masing dalam tiga dimensi mirip dengan permukaan dua dimensi dari bola biasa (), dan perluasan alam semesta dinyatakan sebagai peningkatan jari-jari bola seiring waktu (Gambar 3.2 a). Dalam kasus kelengkungan negatif (K <0), ruang tiga dimensi memiliki geometri hiperbolik (alias geometri Lobachevsky). Geometri seperti itu dapat direpresentasikan secara akurat menggunakan representasi konformal (Beltrami - Poincaré), yang dalam kasus dua dimensi digambarkan sebagai daerah yang dibatasi oleh lingkaran S dalam bidang Euclidean, di mana garis lurus direpresentasikan sebagai busur melingkar yang memotong lingkaran pembatas pada sudut siku-siku (Gbr. 3.2 di dan Gambar 1.38 di bagian 1.15) (lihat, khususnya, RQR, bagian 2.4-2.6; Needham [1997]). Geometri hiperbolik tiga dimensi terlihat serupa, namun, alih-alih lingkaran S, ia berisi sebuah bola (bola 2 biasa), yang membatasi suatu daerah (bola 3) di ruang tiga dimensi Euclidean.
Istilah "konformal" yang digunakan dalam model ini digunakan karena dalam geometri hiperbolik, sudut antara dua kurva mulus di titik perpotongannya akan sama seperti di latar belakang geometri Euclidean (misalnya, sudut di ujung sirip ikan pada Gambar. 1.38a atau sayap-sayap iblis pada Gambar 3.1c ditampilkan tanpa distorsi, tidak peduli seberapa dekat mereka dengan lingkaran pembatas). Rumusan lain (kasar) dari prinsip yang sama adalah sebagai berikut: bentuk (tetapi bukan dimensi) dari detail yang sangat halus dalam representasi seperti itu selalu ditampilkan tanpa distorsi (lihat juga Gambar A.39 di Bagian A.10).
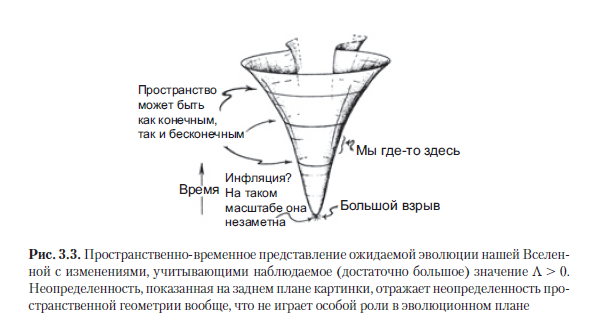
Seperti disebutkan sebelumnya, beberapa bukti meyakinkan telah ditemukan bahwa di alam semesta kita konstanta kosmologis Λ memiliki nilai positif yang kecil, jadi kita harus mempertimbangkan model Friedmann yang sesuai dengan Λ> 0. Faktanya, tidak peduli betapa tidak signifikannya Λ, nilainya masih cukup besar (pada saat yang sama, menurut persamaan Einstein, kami terus menganggapnya sebagai konstanta) untuk mengatasi keruntuhan dan "keruntuhan besar" yang ditunjukkan pada Gambar. 3.2 a. Sebaliknya, dengan ketiga kemungkinan nilai K yang diizinkan oleh pengamatan saat ini, alam semesta pada akhirnya akan mengembang dengan percepatan. Dengan konstanta positif Λ, perluasan alam semesta akan terus berlanjut tanpa batas dan akhirnya menjadi eksponensial (lihat Gambar A.1 di Bagian A.1).Menurut perhitungan seperti itu, kita membayangkan sejarah umum alam semesta seperti yang ditunjukkan pada Gambar. 3.3. Latar belakang digambarkan secara samar-samar untuk menunjukkan bahwa pengamatan memungkinkan ketiga variasi dalam kelengkungan spasial K.
Varian masa depan jauh dalam semua model ini untuk Λ> 0, meskipun terdapat beberapa ketidakteraturan di dalamnya, sangat mirip dan dijelaskan dengan baik oleh model ruang-waktu tertentu, yang disebut ruang de Sitter. Tensor Einstein di dalamnya adalah Λg . Model ini ditemukan oleh Willem de Sitter (dan secara independen oleh Tullio Levi-Civita) pada tahun 1917 (lihat [de Sitter, 1917a, b; Levi-Cività, 1917; Schrödinger, 1956]; PKR, hal. 28.4). Saat ini, secara umum diterima bahwa model ini mendekati masa depan jauh alam semesta kita, ketika tensor energi sepenuhnya ditentukan oleh Λ, oleh karena itu, di masa yang sangat jauh, situasi G≈Λg akan berkembang .
Tentu saja, di sini kita mengasumsikan bahwa persamaan Einstein (G = 8π ע T + Λg)akan bertindak tanpa batas dan nilai Λ, yang ditentukan di zaman kita, akan tetap konstan. Dalam Bagian 3.9, akan diperlihatkan bahwa, menurut ide eksotis kosmologi inflasi, model de Sitter seharusnya menggambarkan alam semesta pada tahap yang jauh lebih awal, segera setelah Big Bang, tetapi nilai time pada saat itu seharusnya sangat tinggi daripada yang sekarang. Pertanyaan-pertanyaan ini akan menjadi penting bagi kita nanti (lihat bagian 3.7-3.9 dan 4.3), tetapi untuk saat ini kita tidak akan membahasnya secara rinci.
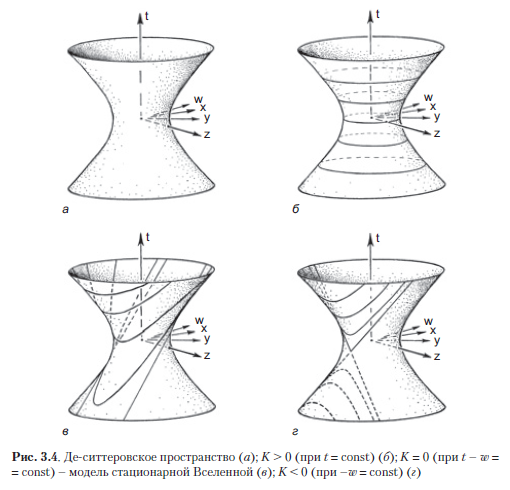
Ruang De Sitter adalah ruangwaktu sangat simetris yang dapat digambarkan sebagai bola (pseudo-) dalam ruang Minkowski lima dimensi (Gambar 3.4 a). Bola (semu) ini muncul di titik = –3 / Λ, memperoleh struktur metrik lokal dari ruang Minkowski lima dimensi terlampir dengan koordinat (t, w, x, y, z) (Mereka yang tahu bagaimana standar metrik ditulis menggunakan diferensial, orang memahami bahwa metrik Minkowski lima dimensi ini mengambil bentuk =.) Ruang De-Sitter sepenuhnya mengulangi kesimetrian ruang Minkowski empat dimensi; dalam kedua kasus, kami memiliki grup simetri 10 parameter. Anda juga dapat mengingat ruang hipotetis anti-de-Sitter yang dibahas di bagian 1.15. Ini sangat erat kaitannya dengan ruang de Sitter dan memiliki kelompok simetri dengan urutan yang sama.
Ruang De Sitter merupakan model kosong dengan tensor energi Tadalah nol, jadi tidak ada galaksi (ideal) yang dapat menentukan garis waktu, yang bagian spasial tiga dimensi ortogonalnya memungkinkan seseorang untuk menentukan geometri tiga dimensi tertentu dari "waktu sinkron". Faktanya, fakta yang cukup luar biasa: ternyata bagian spasial tiga dimensi tersebut (dengan waktu sinkron) dapat dipilih di ruang de Sitter dengan tiga cara yang berbeda secara fundamental, sehingga ruang de Sitter dapat diartikan sebagai Semesta yang mengembang secara seragam di ruang angkasa dengan masing-masing dari tiga alternatif. jenis kelengkungan spasial, tergantung pada bagaimana ia dipotong oleh bagian tiga dimensi yang sesuai dengan waktu kosmik yang sama: K> 0 (pada t = konst), K = 0 (pada t - w = konst) dan K <0 ( di –w = const) (Gbr. 3.4 b - d).Hal ini dengan indah ditunjukkan oleh Erwin Schrödinger dalam bukunya Expanding Universes (1956). Model sebelumnya dari alam semesta stasioner, yang akan kita bahas di Bagian 3.2, dijelaskan oleh ruang de Sitter sesuai dengan penampang K = 0 yang ditunjukkan pada Gambar. 3.4 c (dan sesuai disajikan pada Gambar. 3.26 b di bagian 3.5). Sebagian besar versi kosmologi inflasi (yang akan kita bahas di Bagian 3.9) juga menggunakan potongan seperti itu K = 0, sehingga inflasi dapat berlanjut secara seragam dan eksponensial untuk waktu yang tidak terbatas.26 b dalam Bagian 3.5). Sebagian besar versi kosmologi inflasi (yang akan kita bahas di Bagian 3.9) juga menggunakan potongan K = 0, sehingga inflasi dapat berlanjut secara seragam dan eksponensial untuk waktu yang tidak terbatas.26 b dalam Bagian 3.5). Sebagian besar versi kosmologi inflasi (yang akan kita bahas di Bagian 3.9) juga menggunakan potongan seperti itu K = 0, sehingga inflasi dapat berlanjut secara seragam dan eksponensial untuk waktu yang tidak terbatas.
Faktanya, sehubungan dengan struktur skala besar dari Alam Semesta kita yang sebenarnya, pengamatan modern tidak memungkinkan kita untuk menjawab secara tegas varian mana dari varian geometri spasial ini yang paling tepat menggambarkannya. Namun demikian, apa pun jawaban akhirnya, tampaknya opsi K = 0 sekarang tidak terlalu mendekati kebenaran (patut dicatat, terutama mengingat bukti yang tampaknya meyakinkan yang mendukung K <0 yang muncul menjelang akhir abad ke-20). Sedikit banyak, situasi ini sangat tidak memuaskan dari sudut pandang empiris; karena jika kita hanya dapat mengatakan bahwa nilai K sangat mendekati nol, maka masih ada kemungkinan bahwa pengamatan yang lebih cermat (atau teori yang lebih meyakinkan) selanjutnya akan menunjukkan bahwabahwa Semesta kita lebih tepat bersesuaian dengan beberapa geometri spasial lainnya (yaitu, sferis atau hiperbolik). Jadi, jika pada akhirnya ada bukti bagus yang mendukung K> 0, ini akan menjadi sangat penting dari sudut pandang filosofis, karena ini berarti bahwa dimensi spasial alam semesta terbatas. Akan tetapi, untuk saat ini, adalah kebiasaan untuk menyatakan hal-hal berikut: menurut pengamatan, K = 0. Ini mungkin merupakan perkiraan yang sangat baik, tetapi bagaimanapun juga kita tidak tahu seberapa dekat alam semesta nyata dengan homogenitas dan isotropi spasial yang sebenarnya, terutama dengan adanya data yang saling bertentangan. diperoleh dengan mengamati latar belakang gelombang mikro kosmik (misalnya, [Starkman et al., 2012; Gurzadyan dan Penrose, 2013, 2016]).Jika pada akhirnya ada bukti bagus yang mendukung K> 0, ini akan menjadi sangat penting dari sudut pandang filosofis, karena ini berarti bahwa dimensi spasial alam semesta terbatas. Akan tetapi, untuk saat ini, adalah kebiasaan untuk menyatakan hal-hal berikut: menurut pengamatan, K = 0. Ini mungkin merupakan perkiraan yang sangat baik, tetapi bagaimanapun juga kita tidak tahu seberapa dekat alam semesta nyata dengan homogenitas dan isotropi spasial yang sebenarnya, terutama dengan adanya data yang saling bertentangan. diperoleh dengan mengamati latar belakang gelombang mikro kosmik (misalnya, [Starkman et al., 2012; Gurzadyan dan Penrose, 2013, 2016]).jika pada akhirnya ada bukti bagus yang mendukung K> 0, ini akan menjadi sangat penting dari sudut pandang filosofis, karena itu berarti bahwa dimensi spasial alam semesta terbatas. Akan tetapi, untuk saat ini, adalah kebiasaan untuk menyatakan hal-hal berikut: menurut pengamatan, K = 0. Ini mungkin merupakan perkiraan yang sangat baik, tetapi bagaimanapun juga kita tidak tahu seberapa dekat alam semesta nyata dengan homogenitas spasial dan isotropi yang sebenarnya, terutama mengingat data konflik tertentu. diperoleh dengan mengamati latar belakang gelombang mikro kosmik (misalnya, [Starkman et al., 2012; Gurzadyan dan Penrose, 2013, 2016]).Akan tetapi, pada saat ini, adalah kebiasaan untuk menyatakan hal-hal berikut: menurut pengamatan, K = 0. Ini mungkin merupakan perkiraan yang sangat baik, tetapi dalam hal apapun kita tidak tahu seberapa dekat alam semesta nyata dengan homogenitas dan isotropi spasial yang sebenarnya, terutama dengan adanya data konflik tertentu. diperoleh dengan mengamati latar belakang gelombang mikro kosmik (misalnya, [Starkman et al., 2012; Gurzadyan dan Penrose, 2013, 2016]).Akan tetapi, untuk saat ini, adalah kebiasaan untuk menyatakan hal-hal berikut: menurut pengamatan, K = 0. Ini mungkin merupakan perkiraan yang sangat baik, tetapi bagaimanapun juga, kita tidak tahu seberapa dekat alam semesta nyata dengan homogenitas dan isotropi spasial yang sebenarnya, terutama mengingat data konflik tertentu. diperoleh dengan mengamati latar belakang gelombang mikro kosmik (misalnya, [Starkman et al., 2012; Gurzadyan dan Penrose, 2013, 2016]).
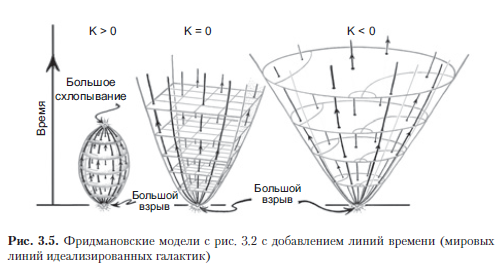
Untuk membangun gambaran ruang-waktu lengkap sesuai dengan model Friedmann dan generalisasinya, Anda perlu mengetahui bagaimana "dimensi" geometri spasial kita akan berubah dari waktu ke waktu, dan sejak awal. Dalam model kosmologi standar, misalnya oleh Friedman, atau dalam model umum, secara singkat disebut FLRU (Friedman - Lemaitre - Robertson - Walker), dalam semua model kelas umum ini bagian spasial homogen dan isotropik dan total ruang-waktu memiliki kesimetrian yang sama dengan dan bagian itu sendiri. Mereka memiliki definisi yang jelas tentang waktu kosmik t, yang menggambarkan evolusi model universal semacam itu. Waktu kosmik ini dimulai pada saat t = 0 (Big Bang) dan dihitung dengan jam ideal mengikuti garis dunia galaksi ideal (Gbr. 3.5, serta Gbr. 1.17 di bagian 1.7). Saya akan merujuk pada garis dunia ini sebagai garis waktu dalam model FLRU (dalam karya kosmologis kadang-kadang disebut garis dunia pengamat fundamental). Garis waktu adalah kurva geodesik ortogonal ke bagian spasial, yang pada gilirannya merupakan bidang-3 dengan nilai t yang sama.
Kasus ruang de Sitter memiliki ciri penting: karena, seperti disebutkan sebelumnya, ruang kosong, yaitu, tensor momentum-energi T dalam persamaan G = 8πT + Λg sama dengan nol, maka kita tidak memiliki garis dunia apa pun yang terkait dengan benda material, yang memungkinkan akan kita mendefinisikan garis waktu atau, masing-masing, geometri spasial. Oleh karena itu, secara lokal kami memiliki pilihan bagaimana menafsirkan model penggambaran Alam Semesta ini: apakah itu sesuai dengan K> 0, K = 0, atau K <0. Namun demikian, secara global, ketiga situasi ini berbeda, seperti yang dapat dilihat pada Gambar. 3.4 b - d: dalam masing-masing kasus ini, pemotongan menangkap bagian berbeda dari ruang de-Sitter integral. Lebih lanjut
Saya akan melanjutkan dari fakta bahwa T tidak sama dengan nol dan memberikan kerapatan energi positif dari materi, yang memungkinkan untuk menentukan dengan baik garis waktu dan 3-permukaan seperti ruang waktu konstan untuk setiap nilai t, seperti yang ditunjukkan pada Gambar. 3.2.
Dalam kasus dengan kelengkungan ruang yang positif (K> 0) di alam semesta Friedman standar yang dipenuhi dengan debu, seseorang dapat mengkarakterisasi “ukurannya” dengan menggunakan jari-jari R dari 3 bagian spasial bola, dan mempelajari ukuran ini sebagai fungsi dari t. Pada Λ = 0, kita menemukan fungsi R (t) yang mendeskripsikan sikloid dalam bidang (R, t) (dalam hal ini, kecepatan cahaya diambil sebagai satu unit: c = 1). Sikloid adalah kurva dengan karakteristik geometris sederhana: ia digambarkan dengan sebuah titik lingkaran yang bergulung di sepanjang sumbu-t (Gambar 3.6 b). Perhatikan bahwa (setelah waktu) nilai R kembali mencapai nol, seperti dalam Big Bang, oleh karena itu seluruh model Alam Semesta dengan 0 <t < runtuh lagi menjadi singularitas, dan momen ini sering disebut keruntuhan besar.
Dalam kasus lainnya K <0 dan K = 0 (dengan nol Λ), alam semesta akan mengembang tanpa batas dan tidak akan ada keruntuhan besar. Dalam kasus K <0, ada "jari-jari" yang mirip dengan R, tetapi untuk K = 0, Anda cukup memilih pasangan sembarang garis dunia dari galaksi ideal dan menganggap R segmen yang membaginya dalam ruang. Dalam kasus K = 0, tingkat ekspansi cenderung asimtotik ke nol, dan dalam kasus K <0 - ke beberapa nilai positif.
Pengamatan modern menunjukkan bahwa Λ kemungkinan besar positif dan nilainya cukup untuk memainkan peran yang menentukan dalam laju perluasan Alam Semesta, oleh karena itu nilai K kehilangan kepentingannya untuk dinamika ini, dan Semesta akhirnya terurai menjadi ekspansi yang dipercepat, seperti yang ditunjukkan di ara. 3.3.
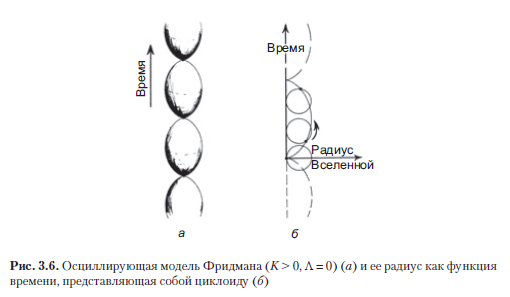
Pada permulaan kosmologi relativistik, model dengan nilai K positif (dan Λ = 0) sering disebut sebagai model berosilasi (Gambar 3.6 a), karena kurva sikloid akan terus berlanjut tanpa batas jika kita membiarkan "lingkaran" membuat lebih dari satu putaran (kurva putus-putus pada Gambar 3.6 b ). Dapat diasumsikan bahwa bagian-bagian sikloid yang terus-menerus diganti mungkin sesuai dengan siklus-siklus yang berurutan dalam sejarah Alam Semesta yang sebenarnya, di mana, di bawah pengaruh guncangan tertentu, setiap keruntuhan yang dialami Alam Semesta akan digantikan oleh Ledakan Besar baru. Kemungkinan serupa juga muncul pada K = 0, dan dapat diasumsikan bahwa pada tahap sebelumnya, ruang-waktu mengalami keruntuhan, identik dengan pembalikan waktu selama tahap ekspansi, dan Ledakan Besar tahap tersebut bertepatan dengan Big Bang, yang kita anggap sebagai awal dari perluasan Alam Semesta saat ini.Sekali lagi, orang harus membayangkan semacam pantulan yang entah bagaimana mengubah ledakan menjadi perpanjangan.
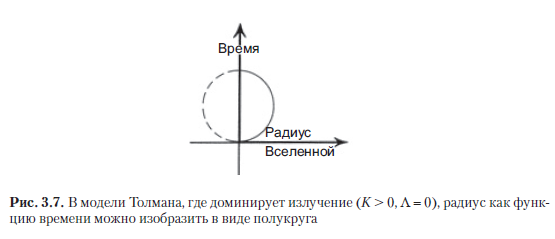
Namun, agar gambar seperti itu menjadi masuk akal secara fisik, diperlukan beberapa skema matematika yang meyakinkan yang akan sesuai dengan konsep dan metode fisik modern dan di mana rebound tersebut akan cocok. Misalnya, Anda dapat mengubah persamaan keadaan yang diadopsi oleh Friedman, yang dengannya dia mencoba menjelaskan distribusi umum materi dalam galaksi yang "tercoreng merata". Friedman menggunakan model perkiraan yang kadang disebut model debu; model ini tidak memperhitungkan interaksi apa pun (kecuali gravitasi) antara "elemen penyusun" (yaitu, "galaksi"), yang garis dunianya adalah garis waktu. Jika kita mengubah persamaan keadaan, ini secara signifikan dapat mempengaruhi sifat R (t) dekat t = 0. Pendekatan yang lebih akurat,daripada debu Friedman (dalam periode segera setelah Big Bang), persamaan keadaan seperti itu muncul, yang kemudian digunakan oleh Richard Chase Tolman [1934], seorang spesialis Amerika dalam fisika matematika dan kosmologi. Dalam model FLRU Tolman, persamaan keadaan radiasi murni digunakan. Dipercaya bahwa ia mendekati dengan baik keadaan materi pada tahap paling awal perkembangan Alam Semesta, ketika suhunya sangat panas sehingga setiap partikel memiliki energi yang jauh lebih banyak daripada menurut persamaan.bahwa ia mendekati dengan baik keadaan materi pada tahap paling awal perkembangan Alam Semesta, ketika suhunya sangat panas sehingga setiap partikel memiliki energi yang jauh lebih banyak daripada menurut persamaanbahwa ia mendekati dengan baik keadaan materi pada tahap paling awal perkembangan Alam Semesta, ketika suhunya sangat panas sehingga setiap partikel memiliki energi yang jauh lebih banyak daripada menurut persamaanuntuk massa m bahkan dari partikel terberat yang bisa ada segera setelah Big Bang. Dalam skema Tolman untuk kasus K> 0, kurva R (t) bukanlah busur sikloid, tetapi (dengan skala R dan t yang dipilih dengan tepat) membentuk setengah lingkaran (Gbr. 3.7). Dalam kasus model debu, seseorang dapat membenarkan transisi dari Runtuh ke Ledakan dengan menggunakan kelanjutan analitik (lihat Bagian A.10), yang memang memungkinkan seseorang untuk berpindah dari satu busur kurva sikloid ke busur berikutnya menggunakan metode matematika seperti itu. Tetapi dalam model Tolman dengan radiasi murni, kelanjutan analitik hanya akan melengkapi setengah lingkaran dan mengubahnya menjadi lingkaran, dan ini tidak masuk akal jika prosedur ini menarik bagi kami untuk menggambarkan pantulan, yaitu, harus memungkinkan kelanjutan menuju nilai negatif t.
Agar persamaan keadaan baru dapat mendeskripsikan mekanisme pantulan, diperlukan sesuatu yang jauh lebih radikal daripada radiasi Tolman. Dalam hal ini, hal yang serius perlu diperhatikan: jika rebound terjadi pada beberapa transisi nonsingular, di mana kehalusan ruang-waktu dan simetri spasial model dipertahankan, maka garis waktu konvergen dari fase kompresi dapat berubah menjadi garis waktu yang berbeda dari fase ekspansi, melewati bottleneck Itu akan menggabungkan kedua fase ini. Jika leher ini mulus (nonsingular), maka transformasi dari konvergensi garis waktu yang ekstrim menjadi divergensi yang ekstrim akan dapat dicapai dengan kelengkungan leher yang luar biasa, yang akan menyebabkan tolakan yang kuat, dan ini sangat bertentangan dengan kondisi standar untuk energi positif,yang dipenuhi oleh materi klasik biasa (lihat bagian 1.11, 3.2 dan 3.7; [Hawking dan Penrose, 1970]).
Oleh karena itu, seseorang tidak dapat mengharapkan bahwa persamaan klasik keadaan yang masuk akal akan memungkinkan kita untuk mendeskripsikan rebound dalam konteks model FLRU, dan pertanyaan yang tak terelakkan muncul: bukankah persamaan mekanika kuantum membantu kita bergerak ke arah ini? Perlu diperhatikan bahwa di dekat singularitas FLRU klasik, kelengkungan ruang-waktu menjadi besar tanpa batas. Jika kita mencoba mendeskripsikan kelengkungan seperti itu dalam kaitannya dengan jari-jarinya, maka jari-jari ini (kebalikan dari kelengkungan) akan menjadi kecil. Melanjutkan untuk mematuhi konsep geometri klasik, ketika kita mendekati singularitas klasik, kita akan menerima jari-jari kelengkungan ruang-waktu yang semakin kecil, dan sebagai akibatnya, jari-jari akan menjadi lebih kecil daripada skala Planck dari urutan
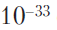lihat (lihat bagian 1.1 dan 1.5). Kebanyakan ahli teori, memikirkan tentang gravitasi quantum, berasumsi bahwa pada skala seperti itu, ruangwaktu sudah sangat berbeda dari bentuk biasanya (lipatan halus) (walaupun dalam Bagian 4.3 saya akan mengemukakan argumen yang sama sekali berbeda tentang skor ini). Benar atau tidak, tidak ada alasan untuk meragukan bahwa prosedur relativitas umum pasti harus dimodifikasi sehingga digabungkan dengan metode mekanika kuantum pada pendekatan geometri ruang-waktu yang melengkung secara radikal. Artinya, kita memerlukan teori gravitasi kuantum yang sesuai untuk kasus kita, yang memungkinkan kita mengatasi situasi di mana prosedur Einstein klasik mengarah pada singularitas (tetapi bandingkan dengan Bagian 4.3).
Kita sering mendengar pernyataan bahwa preseden seperti itu sudah terjadi. Seperti dicatat di Bagian 2.1, pada awal abad ke-20, masalah serius muncul dengan konsep klasik atom, karena, menurut teori, atom seharusnya runtuh secara serempak ke dalam keadaan tunggal, ketika elektron secara spiral jatuh ke inti (dengan pembentukan pulsa radiasi), dan menyelesaikannya. masalah ini hanya mungkin terjadi dengan munculnya mekanika kuantum. Tidakkah seharusnya orang berharap bahwa bahkan ketika membahas kehancuran dahsyat seluruh Alam Semesta, situasinya bisa menjadi lebih jelas di tingkat mekanika kuantum? Tapi inilah tangkapannya: bahkan sekarang, tidak ada hipotesis gravitasi quantum yang diterima secara umum. Yang lebih serius adalah kenyataan bahwa sebagian besar hipotesis yang telah dikemukakan tidak menyelesaikan masalah singularitas - singularitas tetap ada bahkan dalam teori terkuantisasi.Ada beberapa pengecualian penting - hipotesis pantulan kuantum nonsingular [Bojowald, 2007; Ashtekar et al., 2006], tetapi saya harus kembali ke topik ini di Bagian 3.9 dan 3.11 (serta di Bagian 4.3), di mana saya berpendapat bahwa hipotesis semacam itu tidak benar-benar memberikan banyak harapan untuk memecahkan masalah singularitas di Alam Semesta kita. ...
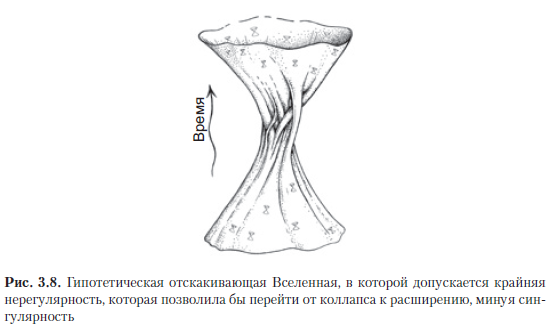
Kemungkinan yang sama sekali berbeda untuk menghindari singularitas dikaitkan dengan ekspektasi bahwa penyimpangan kecil dari simetri yang tepat yang ada pada tahap keruntuhan Semesta dapat tumbuh secara radikal saat Ledakan Besar mendekat, oleh karena itu, segera sebelum keruntuhan total, struktur ruang-waktu tidak akan benar-benar sesuai dengan model FLRU. Oleh karena itu, harapan sering disuarakan bahwa singularitas yang memanifestasikan dirinya dalam model-model FLRU mungkin salah dan bahwa dalam situasi asimetris yang lebih umum, singularitas ruang-waktu klasik tidak akan muncul; oleh karena itu, ada alasan untuk memperkirakan bahwa, dalam kasus umum, alam semesta yang runtuh, karena beberapa geometri ruang-waktu menengah yang kompleks (Gbr. 3.8), dapat berubah menjadi ekspansi tak beraturan.Bahkan Einstein sendiri mencoba mengemukakan argumen seperti itu - bahwa singularitas dapat dihindari dengan memantul dari keruntuhan yang tidak teratur [Einstein, 1931; Einstein dan Rosen, 1935] atau karena keruntuhan terakhir dan singularitas entah bagaimana dapat mencegah gerakan orbital benda-benda langit [Einstein, 1939].
Dapat dikatakan bahwa setelah keruntuhan yang hampir tunggal (tetapi tidak sepenuhnya tunggal), suatu keadaan akan muncul, gangguan yang secara bertahap akan menghilang, dan sebagai akibatnya akan sangat mirip dengan model FLRU yang berkembang (seperti pada Gambar 3.8). Pada tahun 1963, masalah ini dianalisis secara rinci oleh dua fisikawan teoretis Soviet - Evgeny Mikhailovich Lifshits dan Isaak Markovich Khalatnikov [Lifshits dan Khalatnikov, 1963]. Pekerjaan mereka menunjukkan bahwa, dalam kondisi normal, singularitas seperti itu tampaknya tidak muncul, yang mendukung hipotesis pantulan non-singular yang dijelaskan di atas. Dengan demikian, dikatakan bahwa dalam relativitas umum, singularitas ruang-waktu yang muncul selama keruntuhan gravitasi dan muncul dalam solusi pasti yang diketahui dari model Friedmann yang runtuh atau model FLRU lainnya dihasilkan hanya karenabahwa solusi yang diketahui memiliki sifat spesifik yang tidak realistis, misalnya, simetri yang ketat. Oleh karena itu, singularitas seperti itu tidak akan berkembang dalam kondisi gangguan asimetris yang khas. Namun, asumsi ini belum dikonfirmasi, yang akan dibahas pada bagian selanjutnya.
»Rincian lebih lanjut tentang buku dapat ditemukan di situs web penerbit
» Daftar Isi
» Kutipan
Untuk Habitants diskon 30% untuk kupon - Penrose
Setelah pembayaran untuk versi kertas dari buku tersebut, sebuah e-book dikirim ke email.