Hore!
Tim anak sekolah Rusia menempati posisi kedua!
Medali emas diraih oleh Danila Demin dari Sochi (36 poin) dan Alexey Lvov dari Novosibirsk (36 poin). Perak diambil oleh Ivan Gaidai-Turlov (25), Anton Sadovnichy (29) dari Moskow, Danil Sibgatullin (29) dari Moskow dan Kazan, dan Maxim Turevsky (30) dari St. Petersburg.
Pemenang mutlak Olimpiade dalam kompetisi individu adalah seorang anak sekolah dari China Jinmin Li, yang mencetak sebanyak mungkin 42 poin.
Saya baru-baru ini menerbitkan teks masalah dan beberapa di antaranya diselesaikan oleh pembaca Habr di komentar.
Di bawah pemotongan adalah beberapa statistik menarik tentang hasil Olimpiade .

Teman-teman kita!
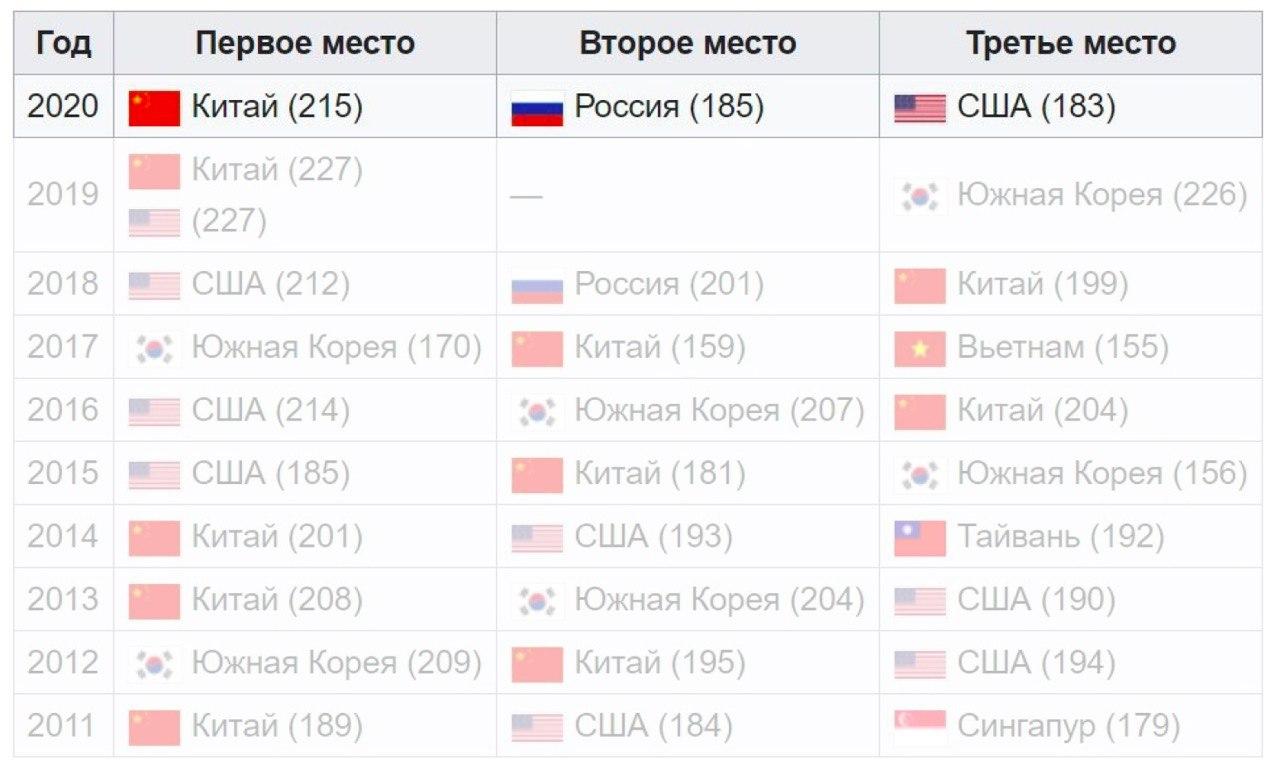
Hasil Tim

China memimpin. Selisih antara Rusia dan Amerika Serikat adalah 2 poin.

Sangat menarik bahwa Amerika Serikat memiliki seorang pemimpin dengan nama keluarga Asia yang diucapkan, dan wakilnya. pemimpin - dengan nama dan nama keluarga Ukraina yang diucapkan.
Hasil individu


Peserta Cina (1, 2, 3) dengan selisih lebar. Perwakilan dari banyak negara mencetak 36 poin (tempat ke-4).

Juara mutlak Jinmin Li dari Chongqing. Menghormati.
Tugas

- PDF dengan tugas dalam bahasa Inggris
- PDF dengan tugas dalam bahasa Rusia
Masalah 1
Di dalam ABCD segiempat cembung, ada titik P sehingga persamaan
equalPAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC tahan.
Buktikan bahwa tiga garis lurus berikut berpotongan pada satu titik: bisectors dalam dari sudut ∠ADP dan ∠PCB dan titik tengah tegak lurus dengan segmen AB.
Masalah 2
Diberikan bilangan real a, b, c, d sehingga a> b> c> d> 0 dan a + b + c + d = 1.
Buktikan bahwa
(a + 2b + 3c + 4d) a a b b c c d d <1.
Solusi darinovoselov sini
Masalah 3
Ada 4n kerikil dengan massa 1, 2, 3, ..., 4n . Masing-masing kerikil diwarnai salah satu dari n warna, dan ada 4 kerikil di setiap warna.
Buktikan bahwa kerikil dapat dibagi menjadi dua tumpukan dengan berat total yang sama sehingga setiap tumpukan berisi dua kerikil dengan warna masing-masing.
Keputusan daricelen di sini
Keputusan darinovoselov sini
Masalah 4
Sebuah bilangan bulat n> 1 diberikan . Ada n 2 stasiun digerakkan di lereng gunung pada ketinggian yang berbeda. Masing-masing dari dua perusahaan yang digerakkan oleh kabel A dan B memiliki lift k . Setiap lift melakukan transfer langsung reguler dari salah satu stasiun ke stasiun lain yang lebih tinggi. K transfer perusahaan A dimulai di k stasiun berbeda; mereka juga berakhir di k stasiun berbeda; dengan transfer yang dimulai di atas dan berakhir di atas. Kondisi yang sama terpenuhi untuk perusahaan B. Kami akan mengatakan bahwa dua stasiun terhubungperusahaan yang digerakkan oleh kabel, jika Anda dapat pergi dari stasiun bawah ke atas menggunakan satu atau lebih transfer perusahaan ini (transfer lain antar stasiun dilarang). Temukan k terkecil yang diketahui ada dua stasiun yang dihubungkan oleh kedua perusahaan.
Masalah 5
Terdapat n> 1 kartu yang masing-masing berisi bilangan bulat positif.
Ternyata untuk dua kartu mana saja, rata-rata aritmatika dari angka-angka yang tertulis di atasnya sama dengan rata-rata geometris dari angka-angka yang tertulis pada kartu-kartu dari rangkaian tertentu yang terdiri dari satu atau lebih kartu. Untuk n manakah itu berarti semua angka yang tertulis di kartu sama?
Keputusan darinovoselov sini
Masalah 6
Buktikan bahwa terdapat konstanta positif c yang dipegang pernyataan berikut:
Misalkan S adalah himpunan n> 1 titik bidang di mana jarak antara dua titik paling sedikit 1. Kemudian ada garis ℓ yang memisahkan himpunan S sedemikian rupa sehingga jarak dari salah satu titik S ke ℓ setidaknya adalah cn −1/3 .
(Garis lurus ℓ memisahkan himpunan titik S jika memotong beberapa segmen yang ujungnya dimiliki S.)
Keterangan. Hasil yang lebih lemah dengan cn −1/3 diganti dengan cn −α dapat diperkirakan bergantung pada nilai konstanta α> 1/3 .

Statistik untuk memecahkan masalah ke-6. Orang Cina menunjukkan diri mereka dengan sangat baik. Pemain Prancis Vladimir Ivanov juga mendapatkan hasil yang bagus.