Apa musik dalam istilah matematika? Apa itu "la" atau "mi"? Bagaimana tepatnya suara terbentuk dipahami dengan baik pada gitar.
Bunyikan "mi" (suara bebas dari senar pertama), bunyi "la" ( senar pertama dijepit di fret kelima ). "La" adalah 440 Hz. Apa 440 Hz artinya? Itu 440 kali senar bergetar per detik. Bunyi "mi" adalah 5 seminada lebih rendah dari bunyi "la" ( dijepit di fret ke-5 ).

7 seminada lebih rendah, saya akan mendapatkan "mi" lagi, yaitu oktaf. Mengapa bunyi senar pertama dan bunyi senar dijepit pada fret ke-12 disebut dengan kata yang sama "mi"?

Tampaknya bagi kami nada yang sama sedang dimainkan. Faktanya adalah bahwa panjang senar pada titik ini ( "mi" pada fret ke-12 ) dibagi menjadi dua:
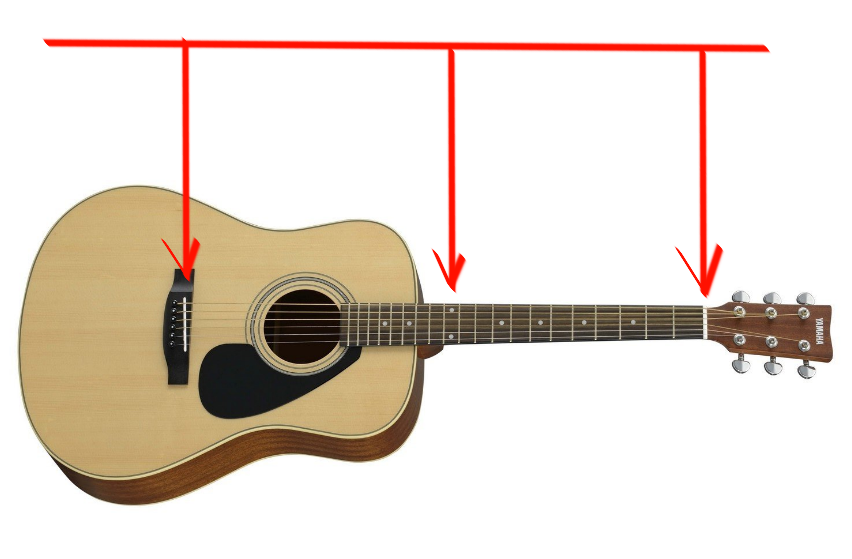
Ini berarti bahwa getaran dari sisa senar ini, menurut hukum fisika, akan dua kali lebih sering dari getaran senar penuh.
Setiap kali saya mundur ke bawah senar dan menjepitnya di fret berikutnya ( pembagian yang ditunjukkan oleh garis tegak lurus di papan fret ), suara naik satu setengah nada, seperti yang dikatakan para musisi.
Perhatikan bahwa fret pada fretboard memiliki lebar yang berbeda. Mereka secara bertahap meruncing, karena untuk menaikkan frekuensi satu semitone, Anda perlu mengurangi panjang string beberapa kali.
Apa yang saya maksud dengan berfokus pada fakta bahwa sesuatu yang "pada" diterjemahkan menjadi sesuatu "dalam"? Matematikawan akan mengatakan bahwa hanya ada satu fungsi (dalam kondisi tertentu) di mana + menjadi x ( perkalian ). Dan fungsi ini disebut logaritma.
Ini berarti telinga kita, memperpendek senar dan menaikkan suara beberapa kali, dianggap menaikkan satu setengah nada. Artinya, setiap fret memperpendek senar dengan jumlah yang sama, dan telinga kita mengatakan bahwa kita naik satu semitone, mencapai nada "E" dan mendapatkan satu oktaf. Organ pendengaran kita logaritmik.
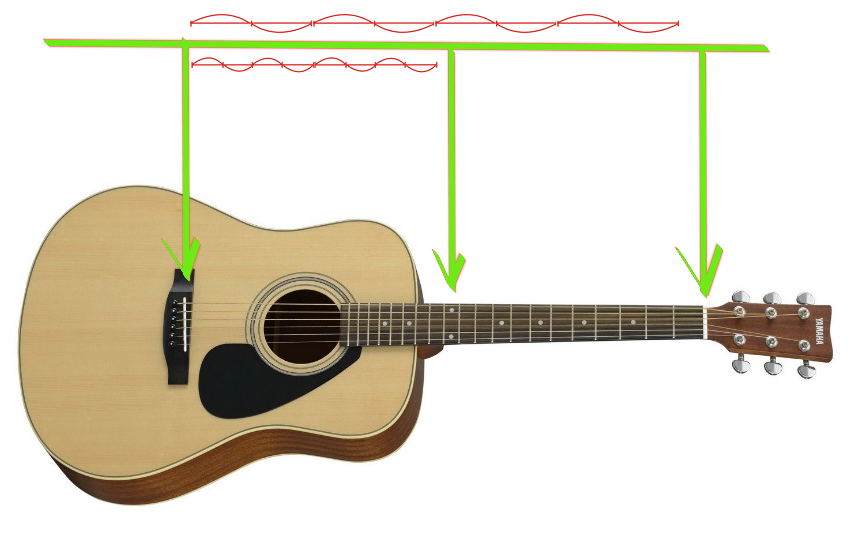
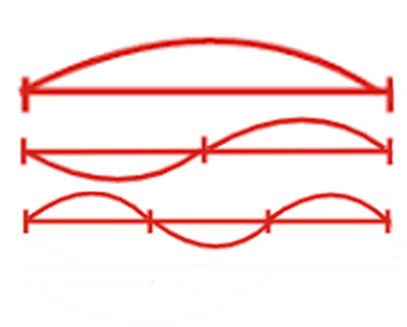
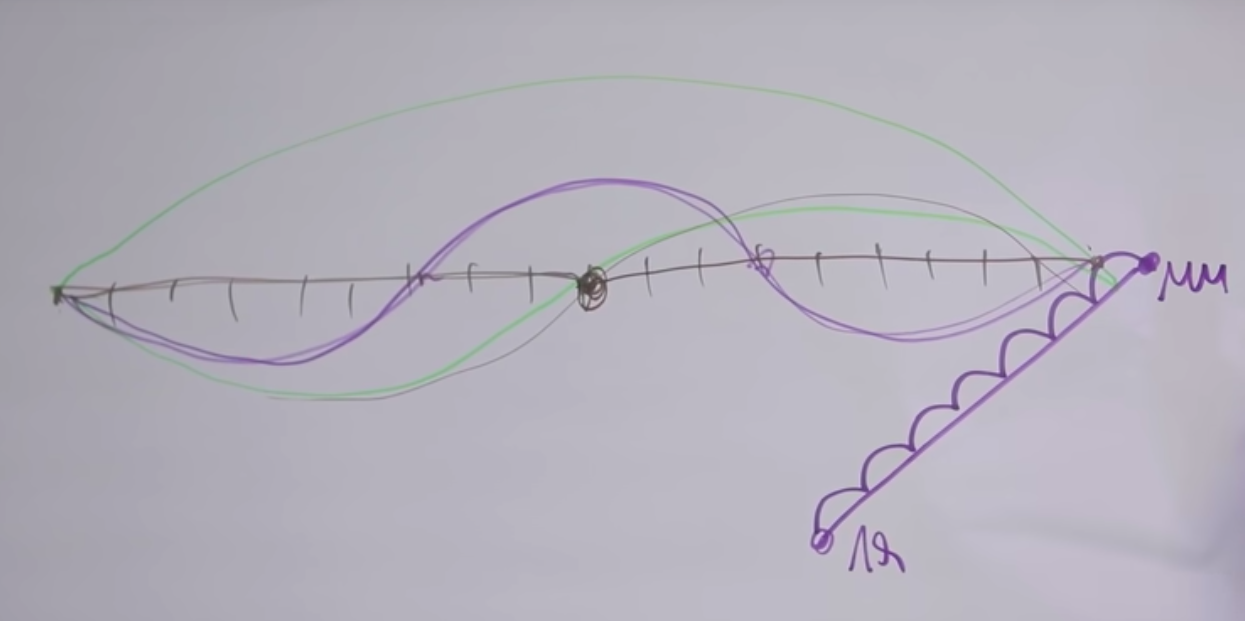
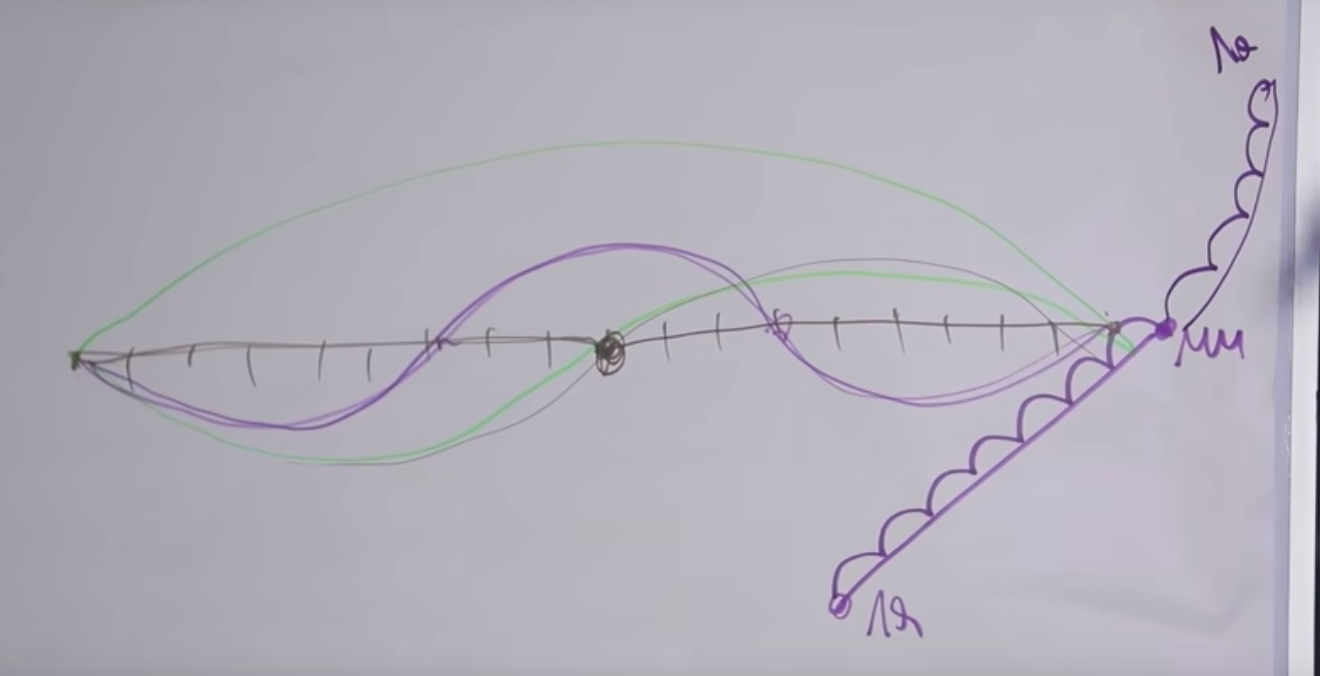
Kami mengatakan bahwa "mi" dan "mi" adalah dua kali berbeda, ini terbukti dari suaranya. Busur atas adalah ayunan penuh. Saat kita menjepitnya di tengah, senar itu mulai bergetar, seperti pada grafik di tengah.
Mengapa suaranya mirip? Faktanya adalah bahwa seiring dengan getaran utama senar, ternyata getaran dari senar yang sama terjadi pada semua frekuensi, dimana panjang bagian getaran berbanding terbalik dengan frekuensi.
Karenanya, jika panjangnya berkurang beberapa kali bilangan bulat, maka nada tambahan yang sesuai dapat didengar. Overtone yang sesuai direalisasikan oleh string yang diberikan. Jika senar tertentu bergetar sebagian tetap pada dua titik ini ( grafik bawah ), maka nadanya akan tiga kali lebih tinggi.
Peningkatan frekuensi dua kali lipat dianggap oleh telinga sebagai nada yang sama. Semua nada tambahan itu kami bagi beberapa kali, mis. pembagian apa pun dari setengah segmen merupakan pembagian otomatis dan segmen besar. Dan hanya beberapa divisi dari segmen besar yang tidak cocok dengan skema setengah divisi.
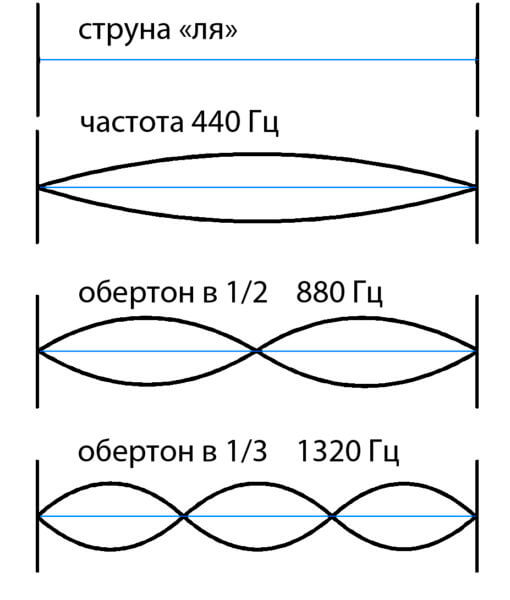
Jika kita mengambil nada atas genap untuk string panjang, maka itu akan menjadi nada atas untuk string yang setengah dipendekkan. Dan benar-benar suara pendek apa pun dari string pendek akan berbunyi untuk yang panjang. Oleh karena itu, kami merasa bahwa semua yang kami dengar bertepatan pada titik-titik ini, dan kami melihatnya sebagai satu nada.
Bahkan lebih menarik bahwa ada nada yang melewati beberapa semitone, dan mereka dianggap oleh telinga kita sebagai konsonan, akord, sesuatu yang enak didengar, tidak memotong telinga kita. Apa catatan ini?
Jika Anda mengambil 7 seminada, catat "A" dan naikkan suara sebanyak 7 seminada, hingga "E" berikutnya, maka kedua nada tersebut akan terdengar bagus.
Jika Anda mundur 5 seminada lagi, maka akan ada "la" yang lebih tinggi pada oktaf berikutnya. Untuk beberapa alasan, interval ini juga terdengar menyenangkan bagi kami. Mari kita cari tahu semuanya.
Pertama-tama, jika peningkatan sebesar 1 semitone adalah peningkatan frekuensi osilasi beberapa kali, maka kita akan menetapkannya sebagai x. Jika Anda perlu menaikkan satu seminada lagi, maka sudah ada x * x, yaitu x 2 . Jika saya menaikkannya 12 seminada (x 12 ), maka itu harus dinaikkan tepat 2 kali. Kami mendapatkan persamaan x 12 = 2.
Oleh karena itu, peningkatan 1 semitone berarti kontraksi string pada x = 12√2, atau, yang sama, menaikkan frekuensi suara sebesar 12 √2.
Dan apa hubungannya "la" dan "mi" dengan itu? Mengapa 7 seminada terdengar melodi? Mari naikkan derajatnya:
Apa yang menyenangkan, bagus dalam angka ini?
Kadang-kadang di zaman kuno, klavikula temper, rekaman musik yang akurat, ditemukan. Anda dapat melihatnya dengan sangat baik di gitar, Anda juga dapat menemukannya di piano, tersembunyi di dalam, jika Anda melihat ke dalam, Anda dapat melihat senarnya.
Sekarang, angka ini hampir mendekati 3/2. Jika Anda menghitung dengan kalkulator, hasilnya akan sangat akurat. Ini berarti bahwa "mi" kira-kira 1,5 kali lebih tinggi dari "la" sebelumnya. Itu. mengangkat 7 nada setara dengan naik 3/2 kali, yang berarti kita memiliki banyak nada atas secara bersamaan.
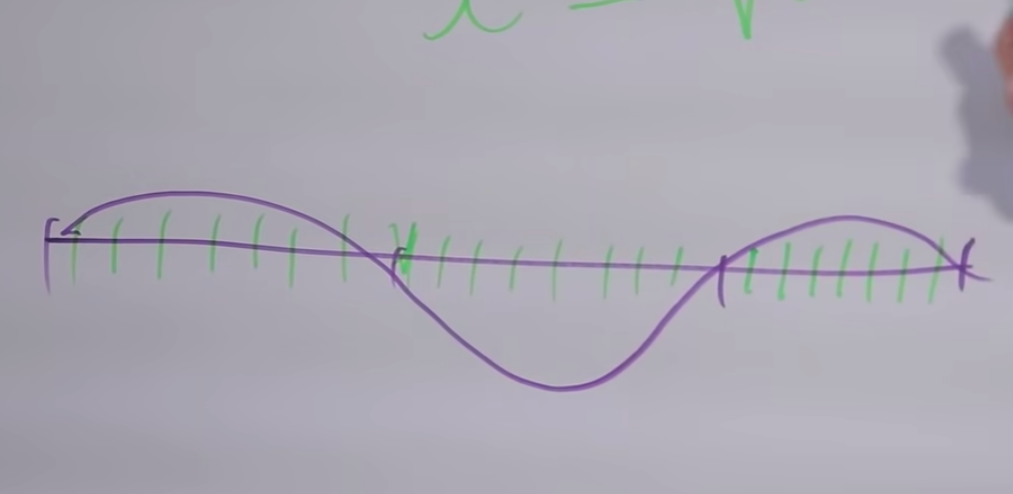
Karena setiap pembagian dengan integer dari segmen kecil akan menjadi divisi integer dari keseluruhan segmen. Dan, dengan demikian, membagi potongan asli dengan jumlah potongan, kelipatan tiga, akan menjadi pembagian segmen kecil (⅓), dan ⅔ juga. Ketika kami meninggalkan ⅔ dari panjangnya, mis. menaikkan frekuensi menjadi 3/2, kami naik sekitar 7 seminada, kami akan memiliki banyak nada tambahan yang sama, itu akan menjadi kesesuaian yang menyenangkan.
Sisa 4/3 sama persis dengan 5 seminada yang tersisa, 3/2 x 4/3 = 2, hanya satu oktaf. Yang sesuai dengan rumus x71243. Nilainya sangat mendekati 4/3, tetapi tidak 100%. Bilangan ini tidak rasional, tidak dapat ditulis sebagai pecahan, tidak dapat ditulis sebagai bilangan bulat dibagi dengan bilangan bulat.
Saya dengar ada alat musik di India ( sitar), di mana oktaf dibagi menjadi 19 bagian, yaitu mereka memiliki semitone = 1/19 oktaf, 19x2.

Dan sudah dengan akurasi tinggi x121932, yang berarti jika pada instrumen India seperti itu Anda mundur 12 dari 19 segmen, maka dalam kesesuaian ini akan ada lebih banyak nada yang bertepatan, dan interval ini terdengar seperti balsem untuk telinga.
Ada banyak hal menarik untuk dikatakan tentang musik dan matematika. Secara khusus, akord mayor dirasakan jika 4 seminada ditambahkan ke nada awal apa pun, dan kemudian 3, yaitu 0 - 4 - 3. A minor, jika Anda menambahkan 3 di awal, lalu 4, yaitu 0 - 3 - 4. Nada pertama dan terakhir dari tiga nada akor akan "sama", hanya berbeda 7 seminada, tetapi bunyi tengah akan menciptakan persepsi kita tentang kesesuaian, dan menyetel dalam mode minor atau mayor.
Tampaknya musik dan matematika, apa kesamaannya? Dan ada begitu banyak kesamaan sehingga matematikawan dan musisi sering berkomunikasi, terlebih lagi, matematikawan dengan mudah memahami musisi, jadi untuk berbicara, mereka memahami semitone.
Beberapa tautan berguna:
- Teori musik untuk para geek
- Notasi tidak diajarkan dengan benar *
- Mengapa ada begitu banyak matematika dalam musik?