Halo kolega! Saya sudah seratus tahun tidak menulis tentang Habr, tapi sekarang waktunya telah tiba. Musim semi ini, saya mengajar kursus ML Lanjutan di MADE Big Data Academy dari Mail.ru Group; Tampaknya para pendengar menyukainya, dan sekarang saya diminta untuk tidak terlalu banyak menulis posting iklan melainkan posting pendidikan tentang salah satu topik kursus saya. Pilihannya hampir pasti: sebagai contoh model probabilistik yang kompleks, kami membahas model SIR epidemiologis yang sangat relevan (tampaknya ... tetapi lebih lanjut nanti) yang memodelkan penyebaran penyakit dalam suatu populasi. Ia memiliki segalanya: perkiraan inferensi melalui metode Markov Monte Carlo, dan model Markov tersembunyi dengan algoritme stokastik Viterbi, dan bahkan data khusus kehadiran.



Dengan topik ini, hanya satu kesulitan kecil yang muncul: Saya mulai menulis tentang apa yang sebenarnya saya ceritakan dan tunjukkan di ceramah ... dan entah bagaimana dengan cepat dan tak terlihat dua puluh halaman teks (yah, dengan gambar dan kode) terkumpul, yang masih belum terkumpul. selesai dan tidak mandiri sama sekali. Dan jika Anda menceritakan semuanya sedemikian rupa sehingga jelas dari "nol" (bukan dari nol mutlak, tentu saja), maka Anda dapat menulis seratus halaman. Jadi suatu hari nanti saya pasti akan menulisnya, tetapi untuk saat ini saya sampaikan kepada Anda bagian pertama dari deskripsi model SIR, di mana kita hanya dapat mengajukan masalah dan mendeskripsikan model dari sisi penghasilnya - dan jika publik yang dihormati memiliki minat, maka itu akan mungkin memproses.

Model SIR: pernyataan masalah

Saya mencintai teman-teman saya dan mereka mencintai saya,

Kami sedekat mungkin.

Dan hanya karena kami benar-benar peduli,

Apa pun yang kami dapat, kami berbagi!



Tom Lehrer. Saya Mendapatnya Dari Agnes

Jadi mari kita cari tahu. Secara informal, asumsi dasar model SIR adalah sebagai berikut:

• ada populasi orang tertentu di mana beberapa virus yang mengerikan dapat berjalan;
• awalnya, virus memasuki populasi dengan satu atau lain cara (misalnya, orang pertama yang sakit muncul), dan kemudian orang-orang menjadi terinfeksi satu sama lain;
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

Sederhananya, kami akan berasumsi bahwa mereka yang pernah sakit selalu mengembangkan kekebalannya, dan mereka dikeluarkan dari siklus virus di alam. Karenanya, transisi antara status ini hanya dapat dilakukan dari kiri ke kanan: Rentan → Terinfeksi → Dipulihkan.



Sebenarnya, tugasnya adalah melatih model ini, yaitu memahami sesuatu tentang parameter proses infeksi dari data. Sangat mudah untuk memahami bagaimana datanya terlihat - ini hanyalah jumlah terdaftar terinfeksi setiap saat, yang akan kami tunjukkan dengan vektor$$$\boldsymbol{y}$... Misalnya, ketika saya memberikan pekerjaan rumah saya dalam kursus tentang virus corona (namun, tentang model lain), data untuk Rusia terlihat seperti ini:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

Tetapi apa parameter dari model ini, bagaimana mereka berinteraksi satu sama lain dan bagaimana melatihnya, terutama pada kumpulan data yang sangat kecil, adalah pertanyaan yang lebih serius.



Secara umum, saya akan mengikuti garis besar pekerjaan ( Fintzi et al., 2016 ), yang membangun algoritma MCMC untuk model SIR, SEIR dan beberapa variannya. Namun dibandingkan dengan ( Fintzi et al., 2016 ), saya akan sangat menyederhanakan model dan penyajiannya. Penyederhanaan utama adalah bahwa alih-alih waktu kontinu, yang dianggap dalam karya asli, kami akan mempertimbangkan waktu diskrit, yaitu, alih-alih proses berkelanjutan yang pada titik tertentu menghasilkan peristiwa jenis "terinfeksi" dan "pulih", kami akan mempertimbangkan bahwa orang melewati serangkaian titik waktu yang berbeda$$$t=1,\ldots,T$... Penyederhanaan ini akan memungkinkan kita, pertama, untuk menghilangkan banyak kesulitan teknis, dan kedua, untuk beralih dari algoritma Metropolis-Hastings secara umum ke algoritma pengambilan sampel Gibbs, yaitu, tidak menghitung rasio Metropolis, seperti yang perlu dilakukan di ( Fintzi et. al., 2016 ). Jika Anda tidak mengerti apa yang baru saja saya katakan, jangan khawatir: kami tidak membutuhkannya hari ini, dan jika ada bagian selanjutnya, saya akan menjelaskan semuanya di sana.



Kami akan menunjukkan status model SIR masing-masing dengan S, I, dan R, dan status seseorang$$$i$ saat ini $$$t$ - di seberang $$$x_i^{(t)}\in\{S, I, R\}$... Pada saat yang sama, kami akan segera memperkenalkan variabel untuk jumlah total pasien yang belum sakit.$$$S^{(t)}$sakit $$$I^{(t)}$ dan pulih $$$R^{(t)}$ saat ini $$$t$... Total man yang akan kita miliki$$$N$jadi untuk siapapun $$$t$ akan dieksekusi $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... Dan, seperti yang saya tulis di atas,$$$y^{(t)}$dari mereka terdaftar (diuji) orang sakit.



Parameter yang tidak diketahui dari model tersebut adalah$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$dimana:

• $$$\boldsymbol\pi$ - distribusi awal kasus; dengan kata lain,$$$x^{(1)}_j\sim \boldsymbol{\pi}$ untuk setiap $$$j$; dalam model sederhana kami, kami tidak akan berlatih$$$\boldsymbol\pi$, tetapi kami hanya akan merekam 1-2 kasus pada saat pertama;
• $$$\rho$ - probabilitas menemukan orang yang terinfeksi dalam populasi umum, yaitu probabilitas seseorang $$$x_j$ pada saat ini $$$t$kapan $$$x_j^{(t)}=I$, akan dideteksi dengan menguji dan terdaftar dalam data $$$y^{(t)}$; dengan kata lain, untuk setiap orang yang sakit, kami melempar koin untuk menentukan apakah pengujian akan menemukannya atau tidak, jadi item saat ini adalah$$$y_t$ memiliki distribusi binomial dengan parameter $$$I^{(t)}$ dan $$$\rho$:

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - probabilitas bagi orang yang sakit untuk pulih dalam satu langkah waktu, yaitu probabilitas transisi dari suatu keadaan $$$I$ di negara bagian $$$R$;

DAN $$$\beta$ - Ini adalah parameter paling menarik yang menunjukkan kemungkinan penularan dalam satu hitungan waktu dari satu orang yang terinfeksi . Ini berarti bahwa dalam model kami mengasumsikan bahwa semua orang dalam populasi "berkomunikasi" satu sama lain ("komunikasi" di sini berarti kontak yang cukup untuk penularan penyakit; virus corona ditularkan terutama melalui tetesan udara, tetapi, tentu saja, dimungkinkan untuk memodelkan dan penyebaran penyakit lain; lihat, misalnya, prasasti), dan kemungkinan terinfeksi tergantung pada berapa banyak yang sekarang terinfeksi, yaitu, pada apa yang$$$I^{(t)}$... Kami akan mengasumsikan model paling sederhana, di mana kemungkinan penularan dari satu orang yang terinfeksi adalah$$$\beta$, dan semua peristiwa ini independen, yang berarti probabilitas untuk tetap sehat adalah

$$

$$(1-\beta)^{I^{(t)}}.$$

Asumsi tersebut sebenarnya harus banyak dibahas. Hal yang paling mengejutkan di sini, menurut pendapat pribadi saya, adalah distribusi binomial untuk$$$y^{(t)}$... Melempar koin dengan kemungkinan mendeteksi orang yang terinfeksi adalah hal yang normal, tetapi tidak terlalu realistis bahwa kita melempar koin ini lagi di setiap langkah, yaitu, kita dapat "melupakan" orang yang sudah terdeteksi terinfeksi. Akibatnya, model SIR dapat (dan sering kali) menghasilkan urutan yang sepenuhnya non-monoton$$$\boldsymbol{y}$; ini aneh, tetapi tampaknya tidak berdampak besar pada hasil, dan akan jauh lebih sulit untuk memodelkan proses ini secara lebih realistis.



Selain itu, jelas bahwa model ini ditujukan untuk populasi tertutup, di mana setiap orang "berkomunikasi" dengan semua orang, jadi tidak masuk akal untuk meluncurkannya, katakanlah, untuk Rusia dengan parameter N seratus juta atau untuk Moskow dengan parameter sepuluh juta (dan secara komputasi tidak akan berhasil). Area penting dari ekstensi dan perluasan model SIR dikhususkan untuk ini: bagaimana menambahkan grafik interaksi yang lebih realistis dan kemungkinan infeksi; kita mungkin akan membicarakan hal ini di posting terakhir, terakhir.



Tetapi dengan semua penyederhanaan ini, sekarang, dengan menggunakan parameter di atas, kita dapat menulis matriks probabilitas transisi antar status. Probabilitas ini (lebih tepatnya, probabilitas tertular) bergantung pada statistik umum populasi. Mari kita tentukan vektor status semua orang kecuali$$$x_j$, di seberang $$$\boldsymbol{x}_{-j}$, dan memperluas notasi yang sama ke semua variabel lainnya; misalnya,$$$I_{-j}^{(t)}$ Merupakan jumlah yang terinfeksi pada suatu waktu $$$t$, apalagi $$$x_j$... Kemudian, untuk kemungkinan transisi dari$$$x_j^{(t-1)}$ di $$$x_j^{(t)}$ kita mendapatkan

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

dan dalam semua kasus lainnya

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

Hal yang sama dapat ditulis lebih jelas dalam bentuk matriks probabilitas transisi (urutan baris dan kolom adalah natural, SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

Bagi pembaca yang akrab dengan rantai Markov dan model Markov, tampaknya ini hanya model Markov tersembunyi: ada keadaan tersembunyi, ada distribusi yang jelas dari pengamatan untuk setiap keadaan tersembunyi, transisinya benar-benar Markov, yaitu, keadaan tersembunyi berikutnya hanya bergantung pada yang sebelumnya ... Tapi ada , seperti yang mereka katakan, ada satu peringatan: probabilitas transisi tidak dapat dianggap konstan, mereka berubah seiring perubahan$$$I^{(t)}$dan ini adalah aspek yang sangat penting dari model yang tidak dapat dibuang.



Oleh karena itu, kesimpulan dalam model ini tiba-tiba menjadi jauh lebih sulit daripada model Markov tersembunyi yang biasa (meskipun tidak selalu ada hadiah seperti itu di sana). Namun, meskipun kesimpulannya lebih rumit, itu masih tergantung pada pikiran manusia - di instalasi berikutnya (jika ada) saya hanya akan memberi tahu Anda tentang ini. Dan untuk hari ini, hampir cukup sudah - sekarang mari kita rileks sedikit dan mencoba bermain dengan model ini untuk saat ini dalam pengertian umum.

Contoh Pembuatan Data

Sebagai ahli dan ahli yang hebat, seorang

introvert masuk ke karantina.

***

"Saya tidak bisa bekerja di rumah,"

lebah itu mencoba menjelaskan kepada cacing.

***

Kaganov meninggal sambil bercanda.

Tentu saja, aku sangat kasihan padanya ...



Leonid Kaganov. Karantina

Jika parameter model diketahui, dan Anda hanya perlu menghasilkan lintasan tentang bagaimana penyebaran penyakit dalam populasi akan berkembang, tidak ada yang rumit dalam SIR. Kode di bawah ini menghasilkan contoh populasi menurut model kita; menyatakan saya dikodekan sebagai$$$S=0$, $$$I=1$, $$$R=2$... Seperti yang saya peringatkan, untuk kesederhanaan saya akan berasumsi bahwa pada saat ini$$$t=0$ hanya ada satu orang yang sakit dalam populasi, dan kemudian berlanjut.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Kode ini tidak hanya memberikan data yang sebenarnya $$$\boldsymbol{y}$tetapi juga statistik yang "benar" $$$S^{(t)}$, $$$I^{(t)}$, $$$R^{(t)}$agar dapat divisualisasikan. Ayo lakukan; untuk parameter$$$N=100$, $$$T=20$, $$$\rho=0.1$, $$$\beta=0.2$, $$$\mu=0.3$Anda bisa mendapatkan sesuatu seperti ini:







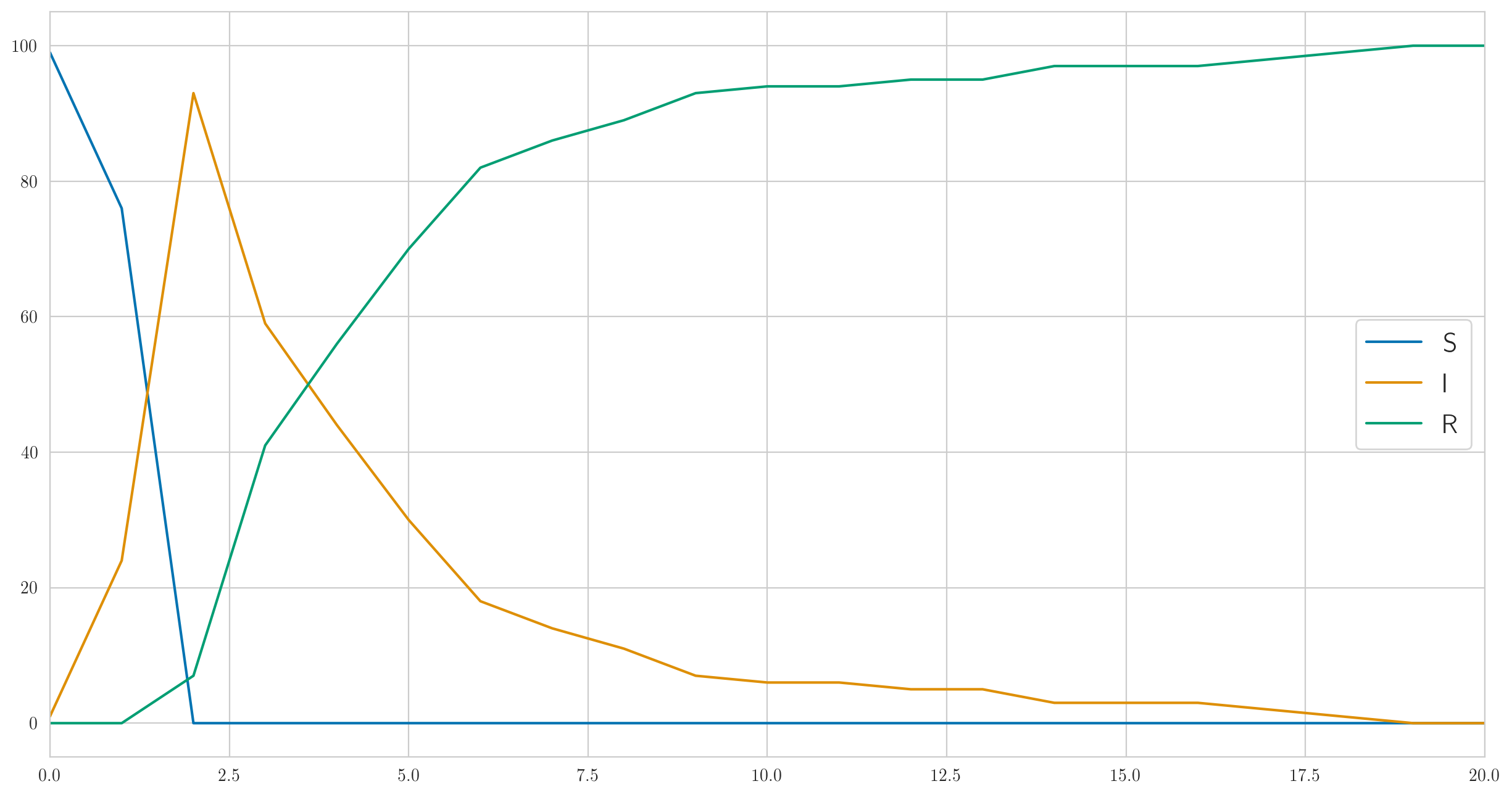
Seperti yang Anda lihat, dalam contoh ini, setiap orang sakit dengan sangat cepat, dan kemudian perlahan mulai membaik. Dan data aktual yang diamati pada orang sakit terlihat seperti ini:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

Perhatikan bahwa, seperti yang kita bahas di atas, tidak ada monoton di sini.



Tapi ini tentunya bukan satu-satunya perilaku yang mungkin. Saya memilih parameter di atas sehingga infeksinya cukup cepat dan penyakitnya hampir segera mencakup semua seratus orang dalam populasi uji kami. Dan jika Anda melakukannya$$$\beta$ lebih kecil, misalnya $$$\beta=0.01$, maka infeksi akan menjadi jauh lebih lambat, dan bahkan tidak semua orang memiliki waktu untuk sakit sebelum orang yang terakhir sakit sembuh dan tidak akan bertahan. Sesuatu seperti ini:







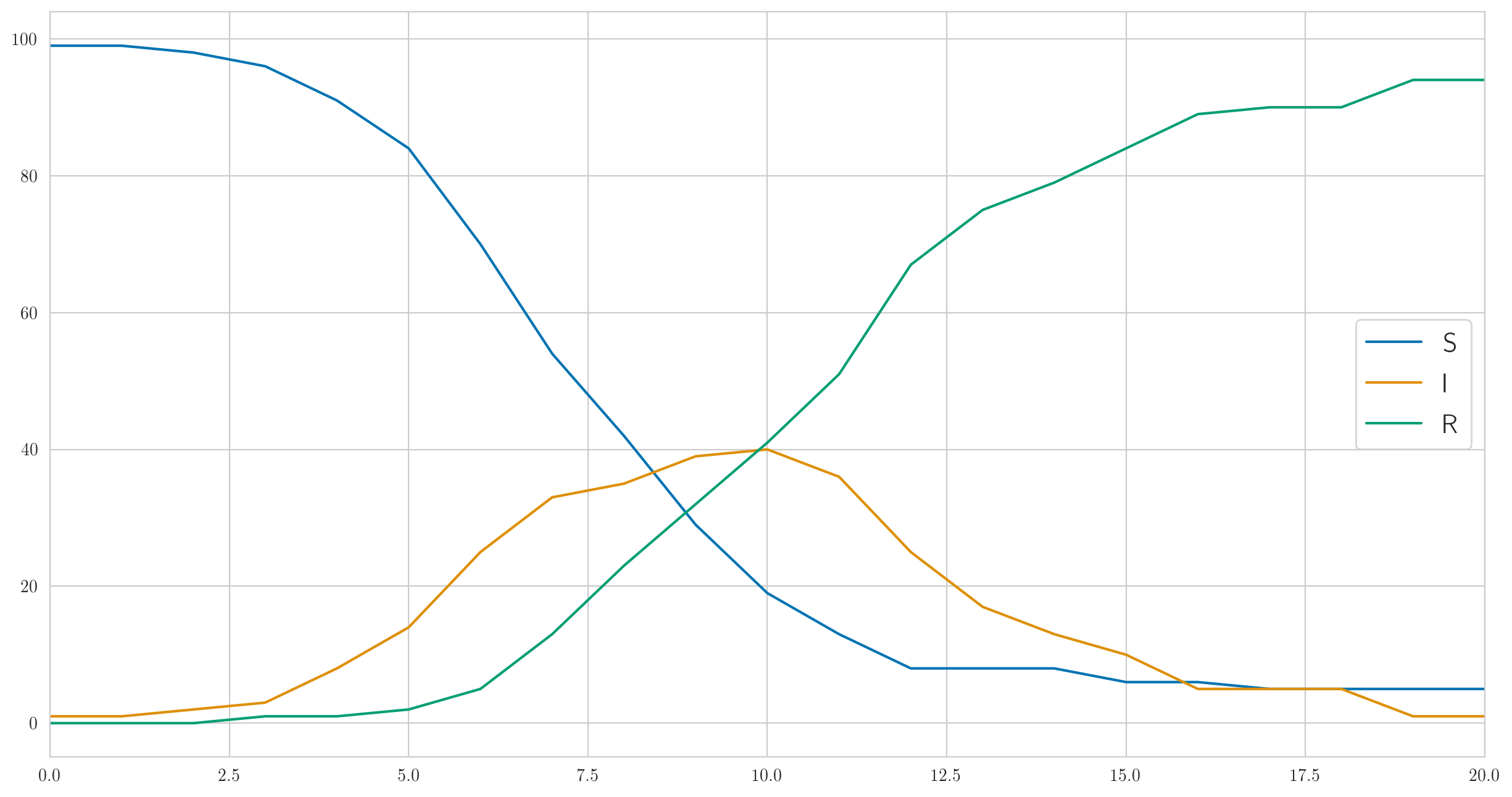
Dan jumlah kasus yang terdeteksi juga sangat berbeda:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

Adalah mungkin untuk lebih "mencekik" penyakit itu; Misalnya, ayo pergi$$$\beta=0.01$tapi taruh $$$\mu=0.5$Artinya, pada setiap interval waktu, setiap orang yang sakit memiliki kesempatan untuk sembuh sebesar 0,5 (pada akhirnya, ini logis: sembuh atau tidak). Kemudian hanya 50-60 dari 100 orang yang akan jatuh sakit karena virus yang mengerikan itu; kurva bisa terlihat seperti ini:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

Tetapi gambaran keseluruhan, tentu saja, dalam beberapa hal terlihat hampir sama: pertumbuhan eksponensial pertama, dan kemudian jalan keluar menuju kejenuhan; satu-satunya perbedaan adalah apakah operator terakhir memiliki waktu untuk pulih sebelum semua orang di-boot ulang.



Nah, inilah waktunya untuk menyimpulkan hasil sementara. Hari ini kita telah melihat seperti apa salah satu model epidemiologi yang paling sederhana. Meskipun banyak asumsi yang terlalu menyederhanakan, model SIR masih sangat berguna bahkan dalam bentuk ini; Faktanya adalah bahwa sebagian besar perluasannya cukup mudah dan tidak mengubah esensi umum masalah. Oleh karena itu, jika kita lanjutkan, pada seri selanjutnya saya akan membahas tentang bagaimana melatih model SIR; Namun, ini akan memerlukan begitu banyak hal menarik yang mungkin juga tidak akan muat dalam satu posting. Sampai Lain waktu!