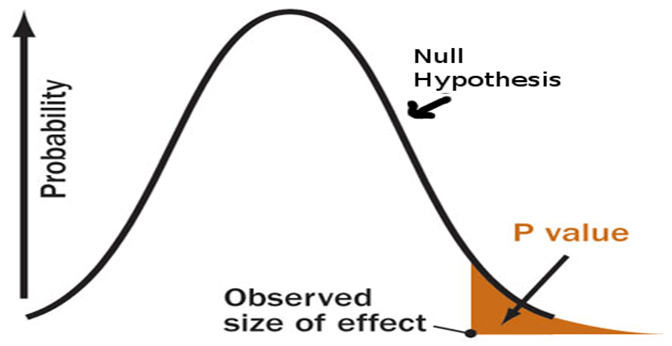
Pada saat itu, saya tidak tahu apa-apa tentang nilai-p, pengujian hipotesis, atau bahkan signifikansi statistik.
Saya memutuskan untuk google kata "p-value" dan apa yang saya temukan di Wikipedia membuat saya semakin bingung ...
Saat menguji hipotesis statistik, nilai p atau nilai probabilitas untuk model statistik tertentu adalah probabilitas bahwa, jika hipotesis nol benar, ringkasan statistik (misalnya, nilai absolut rata-rata sampel dari perbedaan antara dua kelompok pembanding) akan lebih besar dari atau sama dengan hasil observasi aktual.Kerja bagus, Wikipedia.
- Wikipedia
Baik. Saya tidak mengerti apa sebenarnya arti p-value.
Saat saya mendalami lebih dalam bidang ilmu data, saya akhirnya mulai memahami arti dari nilai-p dan di mana ia dapat digunakan sebagai bagian dari alat pengambilan keputusan dalam eksperimen tertentu.
Jadi saya memutuskan untuk menjelaskan nilai-p dalam artikel ini, serta bagaimana hal itu dapat digunakan dalam pengujian hipotesis, untuk memberi Anda pemahaman yang lebih baik dan lebih intuitif tentang nilai-p.
Juga kami tidak dapat melewatkan pemahaman mendasar tentang konsep lain dan definisi nilai-p, saya berjanji bahwa saya akan membuat penjelasan ini intuitif tanpa memaparkan Anda pada semua istilah teknis yang saya temukan.
Ada empat bagian total dalam artikel ini untuk memberi Anda gambaran lengkap dari membangun tes hipotesis hingga memahami nilai-p dan menggunakannya dalam proses pengambilan keputusan Anda. Saya sangat menyarankan Anda untuk mempelajari semuanya untuk mendapatkan pemahaman terperinci tentang nilai-p:
- Pengujian hipotesis
- Distribusi normal
- Apa yang dimaksud dengan nilai-P?
- Signifikansi statistik
Akan menyenangkan.
Ayo mulai!
1. Menguji hipotesis
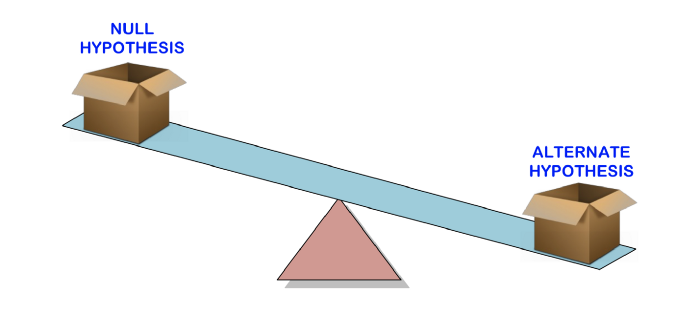
Sebelum kita berbicara tentang apa arti nilai-p, mari kita mulai dengan melihat pengujian hipotesis , di mana nilai-p digunakan untuk menentukan signifikansi statistik dari hasil kita.
Tujuan akhir kami adalah untuk menentukan signifikansi statistik dari hasil kami.
Dan signifikansi statistik dibangun di atas 3 gagasan sederhana ini:
- Pengujian hipotesis
- Distribusi normal
- Nilai-P
Pengujian hipotesis digunakan untuk menguji validitas pernyataan (hipotesis nol) yang dibuat tentang suatu populasi dengan menggunakan data sampel. Hipotesis alternatif adalah salah satu yang akan Anda percayai jika hipotesis nol ternyata salah.
Dengan kata lain, kami akan membuat klaim (hipotesis nol) dan menggunakan data sampel untuk memeriksa apakah klaim tersebut valid. Jika pernyataan tersebut tidak benar, kami akan memilih hipotesis alternatif. Semuanya sangat sederhana.
Untuk mengetahui apakah suatu klaim valid atau tidak, kami akan menggunakan nilai-p untuk menimbang kekuatan bukti untuk melihat apakah itu signifikan secara statistik. Jika bukti mendukung hipotesis alternatif, maka kami menolak hipotesis nol dan menerima hipotesis alternatif. Ini akan dijelaskan di bagian selanjutnya.
Mari gunakan contoh untuk membuat konsep ini lebih jelas, dan contoh ini akan digunakan di seluruh artikel ini untuk konsep lainnya.
Contoh. Misalkan restoran pizza mengklaim memiliki waktu pengiriman rata-rata 30 menit atau kurang, tetapi menurut Anda itu lebih lama dari yang dinyatakan. Jadi, Anda melakukan uji hipotesis dan secara acak memilih waktu pengiriman untuk menguji klaim:
- — 30
- — 30
- , , — — , .
Kami akan menggunakan pengujian satu arah dalam kasus kami, karena yang penting bagi kami adalah waktu pengiriman rata-rata melebihi 30 menit. Kami tidak akan mempertimbangkan kemungkinan ini ke arah lain, karena konsekuensi dari waktu pengiriman rata-rata yang kurang dari atau sama dengan 30 menit bahkan lebih disukai. Di sini kami ingin memeriksa apakah ada kemungkinan waktu pengiriman rata-rata lebih dari 30 menit. Dengan kata lain, kami ingin melihat apakah pizzeria telah menipu kami.
Salah satu cara umum untuk menguji hipotesis adalah menggunakan uji-Z. Kami tidak akan membahas detailnya di sini, karena kami ingin lebih memahami apa yang terjadi di permukaan sebelum menyelam lebih dalam.
2. Distribusi normal
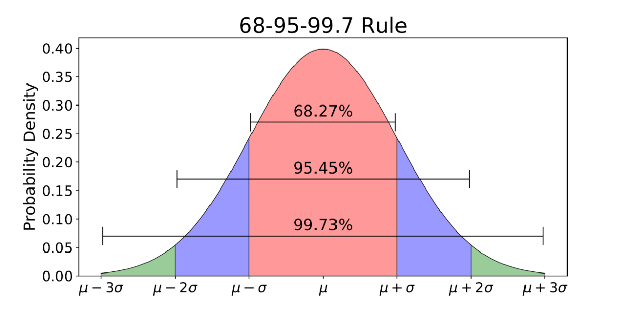
Distribusi normal adalah fungsi kepadatan probabilitas yang digunakan untuk melihat distribusi data.
Distribusi normal memiliki dua parameter, mean (μ) dan deviasi standar, disebut juga sigma (σ).
Rata-rata adalah tren pusat distribusi. Ini menentukan lokasi puncak untuk distribusi normal. Simpangan baku adalah ukuran variabilitas. Ini menentukan seberapa jauh dari rata-rata nilai cenderung turun.
Distribusi normal biasanya dikaitkan dengan aturan 68-95-99,7 (gambar di atas).
- 68% data berada dalam 1 standar deviasi (σ) dari mean (μ)
- 95% data berada dalam 2 standar deviasi (σ) dari mean (μ)
- 99,7% data berada dalam 3 standar deviasi (σ) dari mean (μ)
Ingat ambang lima sigma untuk boson Higgs yang saya bicarakan di awal? 5 sigma adalah sekitar 99.99999426696856% dari data yang harus diterima sebelum ilmuwan mengkonfirmasi penemuan Higgs boson. Ini adalah ambang batas ketat yang ditetapkan untuk menghindari kemungkinan sinyal palsu.
Keren. Sekarang Anda mungkin bertanya-tanya, "Bagaimana hubungan distribusi normal dengan pengujian hipotesis kami sebelumnya?"
Karena kami menggunakan uji-Z untuk menguji hipotesis kami, kami perlu menghitung skor-Z (yang akan digunakan dalam statistik uji kami), yang merupakan jumlah deviasi standar dari rata-rata titik data. Dalam kasus kami, setiap titik data adalah waktu pengiriman pizza yang kami terima. Perhatikan bahwa ketika kami menghitung semua skor-Z untuk setiap waktu pengiriman pizza dan memplot kurva distribusi normal standar seperti yang ditunjukkan di bawah ini, unit pada sumbu X akan berubah dari menit menjadi unit deviasi standar saat kami menstandarisasi variabel dengan mengurangi mean dan membagi itu dengan standar deviasi (lihat rumus di atas). Memeriksa kurva lonceng standar berguna karena kita dapat membandingkan hasil pengujian dengan populasi "normal" dengan satuan standar dalam deviasi standar, terutama bila kita memiliki variabel yang memiliki satuan berbeda.

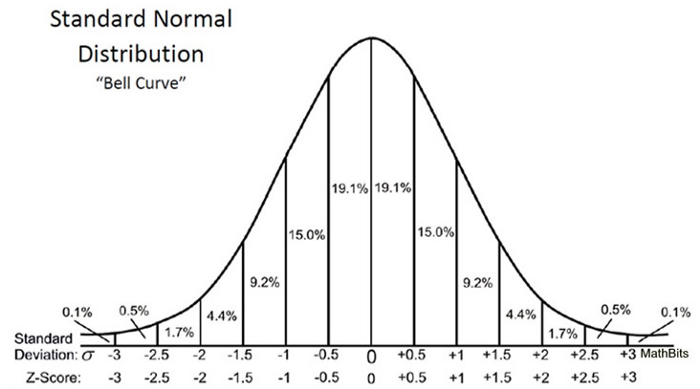
Skor-z dapat memberi tahu kita di mana letak data keseluruhan dibandingkan dengan populasi rata-rata.
Saya suka cara Will Cursen mengatakannya: semakin tinggi atau rendah skor Z, semakin kecil kemungkinan hasil acak dan semakin besar kemungkinan hasil yang berarti.
Tetapi seberapa tinggi (atau rendah) dianggap cukup menarik untuk mengukur seberapa signifikan hasil kami?
Klimaks
Di sini, kami membutuhkan potongan terakhir untuk memecahkan teka-teki, nilai-p, dan memeriksa apakah hasil kami signifikan secara statistik berdasarkan tingkat signifikansi (juga dikenal sebagai alfa) yang kami tetapkan sebelum memulai eksperimen kami.
3. Apa yang dimaksud dengan nilai-P?
Akhirnya ... Kita berbicara tentang nilai-p di sini!
Semua penjelasan sebelumnya dimaksudkan untuk mengatur panggung dan mengarahkan kita ke nilai-P ini. Kita memerlukan konteks dan langkah sebelumnya untuk memahami nilai p yang misterius (sebenarnya tidak begitu misterius) ini dan bagaimana hal itu dapat mengarahkan pada keputusan kita untuk menguji hipotesis.
Jika Anda sudah sampai sejauh ini, teruslah membaca. Karena bagian ini adalah bagian yang paling menarik dari semuanya!
Alih-alih menjelaskan nilai-p menggunakan definisi yang diberikan oleh Wikipedia (maaf Wikipedia), mari kita jelaskan dalam konteks kita - waktu pengiriman pizza!
Sebagai pengingat, kami telah memilih secara acak beberapa waktu pengiriman pizza, dan tujuannya adalah untuk memeriksa apakah waktu pengiriman melebihi 30 menit. Jika bukti akhir mendukung klaim restoran pizza (waktu pengiriman rata-rata adalah 30 menit atau kurang), maka kami tidak akan menolak hipotesis nol. Jika tidak, kami membantah hipotesis nol.
Jadi tugas nilai-p adalah menjawab pertanyaan ini:
Jika saya tinggal di dunia di mana waktu pengiriman pizza adalah 30 menit atau kurang (hipotesis nol benar), seberapa tidak terduga bukti saya dalam kehidupan nyata?Nilai-P menjawab pertanyaan ini dengan angka - probabilitas.
Semakin rendah nilai p, semakin tidak terduga buktinya, semakin konyol hipotesis nol kita.
Dan apa yang kita lakukan ketika kita merasa konyol tentang hipotesis nol kita? Kami menolaknya dan memilih hipotesis alternatif kami.
Jika nilai p di bawah tingkat signifikansi tertentu (orang menyebutnya alfa, saya menyebutnya ambang absurditas - jangan tanya mengapa, lebih mudah bagi saya untuk memahaminya), maka kami menolak hipotesis nol.
Sekarang kita mengerti apa arti p-value. Mari terapkan ini dalam kasus kita.
Nilai-P dalam menghitung waktu pengiriman pizza
Sekarang kami telah mengumpulkan beberapa data sampel tentang waktu pengiriman, kami melakukan perhitungan dan menemukan bahwa waktu pengiriman rata-rata 10 menit lebih lama dengan nilai-p 0,03.
Ini berarti bahwa di dunia di mana waktu pengiriman pizza adalah 30 menit atau kurang (hipotesis nol benar), ada 3% kemungkinan bahwa kita akan melihat waktu pengiriman rata-rata setidaknya 10 menit lebih lama karena kebisingan acak. ...
Semakin kecil nilai p, semakin berarti hasilnya, karena kecil kemungkinannya disebabkan oleh kebisingan.
Dalam kasus kami, kebanyakan orang salah memahami nilai-p:
Nilai-p 0,03 berarti ada 3% (persentase probabilitas) bahwa hasilnya adalah kebetulan - yang tidak benar.Orang sering menginginkan jawaban yang pasti (termasuk saya sendiri), itulah sebabnya saya sudah lama bingung dengan interpretasi nilai-p.
Nilai-p tidak * membuktikan * apa pun. Ini hanya cara untuk menggunakan kejutan sebagai dasar keputusan cerdas.Inilah cara kita menggunakan nilai p 0,03 untuk membantu kita membuat keputusan cerdas (PENTING):
- Cassie Kozyrkov
- Bayangkan kita hidup di dunia di mana waktu pengiriman rata-rata selalu 30 menit atau kurang - karena kita percaya pada restoran pizza (kepercayaan asli kita)!
- Setelah menganalisis waktu pengiriman sampel yang dikumpulkan, nilai-p 0,03 lebih rendah dari tingkat signifikansi 0,05 (dengan asumsi kita menetapkan nilai ini sebelum percobaan kita), dan kita dapat mengatakan bahwa hasilnya signifikan secara statistik.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
Sekarang, Anda mungkin telah menemukan sesuatu ... Bergantung pada konteks kami, nilai-p tidak digunakan untuk membuktikan atau membenarkan apa pun.
Menurut pendapat saya, nilai-p digunakan sebagai alat untuk menantang keyakinan awal kami (hipotesis nol) ketika hasilnya signifikan secara statistik. Saat kita merasa konyol dengan keyakinan kita sendiri (dengan asumsi nilai p menunjukkan bahwa hasilnya signifikan secara statistik), kita membuang keyakinan asli kita (menolak hipotesis nol) dan membuat keputusan cerdas.
4. Signifikansi statistik
Terakhir, ini adalah tahap terakhir di mana kami mengumpulkan semuanya dan memeriksa apakah hasilnya signifikan secara statistik.
Tidak cukup hanya memiliki nilai p, kita perlu menetapkan ambang batas (tingkat signifikansi - alfa). Alfa harus selalu disetel sebelum bereksperimen untuk menghindari bias. Jika nilai p yang diamati lebih rendah dari alpha, maka kita menyimpulkan bahwa hasilnya signifikan secara statistik.
Aturan dasarnya adalah menyetel alpha menjadi 0,05 atau 0,01 (sekali lagi, nilainya bergantung pada tugas Anda).
Seperti yang disebutkan sebelumnya, misalkan kita menetapkan alfa ke 0,05 sebelum memulai percobaan, hasilnya signifikan secara statistik karena nilai p 0,03 lebih rendah dari alfa.
Sebagai referensi, berikut adalah langkah-langkah utama untuk keseluruhan eksperimen:
- Rumuskan hipotesis nol
- Bentuk hipotesis alternatif
- Tentukan nilai alfa yang akan digunakan
- Temukan skor Z yang terkait dengan level alfa Anda
- Temukan statistik uji menggunakan rumus ini
- Jika statistik pengujian kurang dari skor alfa Z (atau nilai p kurang dari nilai alfa), tolak hipotesis nol. Jika tidak, jangan menolak hipotesis nol.
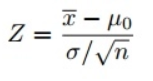
Jika Anda ingin mengetahui lebih banyak tentang signifikansi statistik, silakan membaca artikel ini - Menjelaskan Signifikansi Statistik , yang ditulis oleh Will Kersen .
Refleksi selanjutnya
Ada banyak hal yang perlu dicerna di sini, bukan?
Saya tidak dapat menyangkal bahwa nilai-p secara inheren membingungkan banyak orang, dan saya butuh waktu cukup lama untuk benar-benar memahami dan menghargai nilai-p dan bagaimana mereka dapat diterapkan dalam proses pengambilan keputusan kami. sebagai ilmuwan data.
Tapi jangan terlalu mengandalkan nilai-p, karena mereka hanya membantu sebagian kecil dari keseluruhan proses pengambilan keputusan.
Saya berharap penjelasan saya tentang nilai-p menjadi intuitif dan membantu dalam pemahaman Anda tentang apa arti nilai-p sebenarnya dan bagaimana mereka dapat digunakan dalam menguji hipotesis Anda.
Menghitung nilai p itu sendiri sederhana. Bagian yang sulit datang ketika kita ingin menafsirkan nilai-p dalam pengujian hipotesis. Semoga sekarang bagian yang sulit menjadi sedikit lebih mudah bagi Anda.
Jika Anda ingin mempelajari lebih lanjut tentang statistik, saya sangat menyarankan Anda membaca buku ini (yang saat ini sedang saya baca!) - Statistik Praktis untuk Ilmuwan Data, khusus ditulis untuk ilmuwan data untuk memahami konsep dasar statistik.

Pelajari lebih lanjut tentang cara mendapatkan profesi profil tinggi dari awal atau Naik Level dalam keterampilan dan gaji dengan mengikuti kursus online berbayar SkillFactory:
- Melatih profesi Ilmu Data dari awal (12 bulan)
- Profesi analis dengan level awal apa pun (9 bulan)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )
- Data Sciene 2020
- Data Science . Business Science
- Data Scientist
- Data Scientist -
- 450
- Data Science : «data»
- Data Sciene : Decision Intelligence