Perkiraan linier dari kombinasi garis oleh satu set titik-titik yang berisik

Rumusan masalah

Mari kita pertimbangkan masalah perkiraan kombinasi garis lurus dengan satu set titik koordinat berisik yang terletak pada kombinasi garis tertentu (lihat Gbr. 1 dan Gbr. 2). Rumus biasa dari pendekatan linier tidak akan bekerja di sini, karena titik-titiknya dicampur dan hasilnya adalah beberapa garis rata-rata di antara keduanya (lihat Gambar 3).

Angka: 1 Kombinasi garis dan koordinat berisik

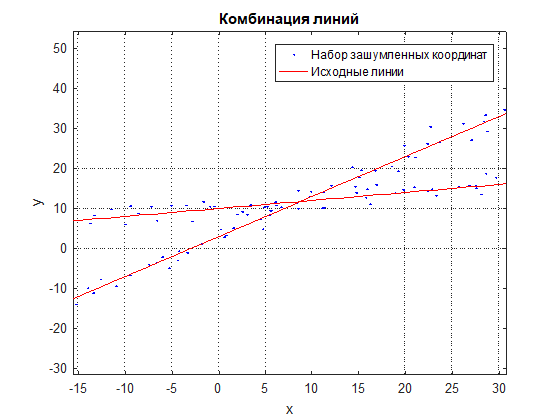
Angka: 2 Kombinasi garis dan kumpulan koordinat yang berisik dalam skala yang diperbesar

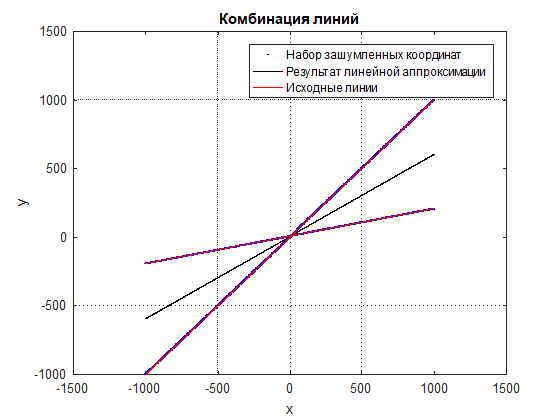
Angka: 3 Hasil pendekatan linier

Algoritma

, , . .. , , -90 +90 ( -180 180 , .. ).

, , . , , . .

, , . , , .

1.

. , . , . -90 90 0.1 .

2.

, .

, , :

y = k x + b, x_{p}, y_{p}

$y = kx + b, x_p, y_p$

, , , :

y - y_{p} = - (x - x_{p}) / k => y = - x / k + x_{p} / k + y_{p}

$y-y_p=-(x-x_p)/k =>y= -x/k+ x_p/k+y_p$

, :

- x / k + x_{p} / k + y_{p} = k x + b => - x + x_{p} + k y_{p} = k^{2} x + b k

$-x/k+ x_p/k+y_p=kx+b => -x+ x_p+ky_p= k^2 x+bk$

- b k + x_{p} + k y_{p} = k^{2} x + x => x = (x_{p} + k y_{p} - b k) / (k^{2} + 1)

$-bk+ x_p+ky_p= k^2 x+x => x= (x_p+ky_p-bk)/(k^2+1)$

y = k (x_{p} + k y_{p} - b k) / (k^{2} + 1) + b = (〖 k x 〗_{p} + k^{2} y_{p} - b k^{2} + b k^{2} + b) / (k^{2} + 1) = (〖 k x 〗_{p} + k^{2} y_{p} + b) / (k^{2} + 1)

$y= k (x_p+ky_p-bk)/(k^2+1)+b= (〖kx〗_p+k^2 y_p-bk^2+bk^2+b)/(k^2+1)=(〖kx〗_p+k^2 y_p+b)/(k^2+1)$

:

d i s t = \sqrt ((x_{p} - (x_{p} + k y_{p} - b k) / (k^{2} + 1))^{2} + (y_{p} - (〖 k x 〗_{p} + k^{2} y_{p} + b) / (k^{2} + 1))^{2})

$dist= √((x_p- (x_p+ky_p-bk)/(k^2+1))^2+(y_p- (〖kx〗_p+k^2 y_p+b)/(k^2+1))^2 )$

3.

, , , (. . 4-6).

. , (. . 7, 8). . 7 , .

. 4 ( )

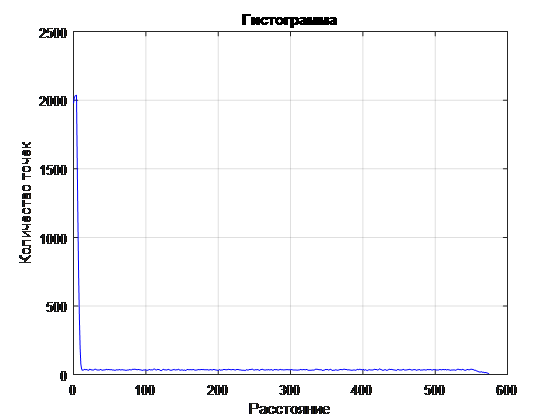
. 5 ( )

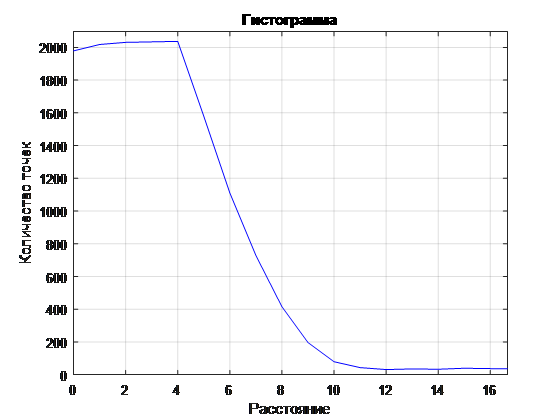
. 6 ( )

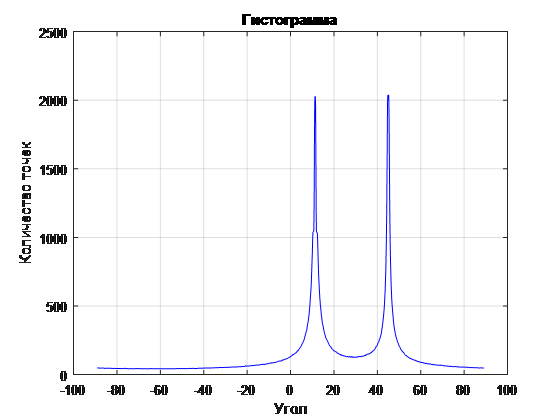
. 7 ( 1)

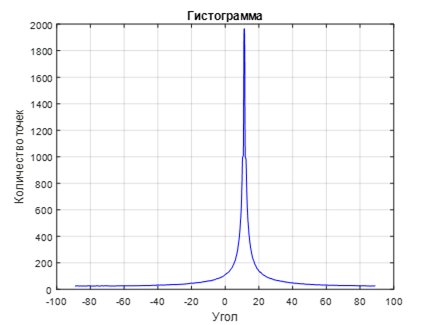
. 8 ( 2)

4.

, . , (. . 9 . 10):

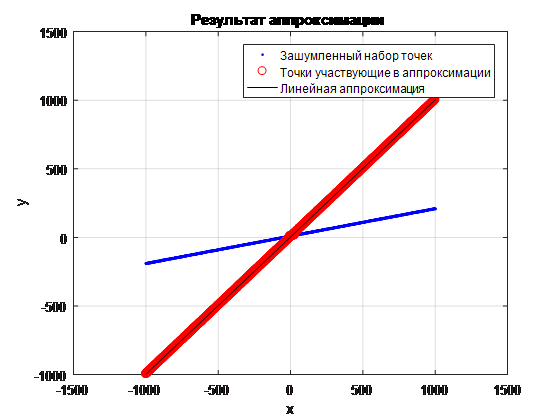
k = (N \sum_{1}^{N} (x y) - \sum_{1}^{N} x \sum_{1}^{N} y) / (N \sum_{1}^{N} x^{2} - (\sum_{1}^{N} x)^{2}); b = (\sum_{1}^{N} y - k \sum_{1}^{N} x) / N

$k= (N∑_1^N(xy)- ∑_1^Nx ∑_1^Ny)/(N∑_1^Nx^2 - (∑_1^Nx)^2 ); b =(∑_1^Ny-k∑_1^Nx)/N$

. 9

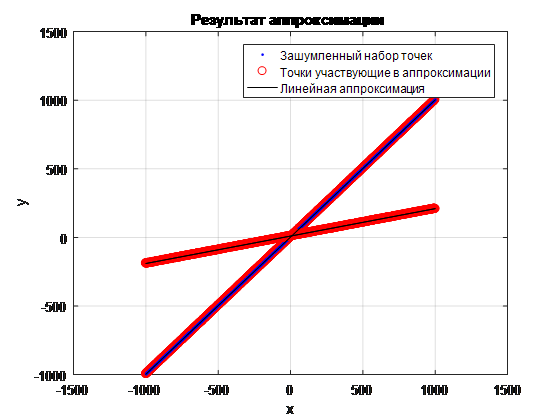
. 10

(. 11-13).

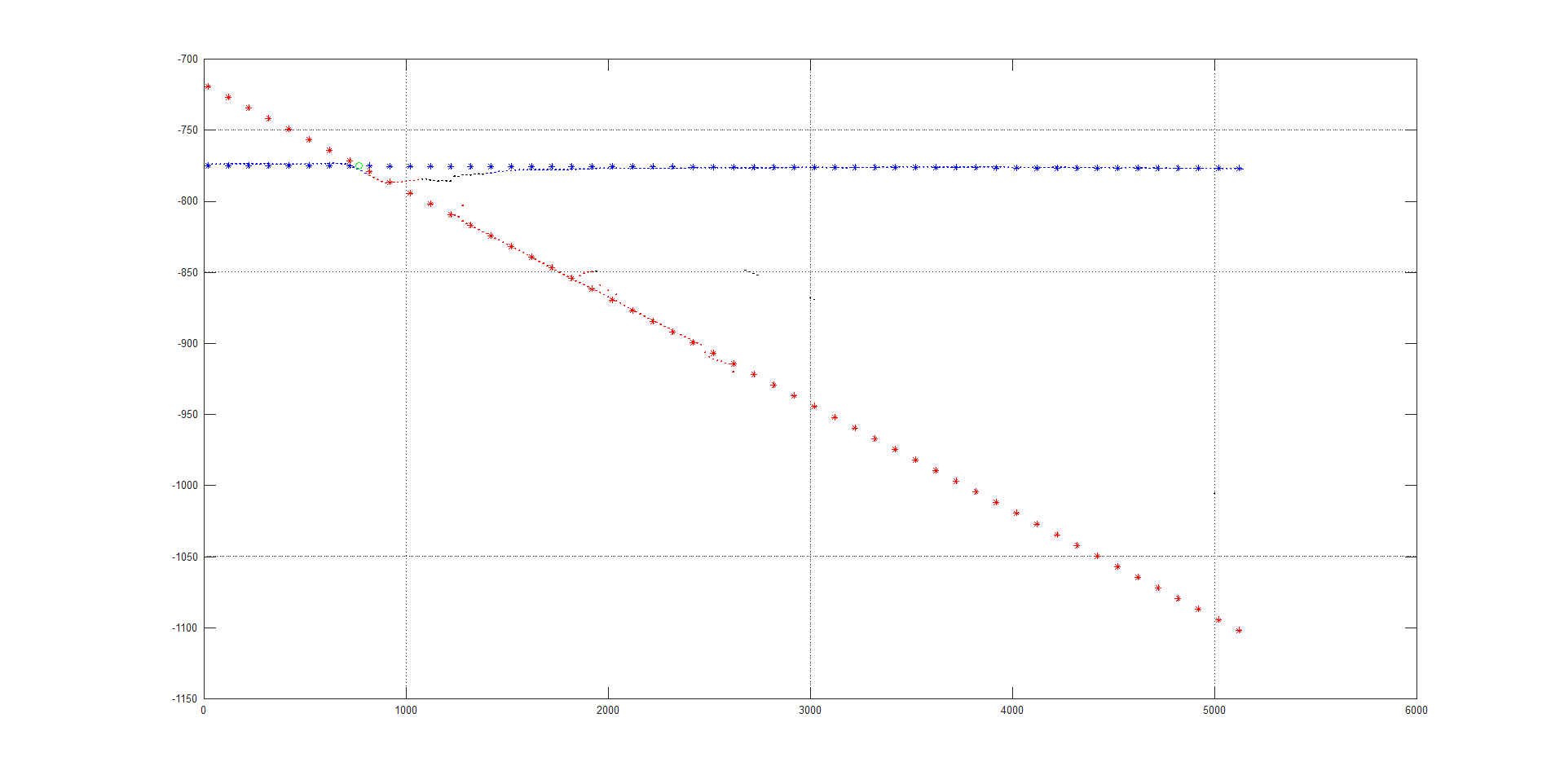
. 11

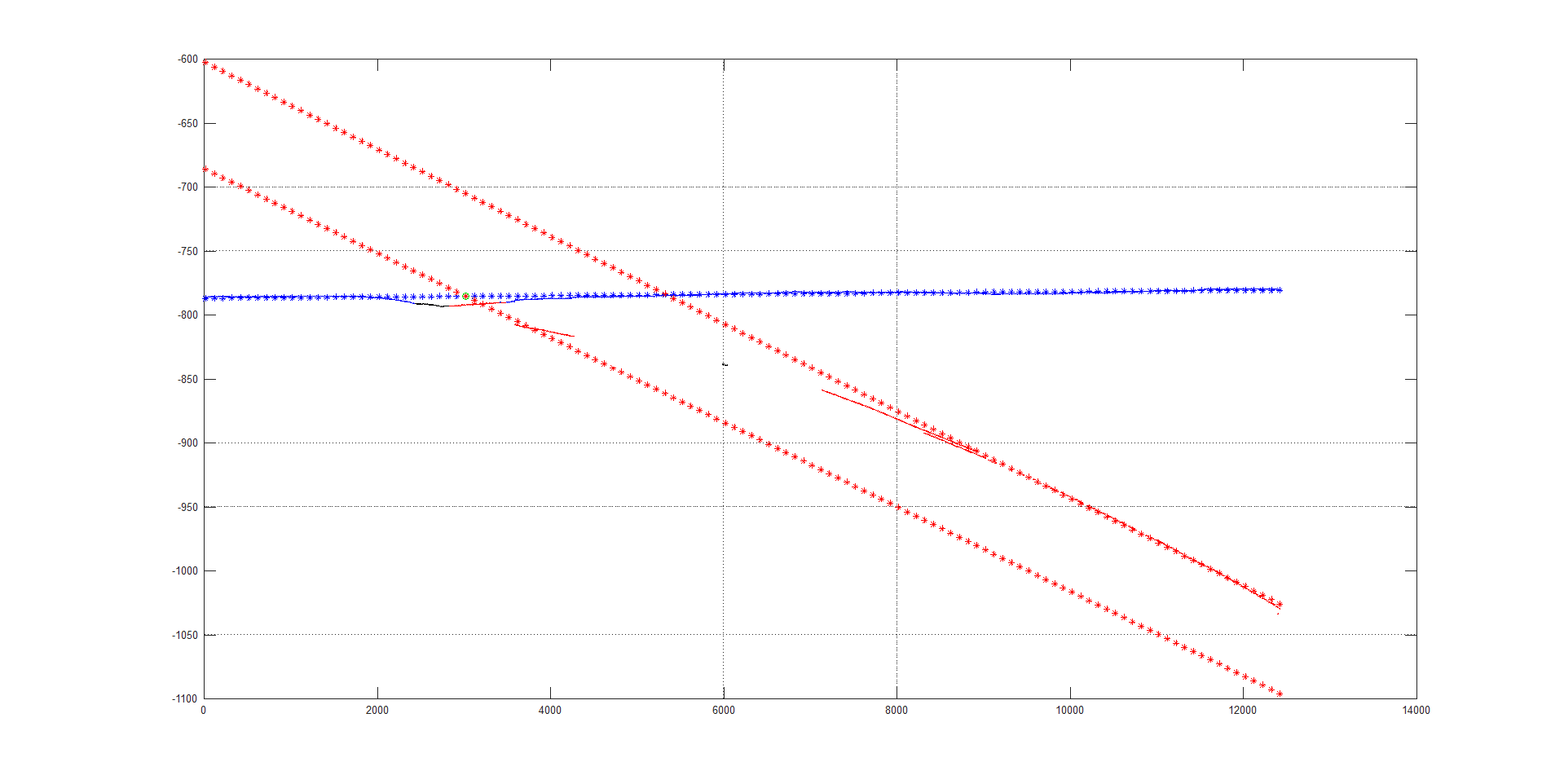
. 12

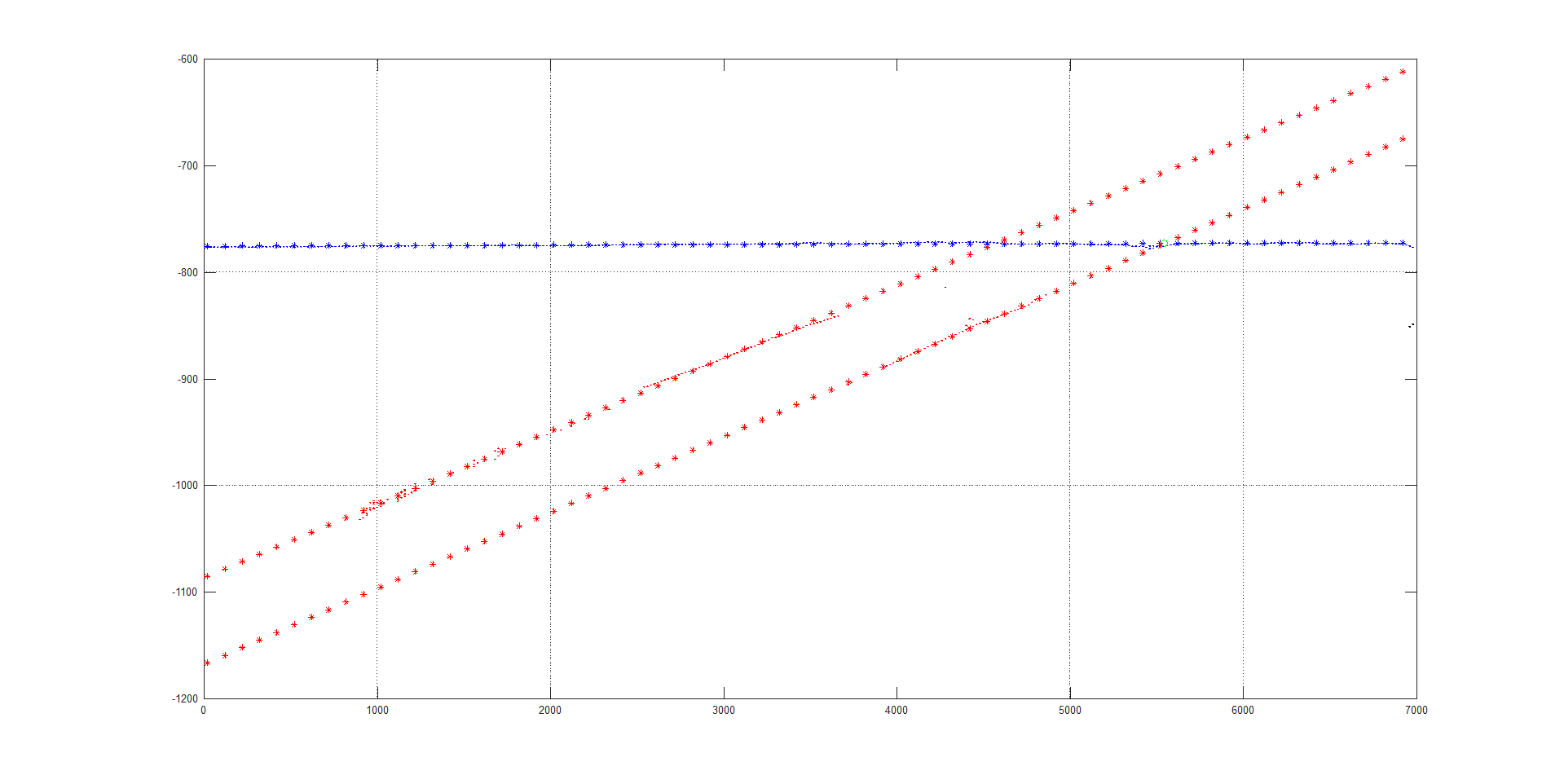
. 13

( ). .

, , , , .

, - . , . - , .

All Articles