AES adalah standar enkripsi Amerika. Bagian V. Serangan

Setelah presentasi terperinci dengan detail transformasi individu, dengan elemen terbatas, bukan abstrak (seperti dalam banyak publikasi, tidak termasuk bidang aljabar Khabrovsky), tetapi ( konkret ), di mana RIJNDAEL, AES-128 dan ( melakukan operasi standar AES-128 ) diimplementasikan , kita dapat melanjutkan untuk mempertimbangkan kemungkinan serangan pada sandi. Untuk saat ini, kami akan membatasi diri pada satu serangan, menurut pendapat kami, yang paling dapat dimengerti dan dibangun secara transparan (meskipun, mungkin, tidak untuk semua pembaca) Habr.



Saya sudah terbiasa dengan kerugiannya, tetapi iblis tidak bercanda. Analisis kemungkinan serangan dan hasil yang diharapkan telah dilakukan oleh banyak penulis, tetapi contoh nyata yang berhasil atau desain yang cukup mengesankan jelas tidak cukup. Di sini kita akan mempertimbangkan dari sudut pandang matematis serangan menggunakan kesalahan yang diperkenalkan oleh penyusup ke dalam ciphertext. Ketika memilih serangan untuk demonstrasi, penulis mencoba untuk tidak melibatkan mereka yang menggunakan hal-hal matematika yang terlalu rumit dan rumit, tetapi subjek yang dimaksud cukup serius dan tidak memungkinkan untuk melanjutkan ke penjelasan dengan "jari".



Tujuan penting dari publikasi ini adalah untuk menunjukkan penerapan matematika, yang menjadi dasar dari AES-128, dan yang sayangnya, banyak penulis mengabaikan atau salah menafsirkan tidak berdasar dan tidak berdasar, dipandu oleh fakta bahwa hanya sedikit yang dapat memeriksa dan menunjukkan penemuan mereka.



Materi artikel tidak sepenuhnya konsep asli serangan, tindakan utama diambil dari pekerjaan , tetapi itu dikerjakan dengan hati-hati, ditambah dan diuji secara eksperimental oleh siswa saya. Mereka mendapat praktik yang baik dalam aljabar dan kriptologi tingkat tinggi.

1. Serangan pada kunci sandi AES

Pertama, serangan terhadap AES dijelaskan dalam kasus sederhana, dan kemudian menjadi jelas bagaimana serangan tersebut dapat digeneralisasikan. Tujuan dari serangan yang sedang dipertimbangkan adalah untuk memulihkan kunci K (Nr) dari sandi tersebut. Setelah kunci parsial (bulat) K (Nr) ditentukan, menjadi mudah untuk mendapatkan kunci K.

1.1 Prinsip serangan

Diasumsikan bahwa dimungkinkan untuk mengubah dengan memasukkan kesalahan "ε" ke dalam byte terpisah dari matriks status S (salah satu dari 16) setelah operasi ShiftRows (Nr - 1), yaitu putaran kedua dari belakang, dan indeks (# sel) dari byte yang rusak (elemen ) negara bagian. Hipotesis terakhir ini dapat dihilangkan; ini diperkenalkan untuk menjelaskan mekanisme serangan dengan lebih mudah. Nilai baru dari item negara diasumsikan tidak diketahui.



Kesalahan "ε" meluas hingga tidak lebih dari empat byte status keluar dari proses. Untuk semua 4 elemen yang dapat diubah dari status keluaran, satu set nilai (himpunan) vektor dari kemungkinan kesalahan "ε" ditemukan di bagian 1.4. Selain itu, menjadi mungkin untuk memotong himpunan nilai yang mungkin "ε" (definisi 1) untuk keempat elemen ini. Ketika himpunan tersebut berpotongan, himpunan yang lebih kecil diperoleh, dan dengan demikian jumlah ciphertext yang diperlukan untuk analisis lengkap berkurang.



Akhirnya, untuk setiap kesalahan, kami mencetak beberapa kemungkinan nilai yang kacau untuk empat elemen dari kunci bulat sebelumnya. Membentuk ciphertext lain, kami menemukan empat byte dari kunci bulat K (10). Serangan ini tetap berhasil bahkan dengan banyak asumsi umum tentang lokasi kesalahan. Seperti kurangnya informasi tentang lokasi kesalahan sebelum transformasi MixColumns () ke-9. Perbedaan antara matriks teks sandi dengan dan tanpa distorsi akan menunjukkan distorsi dan posisinya (dalam contoh adalah posisi 0,7,10,13).



Juga disarankan bahwa kesalahan "ε" yang diperkenalkan pada putaran 8 (sebelum transformasi MixColumns () ke-8) dapat berguna untuk analisis. Tetapi pada saat yang sama, jumlah teks sandi yang diperlukan untuk analisis yang lebih lengkap meningkat. Untuk contoh numerik yang dipertimbangkan, sekitar sepuluh ciphertext diperlukan untuk mendapatkan empat byte kunci bulat K (10), dalam kondisi di mana hipotesis lokasi kesalahan tidak dipertimbangkan.

1.2 Contoh numerik dari dampak kesalahan pada pesan

Di sini contoh yang sama digunakan seperti yang diberikan dalam Lampiran karya bernama . Putaran kedua dari belakang dan terakhir dari proses enkripsi dipertimbangkan (representasi byte dari data memiliki bentuk berikut):



Input = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 ';

Kunci sandi = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';

Keluaran = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 ';

Kesalahan "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00'.



Diagram berikut menunjukkan nilai-nilai yang terdapat dalam array status menurut panjang blok sandi dan panjang kunci sandi masing-masing 16 byte (yaitu, Nb = 4 dan Nk = 4).



Penyebaran kesalahan ditampilkan dalam notasi tebal dan heksadesimal. Di bawah ini adalah kuadrat Negara Bagian dalam situasi yang berbeda:





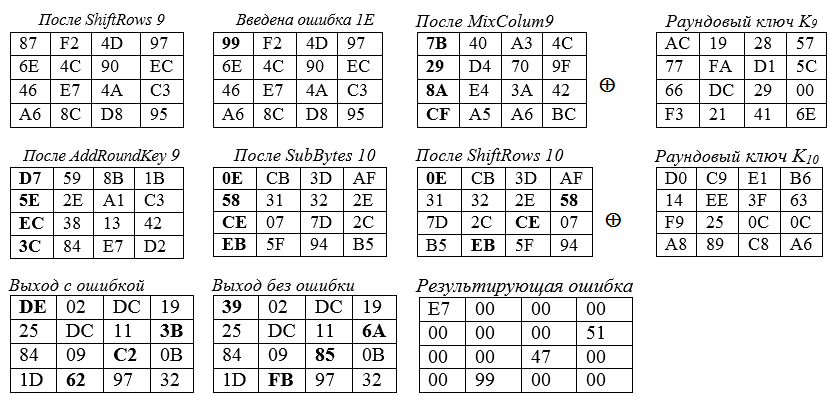
Kesalahan "ε" = 1E, dimasukkan ke dalam byte ke-0 dari status putaran ke-9, menghasilkan perubahan dalam empat byte dari status akhir. Contoh perhitungan untuk sel sudut diagonal utama "persegi" negara bagian:



- kesalahan "ε" = 1E



87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99 dimasukkan ke dalam sel kiri atas (sudut) dari kuadrat Negara putaran ke-9

- kanan bawah Keadaan sudut putaran ke-9 setelah MixColum9 dijumlahkan dengan byte kunci K (9):



BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.

- menghitung nilai kesalahan yang dihasilkan.



Di hadapan dua teks pesan, dengan dan tanpa kesalahan, nilai dan posisi byte status yang rusak ditentukan dengan mengurangkan satu teks dari yang lain. Dalam kasus kami, pengurangan seperti itu dapat diganti dengan menjumlahkan teks modulo dua. Kami mendapatkan hasil bukan nol hanya untuk byte yang diubah oleh kesalahan yang dimasukkan ke dalam teks sumber.



Misalnya, dalam bentuk heksadesimal, kami menemukan nilai kesalahan:



Tabel 7 - perhitungan nilai kesalahan







Akibatnya, kesalahan perbedaan$$$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$... Mari kita berikan contoh penghitungan byte kesalahan terakhir:



62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.



Posisi byte status diubah oleh kesalahan

$$$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$Tunjukkan indeks untuk elemen kunci bulat (putaran terakhir), seperti K [0], K [7], K [10], K [13]. Di sini, 0, 7, 10, 13 adalah nomor sel dari matriks keadaan, dan matriks Ao adalah matriks transformasi untuk mencampur kolom-kolom proses enkripsi, yang kolom pertamanya berbentuk: '02', '01', '01', '03'.

Bagaimana Kesalahan yang Disuntikkan Mempengaruhi Status Akhir Akhir

Analisis informasi yang diperoleh ketika kesalahan diperkenalkan

Satu-satunya operasi yang dapat berisi informasi tentang kunci K (Nr) adalah transformasi SubBytes () terakhir. Oleh karena itu, kami memiliki empat persamaan, di mana x0, x1, x2, x3, ε adalah variabel yang tidak diketahui.



Kami ingin mendapatkan solusi untuk empat persamaan berikut:

$$$s(x_0 +2ε) + s(x_0) =ε_0’,$

$$$s(x_1 +ε) + s(x_1) =ε_1’,$

$$$s(x_2 +ε) + s(x_2) =ε_2’,$

$$$s(x_3 +3ε) + s(x_3) =ε_3’,$

Byte $$$ε_0’, ε_1’, ε_2’, ε_3’$dimodifikasi oleh kesalahan berisi informasi tentang kunci tidak dikenal yang menghasilkan byte ini.



Semua persamaan tersebut dapat digeneralisasikan dalam satu persamaan

s (x + cε) + s (x) = ε ', (1)

dengan nilai konstanta =' 01 ',' 02 'atau' 03 'dan persamaan inilah yang akan kita selesaikan lebih lanjut dan menganalisa.



Definisi 1 . Himpunan solusi persamaan (1) untuk kesalahan ε dilambangkan dengan simbol B (cε ') dan ditentukan oleh pernyataan:

B (cε') = S (cε ') = {ε є GF [2 ⁸ ]: ∃ x є GF [2 ⁸ ], s (x + cε) + s (x) = ε '}, | B (cε') | = 127.



Ini adalah area kesalahan individu yang sesuai dengan kesalahan spesifik ε '. Untuk ε 'lainnya, area kesalahannya akan berbeda.



Definisi 2 . Pertimbangkan transformasi linier ℓ di atas bidang GF (2):

ℓ: GF [2 ⁸ ] → GF [2 ⁸ ];

x → x ² + x.



Citra ℓ merupakan pemetaan ruang vektor Im (ℓ) GF (2), yaitu, himpunan elemen

(x ² + x) dari GF [2 ⁸ ] kita nyatakan 1 = Im (ℓ) dan dimensinya dimGF (2) (E1) = 7. Jika θ є 1, maka ada dua solusi berbeda x1, x2 є GF [ 2 ⁸ ] persamaan x ² + x = θ, dan solusi memenuhi hubungan x2 = x1 + 1 dan x2 ∙ x1 = θ (modd φx, (2 ⁸ -1)) dengan teorema Vieta.



Variabel θ adalah



suku bebas dari persamaan kuadrat. Mari kita gambarkan transformasi linier yang dianggap dengan sebuah contoh.



Contoh Field GF diatur [2 ⁸], transformasi x → x ² + x dilakukan pada elemen-elemennya .



Tabel 8 - fragmen awal bidang GF [2 ⁸ ] dan hasil transformasi elemen.





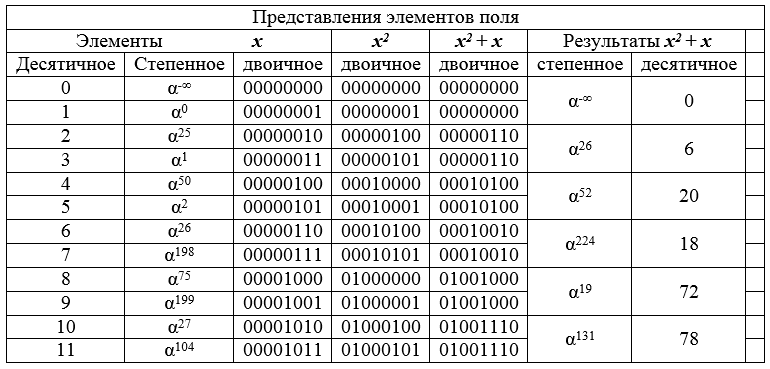
Tabel 8 menunjukkan bagaimana konversi mengubah pasangan yang berdekatan dalam daftar berurutan desimal ke elemen bidang yang sama. Oleh karena itu, hasil transformasi (gambar) adalah setengah dari preimage (bidang tersebut, seolah-olah, dikompresi oleh faktor 2). Prinsip kontraksi dimensi himpunan ini membentuk dasar dari serangan yang diusulkan.





Proposisi 2 . Pernyataan berikut berlaku untuk λ1, λ2 є GF [2 ⁸ ] - {0}:

2. Generalisasi dan implementasi

Pertama-tama, dengan bantuan aplikasi perangkat lunak khusus, 20 ciphertext dengan kesalahan dihasilkan. Untuk melakukan ini, teks sumber, kunci, kesalahan dimasukkan ke dalam model (program) dan nomor posisi diatur di mana kesalahan ditempatkan. Dengan menekan tombol "Start", program mengimplementasikan algoritma dan menampilkan hasil dari 2 putaran terakhir enkripsi dalam bentuk yang diperluas untuk teks dengan kesalahan, teks tanpa kesalahan, dan perbedaan di antara keduanya. Setelah itu, ciphertext disimpan tanpa kesalahan dan dengan kesalahan. Nilai kesalahan berubah secara siklis dan dengan menekan tombol "Start", ciphertext berikutnya dengan kesalahan diperoleh. Pada satu nilai kolom, 5 ciphertext dengan kesalahan terbentuk.



Untuk melakukan serangan, perlu untuk membuka file dengan ciphertext tanpa kesalahan dan ciphertext dengan kesalahan menggunakan program (data dalam file disajikan dalam bentuk heksadesimal), ciphertext dan perbedaannya ditampilkan sebagai array persegi byte (State). Menekan tombol "Search for key" memulai prosedur pencarian untuk kemungkinan byte dari kunci tersebut. Status proses saat ini ditampilkan dalam kotak teks. Setelah itu, ciphertext dengan kesalahan lain dibuka, dan prosedur diulangi. Ketika byte kunci bulat 10 diterima, itu juga muncul dalam array byte persegi yang sesuai. Saat menjalankan semua 20 ciphertext yang dihasilkan pada tahap sebelumnya dengan kesalahan, ada kemungkinan besar untuk mendapatkan nilai semua byte dari kunci putaran 10 (jika tidak, ciphertext dengan kesalahan juga diperlukan).Setelah itu, kembalikan kunci enkripsi sesuai dengan algoritma "Pemulihan kunci sandi menggunakan subkunci terakhir" yang diberikandisini .





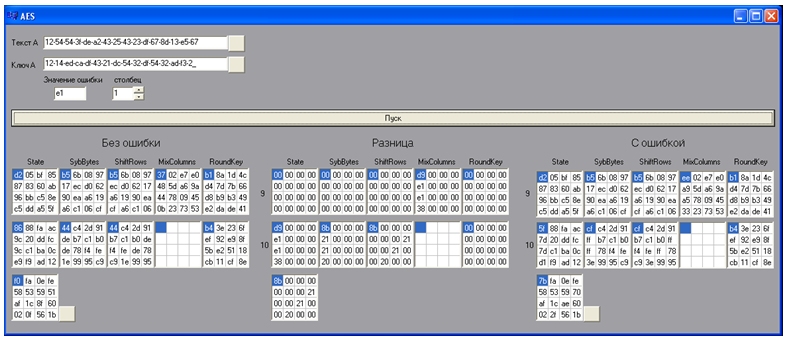
Gambar 11 - Produk perangkat lunak untuk membuat ciphertext dengan kesalahan



Untuk mempercepat prosedur pencacahan ciphertext dengan kesalahan, Anda dapat memberi tanda centang di depan tombol "Temukan kunci"





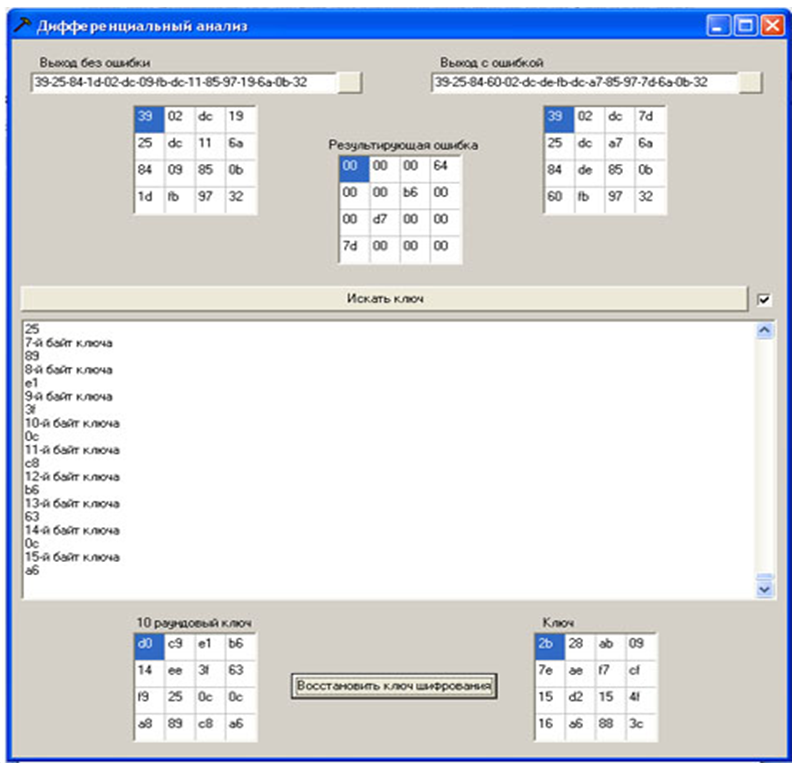
Gambar 12 - Implementasi perangkat lunak serangan



Contoh operasi produk perangkat lunak:



Kode sumber 3243f6a8885a308d313198a2e0370734

Key 2b7e151628aed2a6abf7158809cf4f3c

Error 1 1e000000000000000000000000000000

Ciphertext dengan error 1

Kemungkinan byte de25841d03bdc









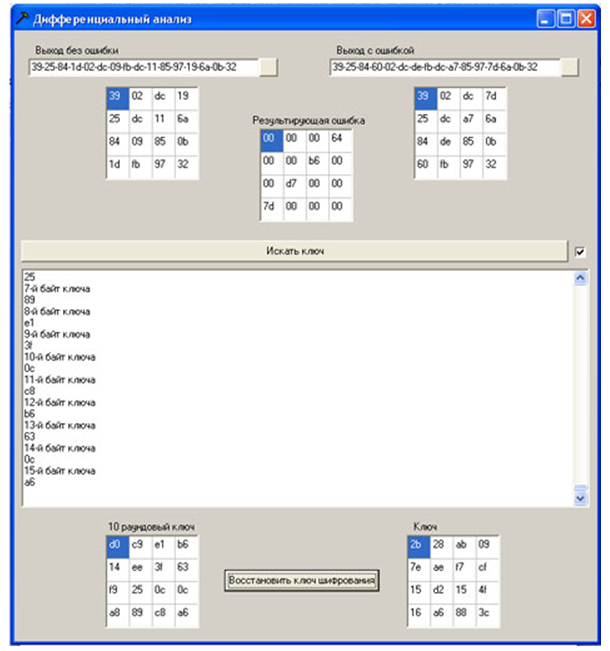
Gambar 13 - Contoh operasi program



Kunci putaran 10 d014f9a8c9ee2589e13f0cc8b6630ca6 telah dipulihkan sepenuhnya

Kunci yang dipulihkan 2b7e151628aed2a6abf7158809cf4f3c, seperti yang diharapkan, cocok dengan kunci yang ditentukan dalam sesi enkripsi.

2.1. Situasi ketika tidak ada informasi lokasi kesalahan

Pada titik ini, diasumsikan bahwa kesalahan terdapat dalam byte status antara dua eksekusi terakhir operasi MixColumns. Ini adalah kasus yang sama, kecuali fakta bahwa kesalahan dapat diapit antara byte dari 1 hingga 16. Kesalahan dikalikan dengan operasi MixColumns dan menyebar ke status 4 byte.



Kesalahan paksa dihasilkan di baris pertama dari matriks status diferensial. Di sini dimungkinkan untuk menentukan kolom mana yang memasukkan kesalahan dengan melihat kolom kesalahan paksa. Ini dilakukan dengan memeriksa empat kemungkinan posisi baris untuk kesalahan yang dimasukkan menggunakan metode yang dijelaskan dalam uraian sebelumnya.

2.2. Perangkat perangkat keras

Anggaplah Anda memiliki kemampuan untuk mengganggu perangkat keras AES secara fisik. Pertama, mari kita hitung sandi untuk lebih dari sepuluh teks biasa menggunakan perangkat AES. Kemudian kami mengubah proyek contoh dengan memotong garis dan menghubungkannya ke tanah (atau Vcc) sementara antara dua byte selama putaran, yang terletak dua putaran sebelum selesai. Bagaimanapun, kita memiliki byte di putaran Nk -2, selalu diganti dengan '00' (atau 'FF').



Kami menghitung waktu lain pesan yang sama dengan perangkat akting. Dengan teks biasa acak, byte yang rusak seperti kesalahan acak. Kesalahan tunggal ini diterjemahkan menjadi empat kesalahan di babak Nk -1 dan enam belas kesalahan di babak Nk. Dalam hal ini, matriks deviasi (diferensial) dapat diperoleh, dengan bantuan yang dimungkinkan, dengan menganalisis kesalahan, untuk menemukan kunci putaran terakhir.



Referensi:



[1] FIPS PUB 197: Standar Enkripsi Lanjutan, csrc.nist.gov/publications/fips/fips197/fips-197.pdf

[2] Boneh, DeMillo, dan Lipton, Tentang Pentingnya Memeriksa Protokol Kriptografi untuk Kesalahan, Catatan Kuliah dalam Ilmu Komputer, Kemajuan dalam Kriptologi, prosiding EU-ROCRYPT'97, hal. 37-51, 1997.

[3] E. Biham & A. Shamir, Analisis Kesalahan Diferensial dari Secret Key Cryptosystems, CS 0910, Prosiding Crypto'97.

[4] Ross J. Anderson, Markus G. Kuhn: Tamper Resistance - a Cautionary Note, The Second USENIX Workshop on Electronic Commerce Proceedings, Oakland, California, 18-21 November 1996, hlm 1-11, ISBN 1-880446- 83-9.