
Armoured Warfare: Project Armata adalah game aksi tank online gratis yang dikembangkan oleh Allods Team, studio game MY.GAMES. Terlepas dari kenyataan bahwa permainan dibuat di CryEngine, mesin yang cukup populer dengan render waktu nyata yang baik, untuk permainan kami, kami harus memodifikasi dan membuat banyak dari awal. Pada artikel ini, saya ingin berbicara tentang bagaimana kami menerapkan penyimpangan berwarna untuk tampilan orang pertama, dan apa itu.
Apa itu chromatic aberration?
Chromatic aberration adalah cacat lensa di mana tidak semua warna sampai pada titik yang sama. Ini disebabkan oleh fakta bahwa indeks bias medium tergantung pada panjang gelombang cahaya (lihat dispersi ). Sebagai contoh, ini adalah bagaimana situasi terlihat ketika lensa tidak menderita penyimpangan berwarna:
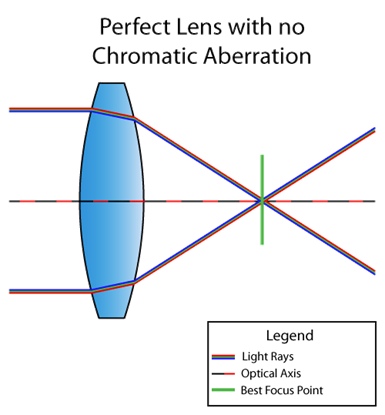
Dan ini adalah lensa dengan cacat:
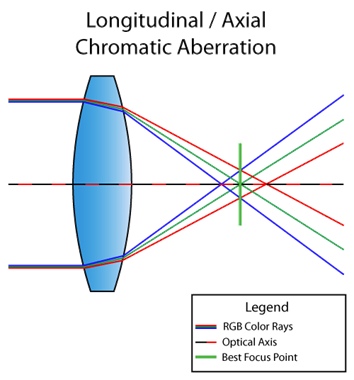
Omong-omong, situasi di atas disebut aberasi kromatik longitudinal (atau aksial). Ini terjadi ketika panjang gelombang yang berbeda tidak bertemu pada titik yang sama dalam bidang fokus setelah melewati lensa. Kemudian cacat terlihat di seluruh gambar:

Pada gambar di atas, Anda dapat melihat bahwa warna ungu dan hijau menonjol karena cacat. Tidak dapat melihat? Dan di foto ini?

Ada juga penyimpangan kromatik lateral (atau lateral). Ini terjadi ketika cahaya berada pada sudut lensa. Akibatnya, panjang gelombang cahaya yang berbeda bertemu pada titik yang berbeda di bidang fokus. Ini gambar yang bisa Anda pahami:
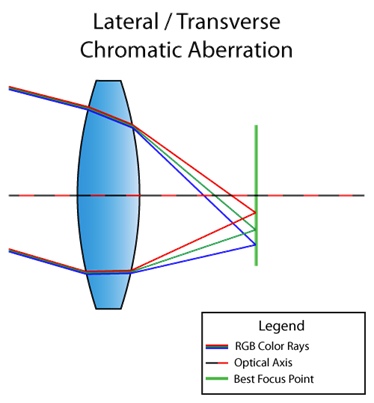
Anda sudah dapat melihat dari diagram bahwa sebagai hasilnya kita mendapatkan dekomposisi cahaya lengkap dari merah menjadi ungu. Tidak seperti longitudinal, aberasi kromatik lateral tidak pernah muncul di tengah, hanya lebih dekat ke tepi gambar. Agar Anda mengerti apa yang saya maksud, inilah gambar lain dari Internet:

Karena kita sudah selesai dengan teori, mari kita langsung ke intinya.
Aberasi kromatik lateral dengan dekomposisi ringan
Saya akan mulai dengan fakta bahwa saya akan menjawab pertanyaan yang bisa muncul di kepala banyak dari Anda: "Bukankah CryEngine menerapkan penyimpangan berwarna?" Ada. Tetapi ini digunakan pada tahap pasca-pemrosesan dalam shader yang sama dengan penajaman, dan algoritmenya terlihat seperti ini ( tautan ke kode ):
screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;Yang pada prinsipnya bekerja. Tapi kami punya permainan tentang tank. Kita membutuhkan efek ini hanya untuk pandangan orang pertama, dan hanya untuk kecantikan, yaitu, agar semuanya fokus di tengah (halo ke lateral aberration). Oleh karena itu, implementasi saat ini tidak sesuai setidaknya fakta bahwa efeknya terlihat di seluruh gambar.
Beginilah kelainan itu sendiri (perhatian ke sisi kiri):

Dan ini adalah tampilannya jika Anda memutar parameter:

Karena itu, kami telah menetapkan sebagai tujuan kami:
- Terapkan penyimpangan kromatik lateral sehingga semuanya dalam fokus dekat ruang lingkup, dan jika cacat warna karakteristik tidak terlihat di sisi, maka setidaknya menjadi kabur.
- Sampel tekstur dengan mengalikan saluran RGB dengan koefisien yang sesuai dengan panjang gelombang tertentu. Saya belum membicarakan hal ini, jadi sekarang mungkin tidak sepenuhnya jelas tentang poin ini. Tapi kami pasti akan mempertimbangkannya di semua detail nanti.
Pertama, mari kita lihat mekanisme dan kode umum untuk membuat penyimpangan kromatik lateral.
half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;
Jadi, pertama, topeng bundar dibangun, yang bertanggung jawab untuk jarak dari pusat layar, lalu arah dari pusat layar dihitung, dan kemudian semua ini dikalikan
blur. Blurdan falloff- ini adalah parameter yang dilewatkan dari luar dan hanya pengganda untuk menyesuaikan aberasi. Juga, parameter dilemparkan dari luar sampleCount, yang bertanggung jawab tidak hanya untuk jumlah sampel, tetapi juga, pada kenyataannya, untuk langkah antara titik pengambilan sampel, karena
half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);
Sekarang kita hanya perlu pergi
sampleCountsekali dari titik tertentu dari tekstur, bergeser setiap kali offsetDecrement, mengalikan saluran dengan bobot gelombang yang sesuai dan membaginya dengan jumlah bobot tersebut. Nah, ini saatnya berbicara tentang poin kedua dari tujuan global kita.
Spektrum cahaya yang terlihat berkisar antara 380 nm (violet) hingga 780 nm (merah). Dan lihat, panjang gelombang dapat dikonversi ke palet RGB. Dalam Python, kode yang melakukan sihir ini terlihat seperti ini:
def get_color(waveLength):
if waveLength >= 380 and waveLength < 440:
red = -(waveLength - 440.0) / (440.0 - 380.0)
green = 0.0
blue = 1.0
elif waveLength >= 440 and waveLength < 490:
red = 0.0
green = (waveLength - 440.0) / (490.0 - 440.0)
blue = 1.0
elif waveLength >= 490 and waveLength < 510:
red = 0.0
green = 1.0
blue = -(waveLength - 510.0) / (510.0 - 490.0)
elif waveLength >= 510 and waveLength < 580:
red = (waveLength - 510.0) / (580.0 - 510.0)
green = 1.0
blue = 0.0
elif waveLength >= 580 and waveLength < 645:
red = 1.0
green = -(waveLength - 645.0) / (645.0 - 580.0)
blue = 0.0
elif waveLength >= 645 and waveLength < 781:
red = 1.0
green = 0.0
blue = 0.0
else:
red = 0.0
green = 0.0
blue = 0.0
factor = 0.0
if waveLength >= 380 and waveLength < 420:
factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
elif waveLength >= 420 and waveLength < 701:
factor = 1.0
elif waveLength >= 701 and waveLength < 781:
factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
gamma = 0.80
R = (red * factor)**gamma if red > 0 else 0
G = (green * factor)**gamma if green > 0 else 0
B = (blue * factor)**gamma if blue > 0 else 0
return R, G, B
Hasilnya, kami mendapatkan distribusi warna berikut:

Singkatnya, grafik menunjukkan berapa banyak dan warna apa yang terkandung dalam gelombang dengan panjang tertentu. Pada sumbu ordinat, kita hanya mendapatkan bobot yang sama dengan yang saya bicarakan sebelumnya. Sekarang kita dapat sepenuhnya mengimplementasikan algoritma, dengan mempertimbangkan yang dinyatakan sebelumnya:
half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
for (int i = 0; i < sampleCount; i++)
{
waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
Weight.r = GetRedWeight(waveLength);
Weight.g = GetGreenWeight(waveLength);
Weight.b = GetBlueWeight(waveLength);
offset -= offsetDecrement;
color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
accumulator.rgb += color.rgb * Weight.rgb;
WeightSum.rgb += Weight.rgb;
}
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);
Artinya, idenya adalah bahwa semakin banyak yang kita miliki
sampleCount, semakin sedikit langkah yang kita miliki antara titik-titik sampel, dan semakin kita membubarkan cahaya (kita memperhitungkan lebih banyak gelombang dengan panjang yang berbeda).
Jika masih belum jelas, maka mari kita lihat di sebuah contoh spesifik, yaitu usaha pertama kami, dan saya akan menjelaskan apa untuk mengambil untuk
startWaveLengthdan endWaveLength, dan bagaimana fungsi akan dilaksanakan GetRed(Green, Blue)Weight.
Menyesuaikan seluruh spektrum yang terlihat
Jadi, dari grafik di atas, kita tahu perkiraan rasio dan nilai perkiraan palet RGB untuk setiap panjang gelombang. Misalnya, untuk panjang gelombang 380 nm (violet) (lihat grafik yang sama), kita melihat bahwa RGB (0,4, 0, 0,4). Nilai-nilai inilah yang kami ambil untuk bobot yang saya bicarakan sebelumnya.
Sekarang mari kita coba untuk menyingkirkan fungsi memperoleh warna dengan polinomial tingkat keempat sehingga kalkulasi lebih murah (kami bukan studio Pixar, tetapi studio game: semakin murah kalkulasi, semakin baik). Polinomial derajat keempat ini harus mendekati grafik yang dihasilkan. Untuk membangun polinomial, saya menggunakan perpustakaan SciPy:
wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)
Akibatnya, hasil berikut diperoleh (saya membagi menjadi 3 grafik terpisah yang sesuai dengan masing-masing saluran yang terpisah, sehingga lebih mudah untuk membandingkan dengan nilai yang tepat):
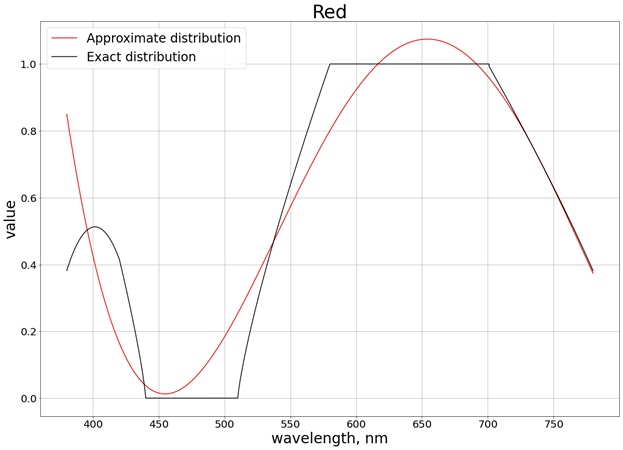
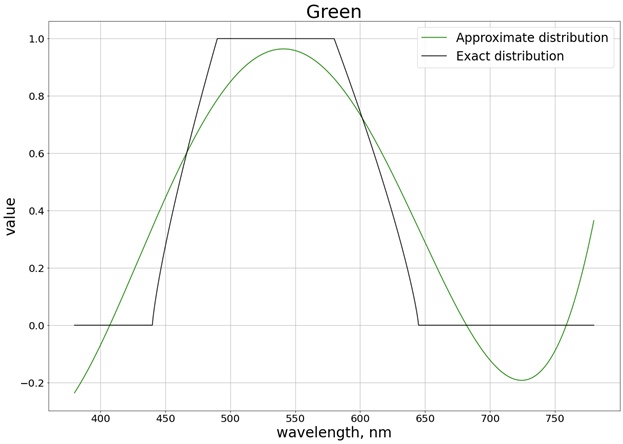
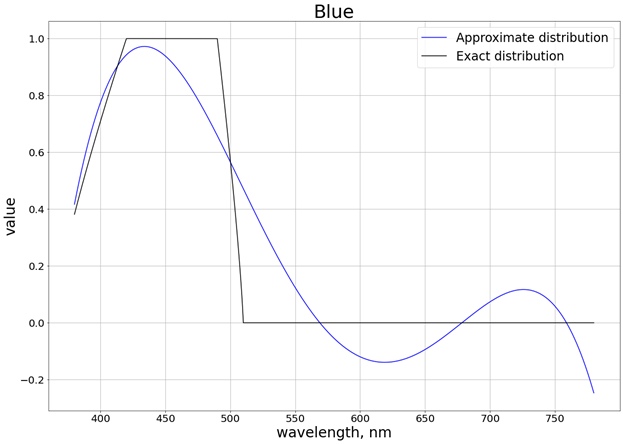
Untuk memastikan bahwa nilai tidak melampaui batas segmen [0, 1], kami menggunakan fungsi
saturate. Untuk merah, misalnya, fungsi diperoleh:
half GetRedWeight(half x)
{
return saturate(0.8004883122689207 +
1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) -
1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}
Parameter yang hilang
startWaveLengthdan endWaveLengthdalam hal ini adalah 780 nm dan 380 nm, masing-masing. Hasilnya dalam praktek sampleCount=3adalah sebagai berikut (lihat tepi gambar):

Jika kita mengubah nilainya, meningkat
sampleCountmenjadi 400, maka semuanya menjadi lebih baik:

Sayangnya, kami memiliki render waktu nyata di mana kami tidak dapat mengizinkan 400 sampel (sekitar 3-4) dalam satu shader. Oleh karena itu, kami sedikit mengurangi rentang panjang gelombang.
Bagian dari spektrum yang terlihat
Mari kita ambil rentang sehingga kita berakhir dengan warna merah murni dan biru murni. Kami juga menolak ekor merah di sebelah kiri, karena sangat mempengaruhi polinomial akhir. Hasilnya, kami mendapatkan distribusi di segmen [440, 670]:

Juga, tidak perlu melakukan interpolasi pada seluruh segmen, karena sekarang kita bisa mendapatkan polinomial hanya untuk segmen di mana nilainya berubah. Misalnya, untuk warna merah, ini adalah segmen [510, 580], di mana nilai bobot bervariasi dari 0 hingga 1. Dalam hal ini, Anda bisa mendapatkan polinomial orde kedua, yang kemudian
saturatejuga dikurangi oleh fungsi ke kisaran nilai [0, 1]. Untuk ketiga warna kami mendapatkan hasil berikut dengan saturasi diperhitungkan:

Sebagai hasilnya, kita mendapatkan, misalnya, polinomial untuk merah:
half GetRedWeight(half x)
{
return saturate(0.5764348105166407 +
0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) -
0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}
Dan dalam praktiknya dengan
sampleCount=3:

Dalam hal ini, dengan pengaturan bengkok, kira-kira hasil yang sama diperoleh seperti saat pengambilan sampel pada seluruh rentang spektrum yang terlihat:

Jadi, dengan polinomial derajat kedua, kami mendapatkan hasil yang baik dalam kisaran panjang gelombang dari 440 nm hingga 670 nm.
Optimasi
Selain mengoptimalkan perhitungan dengan polinomial, Anda dapat mengoptimalkan pekerjaan shader, bergantung pada mekanisme yang kami letakkan di dasar penyimpangan kromatik lateral kami, yaitu, tidak melakukan perhitungan di area di mana perpindahan total tidak melampaui piksel saat ini, jika tidak, kami akan mengambil sampel yang sama pixel, dan kami mendapatkannya.
Ini terlihat seperti ini:
bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
return OUT;
}
Optimalisasi kecil, tetapi sangat bangga.
Kesimpulan
Aberasi kromatik lateral itu sendiri terlihat sangat dingin, cacat ini tidak mengganggu penglihatan di tengah. Gagasan menguraikan cahaya menjadi bobot adalah percobaan yang sangat menarik yang dapat memberikan gambar yang sama sekali berbeda jika mesin atau game Anda memungkinkan lebih dari tiga sampel. Dalam kasus kami, dimungkinkan untuk tidak repot dan membuat algoritma yang berbeda, karena bahkan dengan optimasi kami tidak dapat membeli banyak sampel, dan, misalnya, antara 3 dan 5 sampel, perbedaannya tidak terlalu terlihat. Anda dapat bereksperimen dengan metode yang dijelaskan sendiri dan melihat hasilnya.