Model matematika dari fenomena tersebut mendalilkan bahwa semua proses berlangsung dalam ruang-waktu 4-dimensi, di mana fenomena SRT mengikuti dari pelestarian interval peristiwa selama transformasi rotasi sistem koordinat. Hampir tidak dapat disangkal bahwa kenyataan, seolah-olah, membentang di atas konstruksi matematika. Selain itu, fakta bahwa angka imajiner, dalam kenyataannya tak terbayangkan, memainkan peran yang hampir seluruhnya penting di dalamnya, tidak mengurangi keberhasilan sains. Bahkan E. Mach mengatakan bahwa penjelasan itu berlebihan jika fenomena yang diamati dijelaskan dengan baik oleh formula. Dan jangan berdebat dengan empirio-kritik ini.
Matematikawan menciptakan abstraksi dan mencobanya pada kenyataan. Karenanya Singularitas, lubang cacing dan hal-hal eksotis lainnya. Atau mungkin ada baiknya berfantasi , misalnya, tentang apa yang akan berubah dalam gagasan kita tentang dunia jika penyebab kontraksi Lorentz adalah beberapa mekanisme fisik yang diasumsikan secara hipotesis. Kenapa tidak?
1 penyebab fisik kontraksi Lorentz
Pertama, saya akan mengungkapkan pepatah yang nampak jelas bahwa partikel, atom, molekul berinteraksi satu sama lain melalui bidang fisik . Kita tentu saja dapat mengatakan bahwa mereka bertukar partikel kuantum, tetapi kita sekarang bermain di bidang teori relativistik, jadi untuk sekarang kita akan melupakan quanta. Jadi, asumsi fantastis pertama adalah bahwa justru karena penyeimbangan timbal balik antara efek medan, partikel-partikel ditambahkan ke konfigurasi tertentu dan membentuk badan . Jika beberapa partikel menyimpang dari posisi kesetimbangan, maka gangguan medan akan berlari darinya, yang akan memindahkan sisa partikel, yang, pada gilirannya, akan menyebabkan efek medan balik dari partikel-partikel tersebut pada partikel ini.
Dan asumsi kedua adalah itugangguan medan merambat di ruang bersama tertentu dengan kecepatan tertentu . Dan sifat yang fantastis dari asumsi ini adalah bahwa, menurut ilmu pengetahuan, bidang itu ada dengan sendirinya dalam ruang-waktu 4-dimensi (P-W) dan tidak tersebar pada apa pun. Secara umum, sulit dalam sains ... Kita akan berasumsi bahwa medan tersebar dan ada dalam ruang 3 dimensi tunggal - di mana kita berada, Bumi dan bintang-bintang. Tampaknya ini tidak perlu dikatakan dan siapa yang tidak tahu, tetapi mari kita lihat apa yang terjadi. Mereka yang tidak tertarik dengan formula dapat membatasi diri hanya membaca teks yang dipilih.
Jadi, kami sepakat bahwa ada waktu interaksi antara partikel, yang terdiri dari waktu kedatangan kemarahan kepada mereka dan waktu kembalinya respon dari mereka kembali. Akibatnya, konfigurasi bodi sebelumnya secara bertahap akan dibangun kembali. Gbr.1 Pengaruh medan yang menentukan posisi partikel
Untuk setiap titik tubuh, dimungkinkan untuk membedakan kelompok titik yang akan memiliki waktu interaksi yang sama dan yang akan kita sebut isokron dengan titik ini. Situasi ini tercermin pada Gambar. 1. Tentu saja, pada saat diam, bola dari jari-jari istirahat R di sekitar titik adalah titik titik (GMT) yang cocok dengannya.
Perhatikan bahwa gerakan suatu partikel pada setiap momen ditentukan oleh jumlah gaya resultan yang diterapkan secara bersamaan dari totalitas semua kelompok partikel yang isokron dengannya.... Mari kita coba mencari tahu bagaimana permukaan GMT, yang dibentuk oleh serangkaian poin 2, 3, dll., Akan berubah ketika tubuh bergerak. dengan waktu interaksi yang sama dengan poin 1, yang mungkin tidak lagi menjadi bola.
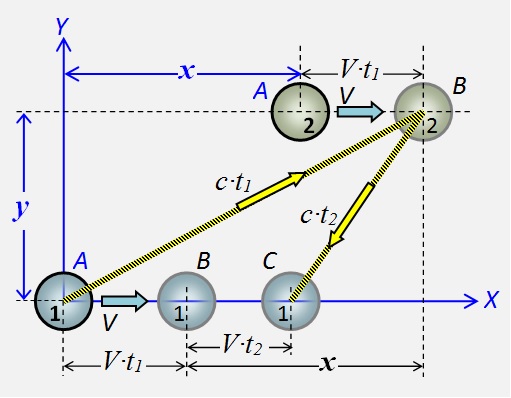Mari titik-titik tubuh 1 dan 2 tetap saling dan serempak bergerak kanan dengan kecepatan V . Ketika salah satu titik di asal, bidang gangguan dikirim ke titik 2. saling susunan titik-titik yang ditandai dengan huruf A . Gbr.2 Skema interaksi lapangan dari titik-titik tubuh - bolak-balik
Ketika gangguan mencapai titik 2, itu akan menempuh jarak V ∙ t 1 . Posisi ditandai poin dengan huruf B . Selama gangguan kembali dari titik 2 ke titik 1, titik 2 akan mencakup jarakV ∙ t 2 . Posisi baru mereka ditandai dengan C .
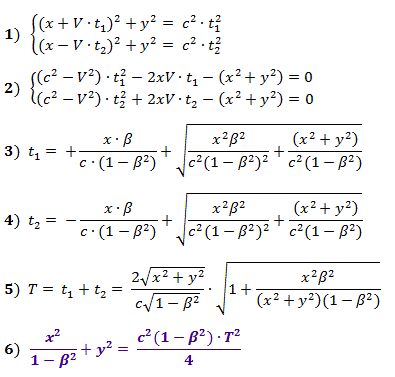Rumus (1), menurut teorema Pythagoras, menggambarkan jarak pada Gambar. 2, dan yang diperoleh dari mereka (2) adalah persamaan untuk menghitung kali t 1 dan t 2 , nilai-nilai yang diberikan oleh rumus (3) dan (4) untuk nilai positif dari akar, di mana β = V / c .
Formula (5) memberikan nilai waktu interaksi dari mengirim gangguan hingga menerima respons.
Dari (5) kita memperoleh persamaan (6) untuk koordinat x dan y dari tempat geometrik titik isokron dengan waktu interaksi titik 1 adalah sama.
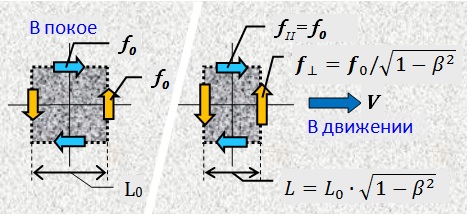
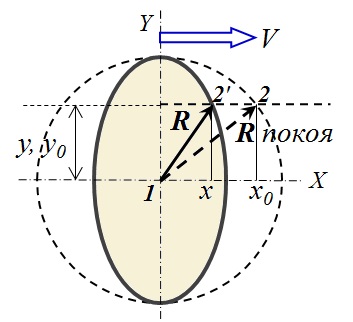Formula (6) menggambarkan ellipsoid yang ditunjukkan pada Gambar. 3, dikompresi sepanjang arah gerakan (sepanjang sumbu X) oleh √ (1 - β 2 ) kali, yaitu, menurut rumus Lorentz. Titik 2 pada permukaan bola saat diam, sambil bergerak, akan bergerak ke posisi 2 ' . Dalam hal ini, titik material yang isokron dengan titik 1 saat diam akan tetap isokron selama gerakan . Gbr.3
Jadi, ketika bergerak, objek material dikompresi menurut Lorentz justru karena "gambar" medan fisik terkompresi, yang memastikan integritasnya dalam ruang .
Karena kontraksi Lorentz adalah sama untuk semua titik isochronous yang mengelilingi setiap titik objek, maka seluruh objek yang bergerak akan berkontraksi secara proporsional sepanjang sumbu gerak.
2. Penurunan formula untuk pelebaran waktu
Mari kita tentukan waktu interaksi ketika objek bergerak dibandingkan dengan waktu interaksi saat istirahat.
Rumus (7) menghubungkan koordinat titik selama gerakan dengan koordinatnya diam sesuai dengan
persamaan (6). Rumus (8) menghitung waktu interaksi saat istirahat. Rumus (9) dan (10) diperoleh dari rumus (6) dengan mensubstitusi nilai koordinat x dan y dan R sisanya dari rumus (7). Formula (11) setara dengan (10). Formula (12), diperoleh dari (11) dengan mengganti sisi kiri formula (8) ke dalamnya, menghubungkan waktu interaksi saat istirahat dan selama gerakan. Dalam bentuk tradisional, ini tercermin dalam rumus (13), di mana T 0 adalah interval waktu antara peristiwa dalam objek istirahat, danT adalah interval waktu antara peristiwa yang sama dalam benda bergerak.
Jadi, waktu interaksi semua titik dalam objek bergerak meningkat dalam proporsi yang sama menurut Lorentz dibandingkan dengan waktu interaksi saat istirahat. Dengan demikian, secara umum, semua proses dalam objek yang bergerak sebenarnya melambat dalam hal yang sama .
Alasan perlambatan waktu mudah dipahami jika kita memperhitungkan bahwa gangguan medan dari bagian belakang partikel yang berinteraksi harus mengejar ketinggalan dengan bagian depan dalam arah gerakan . Ketika kecepatan tubuh hampir sama dengan kecepatan cahaya, akan butuh waktu lama untuk mengejar ketinggalan, dan jika kecepatan tubuh sama dengan kecepatan cahaya, itu tidak akan pernah mengejar. Semua perubahan dalam tubuh akan berhenti dan waktu di dalamnya akan berhenti.
3. Penjelasan fenomena kekonstanan kecepatan cahaya, dll.
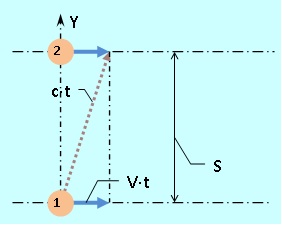
Mari kita lakukan eksperimen pemikiran. Biarkan denyut cahaya dipancarkan dari mobil terakhir kereta, yang diterima di kepala mobilnya. Kita harus mengukur waktu T 0 yang akan dihabiskan cahaya pada lintasan kereta yang dikenal panjang L 0 dalam sistemnya sendiri. Sebagai buktinya, kami akan menggunakan asumsi tentang homogenitas dan isotropi ruang, khususnya, kami akan mengasumsikan hasil pengukuran yang sama untuk paruh pertama dan kedua kereta, serta untuk arah maju dan mundur. Tetapi, sebenarnya, asumsi ini hanya berlaku di dalam lokasi dan waktu percobaan.
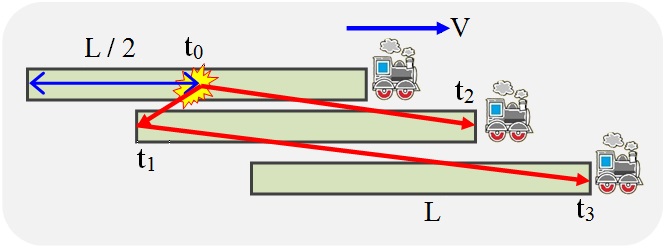
Fig. 4. Eksperimen pemikiran untuk menentukan kecepatan cahaya dalam kereta yang bergerak
Untuk menyinkronkan saat mengirim sinyal dari mobil terakhir kereta dan awal penghitung waktu di mobil depannya, kami menggunakan pulsa cahaya mulai dari tengah kereta ke kedua ujungnya.
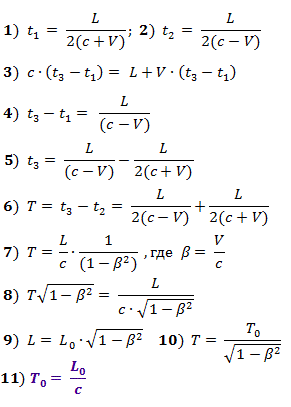
Ketika sinyal awal dari tengah kereta mencapai ekornya (waktu t 1 ), pulsa cahaya akan dikirim. Ketika sinyal mulai mencapai kepala kereta (waktu t 2 ), hitungan mundur akan dimulai sampai kedatangan pulsa yang dikirim.
Ketika cahaya bergerak ke ekor, kecepatannya ditambahkan ke kecepatan kereta, ketika ke kepala, kecepatan kereta dikurangi. Kami mendapatkan hubungan yang diberikan di bawah ini dalam rumus (1) - (6).
Waktu T = t 3 - t 2 adalah interval waktu, yang,menurut pengamat di kereta , ia memisahkan peristiwa saat mengirim sinyal dari ujung kereta (dari saat menerima sinyal awal di sana) dan saat penerimaannya di kepala kereta.
Dari (6) kita memperoleh rumus (7), yang kita ubah ke bentuk (8). Selanjutnya, kita akan memperhitungkan bahwa semua kuantitas L , T dan t di sini diukur dalam kerangka referensi dari pengamat luar dalam ruang di mana eksperimen pemikiran berlangsung. Tetapi ketika sebuah benda bergerak di ruang angkasa, panjangnya, sebagaimana dibuktikan pada Bab 1 , sebenarnya mengalami kontraksi Lorentz, dan waktu peristiwa, sebagaimana dibuktikan pada Bab 2, sebenarnya melambat dengan jumlah yang sama, yaitu melanjutkan lebih lama daripada saat istirahat, yang tercermin dalam rumus (9) dan (10). Mengganti rasio ini menjadi formula (8) untuk interval T - waktu tempuh cahaya dari ekor ke kepala kereta, kita mendapatkan hubungan (11).
Tetapi hubungan apa yang dimiliki T 0 dan L 0 ini saat istirahat dengan waktu dan panjangnya sendiri untuk peristiwa yang sama, diukur dalam kerangka acuan inersia (IRF) yang terkait dengan kereta yang bergerak? Jelas mereka setara . Faktanya adalah bahwa waktu dan panjang dinyatakan secara numerik melalui hubungannya dengan standar. Dengan demikian, pengukuran koordinat temporal dan spasial dari sesuatu yang dilakukan saat diam akan secara numeriksama dengan pengukuran yang sama, dibuat dalam ISO bergerak, karena ketika memindahkan nilai pengukuran dan standar akan berubah secara proporsional.
Pertanyaannya adalah bagaimana tepatnya mereka berubah ketika bergerak di ruang angkasa. Eksperimen pikiran dengan kereta membuktikan bahwa mereka berubah sedemikian rupa sehingga nilai numerik dari kecepatan cahaya yang diukur dalam IFR tetap sama dengan nilai kecepatannya di ruang angkasa . Inilah tepatnya yang bukan bukti apriori yang jelas dan diperlukan.
Kita melihat bahwa "dalil tentang kekonstanan kecepatan cahaya" berasal dari fakta kontraksi Lorentz sendiri, yang secara matematis berasal dari ketergantungan lokasi materi materi pada kecepatan perambatan dan konfigurasi medan fisik dalam ruang .
Untuk melengkapi gambar, kami juga menentukan kecepatan cahaya melintasi pergerakan kereta, misalnya, antara dinding kereta pada jarak S 0 dari satu sama lain. Untuk melakukan ini, kami mengukur waktu pergerakan pulsa cahaya ( 2 · t 0 ) bolak-balik. Mengingat simetri yang jelas "di sana" dan "kembali" kita akan mempertimbangkan hanya "di sana". Dalam sistem pengamat luar, gerakan di ruang terjadi seperti yang ditunjukkan pada Gambar. 5.
Karenanya kita memiliki (c · t) 2 = S 2 + (V · t) 2 , di mana kita memperoleh t = S / (c · √ (1 - β²)) , di mana β = V / c .
Dalam sistem kereta, waktu yang tepat berlalu t 0terhubung dengan waktu yang berlalu di ruang oleh hubungan t = t 0 / (√ (1 - β²)) . Mengganti ungkapan ini ke dalam rumus untuk t dalam ruang, kita mendapatkan t 0 = S / c .
Fig. 5. Eksperimen pemikiran untuk menentukan kecepatan cahaya dalam kereta yang bergerak /
Dalam sistem kereta itu sendiri untuk t 0 yang sama , kita memiliki hubungan t 0 = S 0 / c 0 . Tetapi karena dimensi transversal tidak berubah selama gerakan, mis. S = S 0 , kita dapatkan bahwa c 0 = c .
Saya kira tidak perlu untuk membuktikan keteguhan kecepatan cahaya yang diukur untuk orientasi sinar yang sewenang-wenang, yang hanya akan menambah kompleksitas yang tidak perlu. Mempertimbangkan invariansi kecepatan cahaya yang terbukti, mudah untuk mendapatkan transformasi Lorentz (L), dan tanpa menarik persamaan Maxwell atau ke ruang Minkowski yang abstrak secara matematis.
4. Penurunan transformasi Lorentz
Acara terdiri dari kedatangan pulsa cahaya di titik " E ", yang
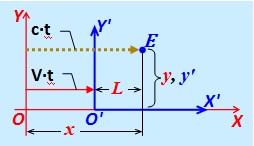terletak di koordinat tidak berubah x ' dan y' dalam sistem referensi {X ', Y'}, bergerak dengan kecepatan V relatif terhadap IFR tetap {X, Y}, dikirim pada saat ketika poin O dan O 'dari kedua CO bertepatan. Fig. 6.
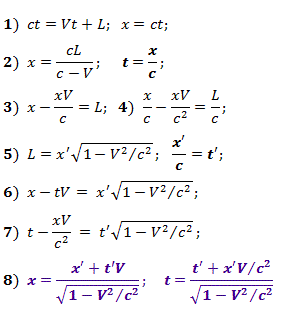Dalam panjang CO {X ', Y'} L , yang diukur dalam CO {X, Y}, koordinat x ' akan sesuai . Untuk kejadian tersebut, sistem persamaan (1) valid, penyelesaian yang kita peroleh (2), dan kemudian (3) dan (4).
Karena panjang benda yang bergerak dikompresi menurut Lorentz, dan kecepatan cahaya, sebagaimana dibuktikan dalam Bab 3 , sama di semua FR, maka untuk x yang tepatdant ' dalam hubungan {X', Y '} (5) valid. Mengganti relasi dari (5) menjadi (3) kita memperoleh (6), dan menggantikannya menjadi (4), kita memperoleh (7). Berdasarkan relativitas gerak, kita dapat mempertimbangkan sistem gerak {X, Y}, tetapi kemudian pada (6) dan (7) perlu untuk mengganti variabel tidak diarsir dengan yang diarsir, dan kecepatan V harus diambil dengan tanda yang berlawanan, atau hanya menyelesaikan sistem sehubungan dengan x dan t .
Sebagai hasilnya, kami memperoleh ekspresi (8) untuk bentuk kanonik dari transformasi Lorentz dari koordinat dan waktu kejadian dalam IFR yang berbeda.
Ketika menggunakan PL sebagai metode matematika formal murni, mekanisme fisik fenomena SRT tetap tidak terwujud. Oleh karena itu, dalam artikel saya sebelumnya tentang efek Doppler relativistikdanpenyimpangan cahaya , serta hukum refleksi dari cermin cenderung bergerak , SLs pada prinsipnya tidak digunakan untuk menunjukkan alasan fisik untuk fenomena ini.
5. Justifikasi prinsip relativitas dan batasan penerapannya
Perhatikan bahwa jika diam dalam diagram pada Gambar. 1 gangguan dari titik 1 ke GMT dari titik isochronous dengan itu datang secara bersamaan, maka ketika bergerak, dalam diagram pada Gambar. 2, ini tidak lagi terpenuhi. Pada setiap titik GMT ini, respons terhadap gangguan akan dibuat pada waktu yang berbeda, tetapi mereka akan bertemu pada titik 1 secara bersamaan . Pertanyaannya adalah, apakah hasilnya akan sama dengan saat istirahat?
Telah dibuktikan di atas bahwa dalam IFR apa pun, waktu dan jarak yang tepat yang diukur antara semua titik akan sama dengan saat istirahat . Akibatnya, jumlah periode, misalnya, dimulaigelombang elektromagnetik antara titik mana pun akan sama dengan saat istirahat. Karena perturbasi bidang konfigurasi sewenang-wenang dapat diwakili oleh ekspansi dalam serangkaian harmonik monokromatik, konfigurasi dan intensitas semua bidang dalam sistem intrinsik masing-masing akan sama saat diam. Akibatnya, hubungan fase dan sinkronisasi bidang yang membentuk tubuh tidak dilanggar, dan semua proses di dalamnya akan berjalan seperti saat istirahat.
Inilah yang dinyatakan oleh "prinsip relativitas" Einstein, dan, seperti yang kita lihat, secara matematis disimpulkan dari dua asumsi (lihat Bab 1), izinkan saya mengingatkan Anda: pertama : bahwa posisi partikel nyata ditentukan oleh struktur medan , dan kedua , bahwapropagasi bidang terjadi pada kecepatan yang terbatas .
Artinya, prinsip relativitas sudah, seolah-olah, bukan apriori prinsip universal , tetapi konsekuensi, dan memiliki batas penerapan yang jelas . Secara khusus, kecepatan cahaya tidak memiliki arti dari sebuah konstanta dunia, tetapi adalah kecepatan cahaya tertentu di wilayah ruang tertentu . Dan di beberapa tempat mungkin berbeda karena interaksi dengan bidang fisik setempat, misalnya, gravitasi. Jadi, kami memiliki dua alternatif yang menghasilkan formula relativistik yang persis sama:
- pertama, ortodoks dan ilmiah: ia membutuhkan postulat prinsip relativitas sejati yang apriori ;
- : ,
Dalam kasus pertama, fenomena SRT tidak memerlukan penjelasan, dan penyebab serta mekanismenya tetap tidak diketahui. Pertanyaan "mengapa?" bahkan ternyata di luar sains.
Dalam yang kedua , asumsi-asumsi itu bahkan cukup logis dan tidak ada yang perlu dipostulatkan, dan mereka "fantastis" hanya sejauh alasan-alasan lain untuk relativisme diterima dalam sains. Untuk pertanyaan "mengapa fenomena SRT seperti ini?" di sini penjelasan yang jelas dan bahkan hampir sepele diberikan. Tetapi ada kebutuhan mendesak untuk mengetahui sifat materi dan dalam hubungan apa dengan bidang fisik.
Karena itu, kami akan terus berfantasi lebih lanjut.
6. Penurunan rumus E = Mc² dan persamaan dinamika
Pertama, mari kita cari tahu bagaimana kekuatan ditransformasikan pada kecepatan relativistik. Mari kita pilih elemen volume di dalam tubuh di mana momen gaya aksi yang seimbang. Ketika tubuh bergerak, ukuran memanjang (sepanjang lintasan gerak) dari elemen yang dipilih
akan berkurang sesuai dengan koefisien Lorentz. Agar elemen tetap seimbang, gaya yang tegak lurus terhadap gerakan harus meningkat dalam rasio yang persis sama. Gbr. 7.
Besarnya gaya yang paralel dengan gerakan tidak akan berubah. Faktor ketergantungan gaya pada orientasi relatif terhadap arah gerak harus diperhitungkan dalam perluasan vektor gaya dalam rumus berikut.
Perhatikan bahwa akselerasi tubuh ke kecepatan tertentu dilakukan oleh kekuatan yang diberikan, yang, dengan demikian, melakukan beberapa pekerjaan, sehingga meningkatkan energi tubuh. DANApa perbedaan antara benda yang terdispersi dalam ruang dan benda yang diam? Fakta bahwa overclock dikompresi menurut Lorentz . Dalam Bab 1, rumus diturunkan untuk lokus poin (GMT) yang mengelilingi titik tertentu, dari mana mereka memiliki waktu interaksi yang sama dari bidang fisik. GMT ini ternyata merupakan ellipsoid yang dikompresi menurut Lorentz ke arah gerakan. Mari kita perhatikan fakta bahwa volume W ellipsoid ini menurun secara proporsional dengan kontraksi Lorentz. Ini tercermin dalam rumus (1) di bawah ini. Sekarang mari kita membuat asumsi yang sangat fantastis bahwa ketika sebuah benda dipercepat, kerja kekuatan dihabiskan untuk mengompresi volume ruang yang ditempati, yang kemudian tetap tidak berubah dalam gerakan bebas. Setidaknya, anggapan ini tidak lebih buruk dari pepatah ilmiah bahwa ruang dapat menekuk atau membengkak.
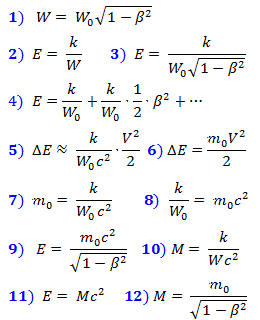Misalkan energi E ini berbanding terbalik dengan volume yang memungkinkan untuk mengompresnya sesuai dengan rumus (2), atau (3) setelah mengganti (1) ke dalamnya.
Kami memperluas E dari (3) menjadi deret Taylor (4), di mana (5) adalah kenaikan energi dari kecepatan dalam pendekatan pertama pada kecepatan rendah. Tetapi pada kecepatan rendah itu juga sama dengan (6). Membandingkan (5) dan (6), kita memperoleh (7) dan (8). Mengganti (8) menjadi (3), kita memperoleh (9), yang menghubungkan energi tubuh dalam ruang terkompresi dengan massa sisanya.
Mari kita ungkapkan massa relativistik dengan rumus (10), dari mana, gantikan (2), kita memperoleh ungkapan yang terkenal (11), yang menghubungkan massa dan energi. Membandingkan (9) dan (11), kami memperoleh (12).
Massa hanyalah formulasi energi yang dikeluarkan dalam ruang kompresi. Dan dalam hal ini mereka setara. Dan substansi hanya "menandai" area ruang yang ditempati oleh tubuh.
Perubahan energi total E sistem, mis. energi kompresi ruang, sesuai sepenuhnya dengan mekanika klasik Newton, sama dengan kerja gaya yang diterapkan sebagai produk gaya per jalur, dan perubahan dalam momentum P sistem sama dengan produk gaya yang sama dan waktu aksinya. Ketergantungan ini tercermin dalam formula (13). Setelah menggantikan mereka ekspresi untuk energi dari (11) dan momentum Pdari rumus (14)
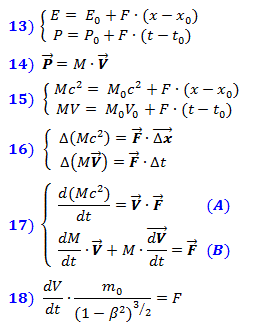kita memperoleh sistem persamaan (15), yang ditulis dalam bentuk kenaikan kecil dalam (16) dalam bentuk vektor. Kemudian, dengan membedakan sehubungan dengan waktu, kami menuliskan sistem persamaan diferensial (17) yang menggambarkan dinamika relativistik. Gaya F tidak perlu dibedakan, karena bersifat eksternal dan tidak bergantung pada variasi variabel sistem. Mengganti ekspresi untuk massa dari (12) menjadi rumus ( A ), kami memperoleh rumus relativistik terkenal untuk gerak bujursangkar (18). 
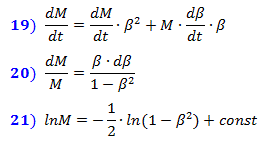Dari sistem persamaan (17) dimungkinkan untuk mengetahui ketergantungan massa pada kecepatan. Mengganti F dari formula ( B ) menjadi formula ( A ) dan membagi kedua sisi persamaan dengan c², ketika berakselerasi di sepanjang lintasan gerak, kita memperoleh ekspresi (19) dan (20). Dari mana, berintegrasi, kita memperoleh ekspresi (21). Sangat mudah untuk melihat bahwa itu adalah setara dengan ekspresi logaritmik (12) untuk massa relativistik, di mana const sama dengan logaritma dari sisa massa m 0 . Ini berarti bahwa hanya ketergantungan massa pada kecepatan memastikan korespondensi energi Mc² dan momentum M · V , dalam formula (16, 17). Dan dari sini juga mengikuti bahwa nilai yang sebelumnya kita anggap sebagai massa diam adalah konstan bebas dari kecepatan, seperti yang tertulis dalam rumus asli (9). Dan itu berarti asumsi kami tentang ketergantungan energi pada tingkat kompresi ruang adalah benar.
Tentu saja, klaim kompresi ruang tidak terlalu meyakinkan. Jika ruang seharusnya menjadi wadah kosong partikel dan benda, lalu bagaimana Anda bisa mengompres kekosongan? Kekosongan akan tetap kosong. Ilmu pengetahuan, bagaimanapun, memungkinkan dirinya untuk berbicara tentang kelengkungan ruang kosong - formula mengharuskannya. Namun, sebenarnya, ruangnya adalah abstraksi matematis.
Tetapi kita dapat mengasumsikan bahwa ruang tidak kosong, tetapi diisi dengan beberapa jenis materi , yang, anggaplah, tidak dalam keadaan terkompresi, dianggap oleh kita sebagai kekosongan... Misalnya, ketika berada di bawah tekanan kompresi, kami memiliki partikel dan benda material. Ketika ini diam di dalamnya, tingkat kompresi (energi) dari bagian ini sesuai dengan massa tubuh, dan dengan akselerasi, tingkat kompresi (energi) tubuh dan peningkatan massa yang sesuai.
Dan dalam lingkungan material ini, bidang fisik yang menentukan lokasi dan interaksi partikel (hingga yang primer "sangat-sangat" - yang, kami terus berfantasi , akan berubah menjadi fenomena bidang fokus dari lingkungan mereka yang tanpanya tidak ada), mungkin ada dan menyebar dengan kecepatan tertentu ), sisa dan energi gerak yang ditentukan oleh tingkat kompresi area materi utama yang ditempati oleh mereka . Sebenarnya,persamaan dari dinamika relativistik hanya menggambarkan gerakan dari ketidakhomogenan stres (badan material) dalam materi utama . Seperti yang bisa kita lihat, tidak ada kontradiksi dengan percobaan Michelson dan transformasi Lorentz.