Joshua Green dan Andrew Lobb, bosan karantina, menemukan cara untuk membuktikan salah satu varian dari teorema pasak persegi panjang

Dapatkah semua jenis persegi panjang ditemukan dalam loop tertutup?
Pada pertengahan Maret, matematikawan Joshua Green dan Andrew Lobb menemukan diri mereka dalam posisi yang sama - terkunci dalam empat dinding, mencoba beradaptasi dengan epidemi virus corona yang berkembang. Mereka memutuskan untuk mengatasinya dengan menyelidiki penelitian mereka.
"Saya pikir pandemi adalah semacam katalis untuk proses ini," kata Greene, seorang profesor di Boston College. "Kami memutuskan bahwa akan lebih baik untuk melakukan semacam kerja sama yang dapat mendukung kami."
Salah satu masalah yang dipecahkan oleh kedua sahabat itu adalah varian dari pertanyaan geometris yang tetap tidak terjawab selama lebih dari seratus tahun.
"Tugas ini sangat sederhana untuk dirumuskan dan dipahami, tetapi sangat sulit untuk diselesaikan," - kataElizabeth Denn dari Washington dan Lee University.
Semuanya dimulai dengan loop tertutup - setiap jalur lengkung yang memiliki awal dan akhir yang sama. Tugas yang diambil Green dan Lobb pada dasarnya mengemukakan bahwa dalam setiap jalan seperti itu ada set empat titik yang membentuk simpul-simpul persegi panjang dari proporsi tertentu.
Dan sementara "masalah pasak segi empat" ini terdengar seperti pertanyaan yang dapat diatasi oleh siswa sekolah menengah dengan penggaris dan kompas, ia telah menentang upaya matematikawan yang paling gigih selama beberapa dekade. Dan ketika Green dan Lobb mengambil alih, mereka tidak punya alasan untuk mengharapkan yang lain.
Greene mengatakan bahwa dari semua proyek sulit yang dikerjakannya, "yang ini menurut saya paling tidak menjanjikan."
Tapi pandemi itu berkembang, dan Green dan Lobb, yang bekerja di Durham University di Inggris dan Okinawa Institute of Science and Technology, masing-masing, melakukan percakapan Zoom mingguan dan dengan cepat melahirkan beberapa ide. Dan kemudian pada 19 Mei, ketika banyak bagian dunia dibuka kembali, mereka menerbitkan keputusan mereka .
Bukti terakhir mereka, yang menunjukkan bahwa persegi panjang memang dapat ditemukan, membawa masalah ini ke tingkat geometris yang sama sekali berbeda. Dan di sana pertanyaan keras kepala ini sangat mudah diterima.
"Ini sangat aneh," kata Richard Schwartz dari Brown University. "Gagasan ini sempurna untuk tugas ini."
Memikirkan kembali persegi panjang
Masalah pasak persegi panjang terkait erat dengan pertanyaan yang diajukan oleh ahli matematika Jerman Otto Töplitz pada tahun 1911. Dia memperkirakan bahwa pada kurva tertutup Anda dapat menemukan empat titik, yang menghubungkan Anda bisa mendapatkan persegi. Pertanyaannya tentang "pasak persegi" ini tetap terbuka.
"Ini adalah tugas lama dan membuat frustrasi yang tidak bisa diretas dengan cara apa pun," kata Green.
Untuk memahami kompleksitas masalah, penting untuk mengetahui sifat-sifat kurva yang dianggap dalam masalah pasak persegi - ini juga penting untuk bukti Green dan Lobb.
Pasangan ini memecahkan masalah untuk kurva tertutup, baik "terus menerus" dan "halus". Kontinuitas berarti tidak ada jeda. Kelancaran berarti kontinuitas dan tanpa sudut. Anda cenderung menggambar kurva yang mulus dan kontinu jika Anda duduk di meja dengan kertas dan pensil. Mereka "lebih mudah diajak bekerja sama," kata Green.
Kurva kontinu halus berbeda dari kurva kontinu sederhana, tetapi tidak mulus, seperti yang terlibat dalam dugaan Toeplitz pada pasak persegi. Kurva seperti itu dapat memiliki sudut - titik di mana kurva tiba-tiba menyimpang dan bergerak ke arah yang berbeda. Salah satu contoh utama dari kurva dengan banyak sudut adalah kurva Koch fraktal seperti kepingan salju ., pada kenyataannya, terdiri dari beberapa sudut. Kepingan salju Koch dan kurva serupa lainnya tidak dapat dianalisis menggunakan metode aljabar, yang membuatnya sangat sulit untuk dipelajari.
"Beberapa kurva kontinyu [tidak mulus] hanya menjijikkan," kata Denn.
Namun, masalah yang dipecahkan oleh Green dan Lobb adalah milik kurva halus dan, oleh karena itu, terus menerus. Dan alih-alih mencari tahu apakah selalu ada empat poin pada kurva seperti itu yang membentuk bujur sangkar - untuk kurva kontinu yang mulus, masalah ini diselesaikan pada tahun 1929 - mereka mempelajari sesuatu yang lain: apakah selalu ada empat poin pada kurva seperti itu yang membentuk persegi panjang dari angka yang diberikan proporsi, yaitu dengan rasio aspek apa pun. Untuk kotak, rasio ini adalah 1: 1, untuk TV definisi tinggi - 16: 9.

Terobosan besar pertama dalam masalah pasak segi empat datang dalam bukti yang ditemukan pada akhir 1970-an oleh Herbert Vaughn. Ini menawarkan cara baru dalam memandang geometri persegi panjang dan menyediakan beberapa metode yang kemudian digunakan oleh matematikawan lain, termasuk Green dan Lobb.
"Semua orang tahu bukti ini," kata Green. "Ini hampir folkloric, kamu belajar tentang hal-hal seperti itu dengan mendiskusikan semuanya di meja makan."
Alih-alih membayangkan persegi panjang sebagai empat titik yang terhubung, Vaughn membayangkannya sebagai dua pasang titik dalam hubungan satu sama lain.

Bayangkan sebuah persegi panjang dengan simpul ABCD. Di dalamnya, jarak antara titik-titik AC (di diagonal) sama dengan jarak antara titik-titik BD (di diagonal lainnya). Juga, diagonal-diagonal ini bersilangan tepat di tengah.
Oleh karena itu, ketika mencari persegi panjang pada loop tertutup, Anda dapat mencari pasangan titik di ujung segmen garis yang sama yang memotong di tengah. Untuk menemukannya, penting untuk menemukan cara sistematis untuk menggambarkannya.
Untuk memahami apa artinya ini, mari kita mulai dengan sesuatu yang lebih sederhana. Ambil garis angka. Mari kita pilih dua titik di atasnya - katakanlah angka 7 dan 8 - dan buat mereka sebagai satu titik pada bidang numerik (7, 8). Kami juga dapat membangun poin yang merupakan pasangan angka yang identik (7, 7). Sekarang mari kita pertimbangkan semua pasangan angka yang mungkin dapat ditemukan pada garis angka (dan ada banyak dari mereka!). Jika kita membuat semua pasangan angka seperti itu, maka kita akan mengisi seluruh bidang angka. Cara lain untuk menyatakan ini adalah dengan mengatakan bahwa bidang angka "parameterisasi", yaitu, ia mengumpulkan semua pasangan angka pada garis angka secara berurutan.
Vaughn melakukan sesuatu yang serupa dengan pasangan poin pada kurva tertutup. Itu, seperti garis bilangan, satu dimensi, hanya menutup dengan sendirinya. Dia menyadari bahwa jika Anda mengambil pasangan titik dengan kurva, dan membangun sebuah angka dari mereka (dan tidak masalah yang mana koordinat x dan yang mana y), maka pesawat tidak akan bekerja. Sebagai gantinya, Anda mendapatkan angka yang tidak terduga - strip Mobius , permukaan dua dimensi dengan hanya satu sisi.

Dan dalam arti tertentu, ini cukup logis. Untuk memahami alasannya - pilih sepasang titik pada kurva, dan beri nama x dan y. Sekarang pindah dari x ke y, bergerak sepanjang satu bagian dari kurva, dan secara bersamaan - dari y ke x, bergerak di sepanjang yang berlawanan. Dalam prosesnya, Anda akan melewati semua pasangan titik pada kurva, mulai dan berakhir pada pasangan yang tidak berurutan (x, y). Tapi ini akan mengembalikan Anda ke awal - hanya urutan akhir poin akan berlawanan dengan yang awal. Lingkaran titik-titik yang tidak beraturan yang mengubah orientasi ke arah yang berlawanan adalah inti dari strip Möbius.
Pita ini memberikan ahli matematika objek baru yang dapat dianalisis sebagai bagian dari masalah pasak segi empat. Vaughn menggunakan fakta ini untuk membuktikan bahwa pada kurva apa pun setidaknya ada satu set empat titik yang membentuk bujur sangkar.
Jawaban empat dimensi
Bukti Green dan Lobb didasarkan pada karya Vaughn. Namun, ini juga menggabungkan beberapa temuan tambahan, beberapa di antaranya relatif baru. Bukti akhir adalah seperti instrumen yang tepat, hasil yang diinginkan bergantung pada kombinasi ide yang dipertimbangkan dengan cermat.
Salah satu unsur utama pembuktian mereka datang pada November 2019, ketika mahasiswa Universitas Princeton Cole Hugelmeyer menerbitkan makalah tersebut.mendemonstrasikan cara baru menganalisis strip Möbius yang digunakan oleh Vaughn. Ini menggunakan proses matematika yang dikenal sebagai bersarang, yaitu ketika kita mengambil objek dan memproyeksikannya ke ruang geometris. Akibatnya, Green dan Lobb mengambil teknik Hugelmeyer dan memindahkannya ke ruang geometris lain. Tetapi untuk memahami apa yang mereka lakukan, pertama-tama Anda perlu memahami apa yang dia lakukan.
Ini contoh sederhana dari bersarang.
Mari kita mulai dengan garis satu dimensi. Setiap titik garis ditentukan oleh satu angka. Sekarang kita akan menanamkan garis ini dalam ruang dua dimensi - yaitu, kita akan menggambarnya di pesawat.
Setelah menyematkan garis lurus pada bidang xy, setiap titik di dalamnya sudah ditentukan oleh dua angka - koordinat x dan y, yang menggambarkan di mana titik tersebut berada pada bidang. Anda sekarang dapat menganalisis garis menggunakan teknik geometri 2D.
Gagasan Hugelmeier adalah mengambil sesuatu seperti strip Möbius, tetapi menanamkannya dalam ruang 4, di mana sifat-sifat geometri 4-dimensi akan memungkinkan Anda untuk membuktikan hasil yang Anda inginkan.
“Pada dasarnya, kamu memiliki Mobius strip, dan kamu perlu menetapkan empat koordinat untuk setiap titik. Itu akan menjadi sesuatu seperti alamat suatu titik dalam ruang empat dimensi, ”kata Lobb.
Hugelmeyer menetapkan alamat-alamat ini sedemikian rupa sehingga lebih mudah untuk sampai pada tujuan utama, menemukan persegi panjang pada kurva. Kita dapat mengatakan bahwa dia ditugaskan untuk setiap titik pada kurva sesuatu seperti alamat pos - negara bagian, kota, nama jalan dan nomor rumah.
Untuk melakukan ini, ia mulai dari titik tertentu pada strip Mobius dan mengambil dua titik pada kurva tertutup asli yang ditunjukkannya. Kemudian ia menemukan titik tengah segmen garis yang menghubungkan titik-titik ini, dan menentukan koordinat x dan y. Kami mendapat dua nilai pertama dari alamat empat dimensi (negara bagian dan kota).
Dia kemudian mengukur jarak antara dua titik asli pada kurva. Panjang ini menjadi nilai ketiga dari alamat empat dimensi (nama jalan). Akhirnya, ia menghitung sudut antara segmen garis yang menghubungkan dua titik asli dan sumbu x. Sudut ini menjadi nilai keempat dari alamat empat dimensi (nomor rumah). Keempat nilai ini memberi tahu Anda segalanya tentang sepasang titik pada kurva.

Latihan ini kedengarannya cukup menantang, tetapi terbayar dengan cepat. Hugelmeyer mengambil strip Mobius yang terpasang dan memutarnya. Strip Mobius diputar telah bergerak relatif ke posisi semula, dan dua salinan strip berpotongan. Karena belokan terjadi dalam ruang empat dimensi, bentuk persimpangan-sendiri dari jalur Möbius sulit dibayangkan - tetapi mudah untuk dijelaskan secara matematis.
Persimpangan ini sangat penting. Ketika dua salinan strip Mobius ditumpangkan satu sama lain, dua pasang titik dapat ditemukan pada kurva tertutup asli, membentuk empat simpul persegi panjang.
Mengapa?
Pertama, ingatlah bahwa sebuah persegi panjang dapat direpresentasikan sebagai dua pasang titik dengan pusat umum persimpangan segmen dengan panjang yang sama yang menghubungkannya. Informasi inilah yang dikodekan dalam tiga nilai pertama dari alamat empat dimensi yang ditetapkan untuk setiap titik strip Möbius bersarang.
Kedua, dalam ruang empat dimensi, Anda dapat membuka lipatan Möbius sedemikian rupa untuk mengubah hanya satu dari koordinat setiap titik dalam alamat empat dimensi - nomor rumah berubah, tetapi jalan, kota dan negara bagian tetap ada. Sebagai contoh, ingatlah bahwa jika Anda mengambil batu bata, posisikan itu di depan Anda, dan kemudian pindahkan ke kanan, maka hanya koordinat xnya yang akan berubah, tetapi bukan y atau z.
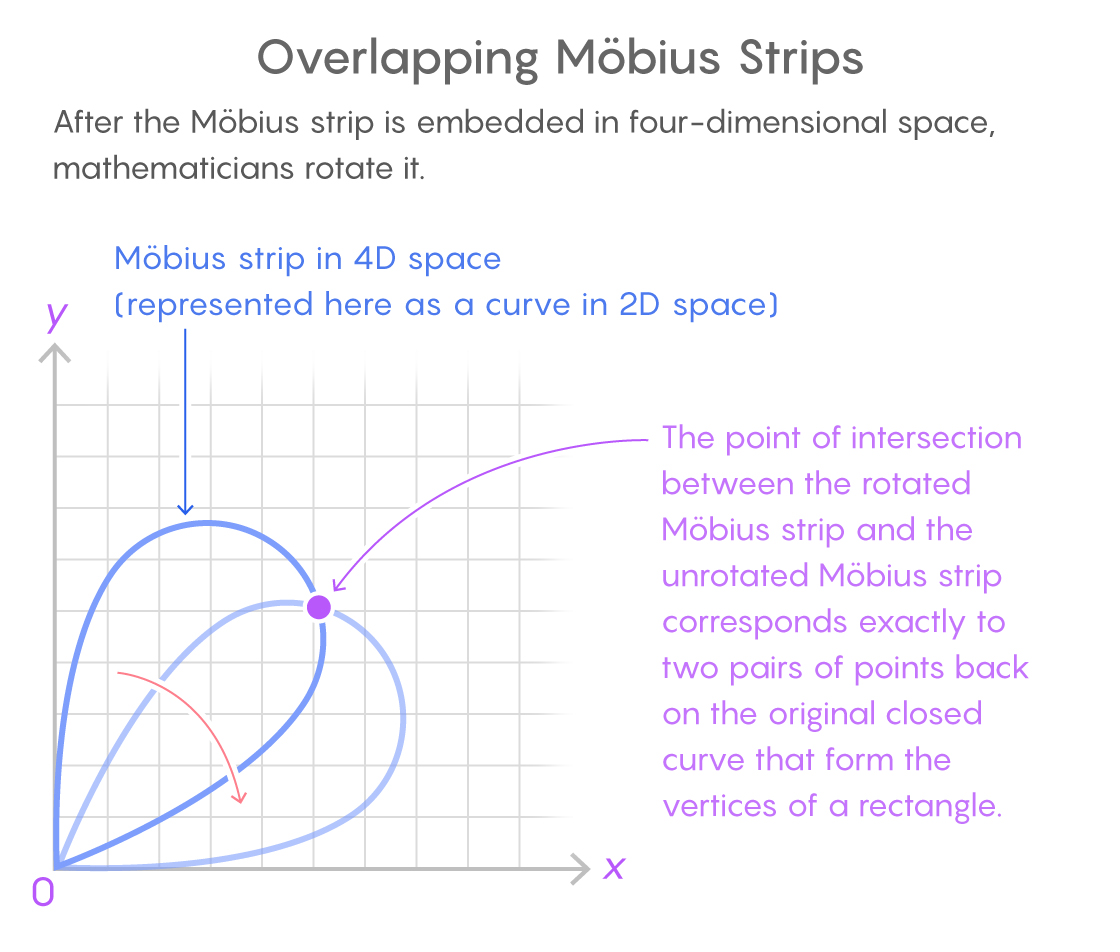
Strip Möbius dalam ruang empat dimensi di sini ditunjukkan oleh kurva dua dimensi. Titik perpotongan dari dua salinan sesuai dengan dua pasang titik pada kurva tertutup asli yang membentuk persegi panjang.
Hugelmeyer menjelaskan cara memutar strip Mobius dalam ruang empat dimensi sehingga dua koordinat yang menunjukkan titik tengah dari garis yang menghubungkan pasangan tidak berubah - seperti halnya koordinat yang menunjukkan jarak antara pasangan poin. Rotasinya hanya mengubah koordinat terakhir - yang berisi informasi tentang sudut di mana segmen yang menghubungkan titik-titik tersebut berada.
Akibatnya, perpotongan salinan Möbius yang dirotasi dan aslinya harus sesuai dengan dua pasang titik yang terletak pada kurva tertutup, memiliki pusat bersama (persimpangan segmen yang menghubungkannya) dan terletak pada jarak yang sama satu sama lain. Yaitu, persimpangan ini berhubungan dengan empat simpul persegi panjang pada kurva.
Strategi menggunakan persimpangan dua ruang untuk menemukan titik yang tepat telah lama digunakan dalam pekerjaan pada masalah pasak persegi dan persegi panjang.
"Di persimpangan ruang-ruang ini adalah yang diinginkan," kata Denn. "Banyak bukti dari sejarah pasak persegi punya ide ini."
Hugelmeyer menggunakan strategi persimpangan dalam lingkungan empat dimensi dan mendapatkan lebih dari siapa pun sebelum dia bisa. Strip Mobius dapat diputar setiap sudut dari 0 ° hingga 360 °, dan ia membuktikan bahwa sepertiga dari semua rotasi ini menghasilkan perpotongan salinan asli dan yang diputar. Ini sama dengan menyatakan bahwa Anda dapat menemukan persegi panjang pada kurva tertutup dengan sepertiga dari semua rasio aspek yang mungkin.
"Kami memberikan penghargaan kepada Cole karena berpikir tentang menempatkan strip Mobius di ruang 4D dan menggunakan teknik 4D," kata Green.
Pada saat yang sama, hasil Hugelmeier ternyata provokatif: jika ruang empat dimensi sangat berguna untuk mengatasi masalah ini, mengapa hanya berguna untuk sepertiga dari semua persegi panjang?
"Bagaimanapun, harus ada cara untuk mendapatkan dua pertiga yang tersisa," kata Green. - Tapi bagaimana caranya?"
Pendekatan symplectic
Green dan Lobb tertarik pada masalah pasak persegi panjang bahkan sebelum pandemi mengirim mereka pulang. Pada bulan Februari, Lobb menyelenggarakan konferensi di Institut Sains dan Teknologi Okinawa , yang juga dihadiri Green. Pasangan itu menghabiskan beberapa hari membicarakan tugas ini. Setelah itu, mereka membahasnya selama seminggu lagi, di sepanjang jalan melihat pemandangan Tokyo.
"Kami belum berhenti membahas masalah ini," kata Lobb. "Kami pergi ke restoran, kafe, museum, dan dari waktu ke waktu kami memikirkan hal ini."
Mereka melanjutkan diskusi mereka bahkan setelah mereka dikunci di rumah mereka. Mereka berharap untuk membuktikan bahwa setiap rotasi strip Mobius akan memberikan titik persimpangan - yang setara dengan menemukan persegi panjang dengan proporsi berapa pun.
Pada pertengahan April, mereka membentuk strategi. Itu berarti menempelkan rekaman itu dalam ruang empat dimensi yang spesial. Bersarang secara teratur menyiratkan bahwa Anda menempatkan objek yang diinginkan dengan cara apa pun. Bayangkan berapa banyak cara Anda dapat menanamkan kurva tertutup satu dimensi dalam bidang dua dimensi - jumlahnya tidak terbatas, karena ada banyak cara di mana Anda dapat menempatkan benang yang diikat dalam lingkaran di atas meja.
Tetapi katakanlah bahwa permukaan dua dimensi tempat Anda bersarang loop memiliki strukturnya sendiri. Bayangkan, misalnya, peta dengan panah (atau vektor) yang menunjukkan kepada kita ke arah mana dan pada kecepatan apa angin bertiup di permukaan Bumi. Sekarang Anda memiliki permukaan 2D dengan informasi tambahan, atau struktur, di setiap titik.
Kemudian Anda dapat memperkenalkan batasan - RFP satu dimensi harus diletakkan di peta sehingga selalu mengikuti petunjuk panah pada peta.
"Anda membatasi hal-hal sehingga kurva mengikuti vektor-vektor ini," kata Schwartz. Dan sekarang Anda memiliki lebih sedikit cara untuk menempatkan kurva.

Ruang geometris lainnya dapat memberikan batasan yang berbeda. Yang penting bagi karya Green dan Lobb adalah yang disebut. ruang symplectic .
Konsep geometris ini pertama kali muncul pada abad ke-19 ketika mempelajari sistem fisik seperti planet yang mengorbit. Posisi sebuah planet bergerak dalam ruang tiga dimensi ditentukan oleh tiga koordinat. Tapi, seperti yang diamati oleh ahli matematika Irlandia William Rowan Hamilton, di setiap titik lintasan gerak planet, Anda juga dapat menempatkan vektor yang menunjukkan momentumnya.
Pada 1980-an, matematikawan Soviet dan Rusia Vladimir Igorevich Arnold mengembangkan studi geometri symplectic . Dia menyadari bahwa ruang geometris dari struktur simpplectic, ketika diputar, berpotongan dengan diri mereka sendiri lebih sering daripada ruang yang tidak memiliki struktur seperti itu.
Ini sempurna untuk Green dan Lobb, karena mereka ingin menyelesaikan masalah pasak segi empat untuk semua proporsi, membuktikan bahwa salinan yang diputar dari strip Mobius yang membuat parameter juga sering berpotongan dengan sendirinya. Jadi mereka mulai mencoba menanamkan strip Möbius dua dimensi dalam ruang symplectic empat dimensi. "Gagasan baru yang radikal adalah untuk mendekati masalah ini dari sudut pandang geometri symplectic," kata Green. "Dan itu mengubah segalanya."
Pada akhir April, Green dan Lobb menentukan bahwa mungkin untuk menanamkan strip Mobius dalam ruang symplectic empat dimensi sehingga akan sejalan dengan strukturnya. Setelah itu, mereka dapat mulai menggunakan alat-alat geometri symplectic, yang banyak di antaranya secara langsung berkaitan dengan pertanyaan tentang persimpangan-diri.
"Jika strip Möbius dapat dibuat untuk mengikuti aturan symplectic, beberapa teorema symplectic dapat digunakan," kata Lobb.
Green dan Lobb yakin bahwa mereka dapat meningkatkan hasil Hugelmeyer - yaitu, membuktikan bahwa persimpangan terjadi tidak hanya di sepertiga dari semua sudut. Ini akan berarti bahwa dari titik-titik kurva akan dimungkinkan untuk membuat persegi panjang dengan lebih dari sepertiga dari semua proporsi yang mungkin.
"Ketika kami mendapat ide ini, menjadi jelas bahwa sesuatu akan terjadi," kata Lobb.
Namun, hasil mereka ternyata lebih umum, dan tampak jauh lebih cepat dari yang mereka harapkan. Semua berkat benda matematika yang aneh - botol Klein , yang dalam konteks geometri symplectic memiliki satu sifat penting.
Koneksi botol Klein
Botol Klein adalah permukaan dua dimensi yang terlihat seperti kendi modernis. Seperti strip Mobius, hanya memiliki satu permukaan, dan dapat dibuat dengan menempelkan dua strip Mobius. Botol Klein apa pun yang dapat Anda kumpulkan dan letakkan di meja Anda (seperti yang dilakukan banyak matematikawan) melintasi dengan sendirinya. Tidak mungkin menempatkan botol Klein di ruang tiga dimensi sehingga tidak melintang dengan sendirinya.
"Botol Klein haruslah permukaan, tetapi pegangannya harus menembus botol untuk pergi dari luar ke dalam," kata Schwartz.
Namun, ini belum tentu demikian. Botol Klein dapat bersarang di ruang 4D sehingga tidak bersinggungan sendiri. Dimensi keempat memberikan ruang untuk bermanuver, dan botol Klein dapat memotong sendiri. Ini dapat dibandingkan dengan bagaimana jika dua orang berjalan satu sama lain dalam garis satu dimensi, mereka tidak dapat menghindari tabrakan, tetapi jika mereka berjalan di lantai dua dimensi, mereka dapat dengan mudah berpaling.

Pada bulan Mei, Green dan Lobb mengingat satu fakta tentang botol Klein - botol itu tidak dapat tertanam dalam ruang symplectic empat dimensi sehingga tidak berpotongan sendiri [dari karya ahli matematika Rusia lainnya, Vsevolod Viktorovich Shevchishintentang Lagrangian embedding botol Klein dalam ruang empat dimensi / kira-kira. diterjemahkan.]. Dengan kata lain, tidak ada botol Klein tanpa persimpangan yang memenuhi semua persyaratan ruang symplectic. Fakta ini menjadi kunci pembuktian. "Itu adalah tongkat ajaib," kata Green.
Dan itulah kenapa. Green dan Lobb telah menunjukkan bahwa mungkin untuk menanamkan strip Mobius dalam ruang symplectic empat dimensi sehingga memenuhi persyaratannya. Mereka hanya perlu mengetahui apakah setiap belokan Mobius strip memotong salinan asli.
Namun, dua strip Mobius berpotongan setara dengan botol Klein, yang memotong dirinya dalam ruang seperti itu. Dan jika Anda memutar strip Mobius sehingga salinan yang diputar tidak bersinggungan dengan aslinya, Anda mendapatkan botol Klein yang tidak bersilangan. Tapi botol Klein semacam itu tidak bisa ada di ruang symplectic empat dimensi. Oleh karena itu, setiap kemungkinan rotasi strip Möbius yang bersarang juga harus berpotongan sendiri - yaitu, pada setiap kurva halus yang tertutup, dapat ditemukan empat titik yang membentuk persegi panjang dengan proporsi apa pun.
Akhir buktinya hits pembaca seperti longsoran salju.
"Ini pertama kali mengatur, mengatur, mengatur, dan kemudian mendengus, dan buktinya sudah siap," kata Denn.
Bukti Green dan Lobb adalah contoh yang baik tentang bagaimana penyelesaian masalah sering bergantung pada menemukan sudut pandang yang benar. Generasi ahli matematika tidak mampu menangani versi masalah pasak segi empat ini karena mereka telah mencoba menyelesaikannya dalam kondisi geometris yang lebih tradisional. Ketika Green dan Lobb membawa masalah ke dunia symplectic, itu mudah diselesaikan.
"Masalah-masalah ini, yang muncul pada 1910-an dan 1920-an, tidak memiliki platform yang cocok untuk merenungkannya," kata Green. "Dan sekarang kita mulai memahami bahwa mereka, pada kenyataannya, adalah inkarnasi tersembunyi dari fenomena symplecticity."