
Artikel lain dalam siklus
Motif untuk menerbitkan teks terperinci seperti itu tentang standar AES adalah untuk memberikan kesempatan untuk membiasakan diri Anda dengan detail, cukup tidak hanya untuk mengembangkan implementasi perangkat lunak independen dari algoritma enkripsi, tetapi juga untuk membuat algoritma untuk kemungkinan serangan cryptanalytic pada cipher, yaitu untuk mendekripsi ciphergram tanpa mengetahui kunci .
Publikasi-publikasi yang tersedia di jaringan tidak memenuhi tujuan-tujuan ini dan tidak dapat saya gunakan dalam proses pelatihan spesialis.
Salah satu persyaratan lama (atau bahkan lama) utama untuk sandi adalah membuat algoritma enkripsi terbuka (dapat diakses untuk studi) dan membungkusnya (mode, protokol, dll.) Semuanya kecuali kunci sandi. Kuncinya adalah sesuatu yang harus dijaga kerahasiaannya dari semua orang. Namun, kuncinya tidak harus memiliki cap tanda tangan "Rahasia". Batas dari kondisi semacam itu hanya penerima sandi yang memiliki kunci, ia sendiri, pada prinsipnya, harus menetapkannya.
Kondisi ini tidak praktis untuk sistem enkripsi simetris. Dan ini adalah perbedaan mendasar antara sistem asimetris (dua kunci) dan yang simetris, di mana sumber kebocoran informasi tentang kunci mungkin bukan satu-satunya. Telah dicatat sebelumnya bahwa AES adalah versi disederhanakan dari cipher RIJNDAEL, dan di sini kita akan menggunakan versi lengkap di beberapa tempat.
AES (Key Schedule).
Memilih kunci saat mengenkripsi pesan adalah tugas yang bertanggung jawab. Pendekatan umum adalah bahwa vektor biner acak dalam ruang vektor multidimensi dipilih dan digunakan untuk kunci tersebut. Seringkali sejumlah algoritma enkripsi dan cipher ditandai dengan adanya kunci yang lemah atau tidak valid, yang terungkap baik selama pengembangan cipher atau selama operasi mereka selama penelitian tambahan. algoritma oleh penulis atau analis kriptografi dan, karenanya, publikasi tentangnya.
Pada gilirannya, ini memberlakukan pembatasan pada prosedur pembuatan kunci, yang tidak diinginkan karena mempersulitnya. Fondasi matematika tentang enkripsi sangat mirip dengan dasar matematika untuk menghasilkan kunci, dan Anda dapat membaca lebih lanjut tentang mereka di sini .
Vektor biner yang dipilih disebut kunci sandi dan dikonversi menjadi “kuadrat” 4x4 = 16 byte. Kemudian kunci bulat dibentuk dari itu menggunakan dua prosedur khusus, yang digunakan dalam proses enkripsi / dekripsi, yang dijelaskan secara rinci di sini .
Satu prosedur disebut Ekspansi Kunci, yang lainnya disebut Pemilihan Kunci Bulat. Vektor acak acak yang dipilih dengan panjang tetap diperluas. Penting juga untuk mempertimbangkan secara hati-hati pilihan generator bilangan acak, untuk menguji dan menyetujui.
Ekspansi kunci
Perasaan memperluas kunci asli (terpilih) terdiri dari membaginya menjadi blok (masing-masing 32 bit) dan kemudian menghasilkan banyak blok baru dengan panjang yang sama untuk setiap putaran.
Jadi, biarkan kunci sandi (128 bit) yang dipilih AES = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c, untuk Nk = 4, yang direpresentasikan dalam blok 4 byte dan ekstensi putaran awal adalah w [0 ] = 2b7e1516; w [1] = 28aed2a6; w [2] = abf71588; w [3] = 09cf4f3c. Simbol w [i] dalam tabel QC, i = 0 (1) 43, menunjukkan kolom 4 byte dari tombol bulat.
Sesi enkripsi adalah persiapan dan transformasi algoritmik pesan, seperti surat. Teks huruf dalam representasi bit dibagi menjadi blok dengan panjang tetap Nb = 128, 192 atau 256 bit. Dalam standar AES, panjang blok hanya 128 bit.
Kemudian setiap blok diwakili oleh kotak atau (kotak dengan 4 baris) dan dienkripsi secara terpisah untuk sejumlah putaran Nr = Nr (Nb, Nk), yang merupakan fungsi dari dua variabel: panjang blok Nb dan panjang kunci Nk, yang dapat secara mandiri mengambil nilai 128, 192, 256 bit.
Pilihan kunci enkripsi tidak memberlakukan batasan pada urutan bit itu sendiri. Setiap putaran Nr menggunakan kunci bulat yang telah dibentuk sebelumnya, atau langsung dihitung, {w [i]}.
Kunci bundar dibentuk dari kunci enkripsi menggunakan algoritma khusus, yang mencakup prosedur Perluasan Kunci dan prosedur Pemilihan Kunci Bulat. Menentukan kunci bundar secara langsung, melewati prosedur ini, tidak dapat diterima.
Inti dan tujuan dari prosedur pertama adalah untuk mengubah kunci enkripsi sumber yang ditentukan menjadi kunci yang lebih panjang dan diperluas (Expanded Key). Jumlah total bit dari kunci yang diperluas dari mana kunci bulat dipilih ditentukan oleh produk K = Nk (Nr + 1) - jumlah bit dalam blok kunci dikalikan dengan jumlah putaran, meningkat satu.
Contoh 1 . Misalkan Nb = Nk = 4, diberikan blok dengan panjang 4 × 32 = 128 bit, lalu Nr = 10.
Panjang K dalam bit untuk kunci yang diperluas adalah K = 128 ∙ 11 = 1408 bit.
Prosedur kedua (Pilihan RoundKey) adalah pemilihan berurutan 32Nk, yaitu 4 kata 32-bit dari kunci yang diperluas, yaitu kunci putaran pertama diwakili oleh kata-kata Nk yang baru dibentuk, kunci putaran kedua diwakili oleh kata-kata Nk berikutnya, dan sebagainya sampai babak terakhir.
Contoh 2. Dengan data awal yang sama (lihat contoh sebelumnya), panjang total kunci yang diperluas dalam byte berisi Nk (Nr + 1) = 4 ∙ 11 = 44 kata empat byte W (i),
i = 0 (1) Nk (Nr + 1) - 1 Baris-baris tabel QC diberi nomor dengan bilangan alami. Baris pertama diberi nomor 4, karena 4 baris (bernomor 0,1,2,3) dengan kunci sandi tidak termasuk dalam tabel QC.
Tabel kunci sandi AES untuk semua 10 putaran (lihat tabel QC di bawah).
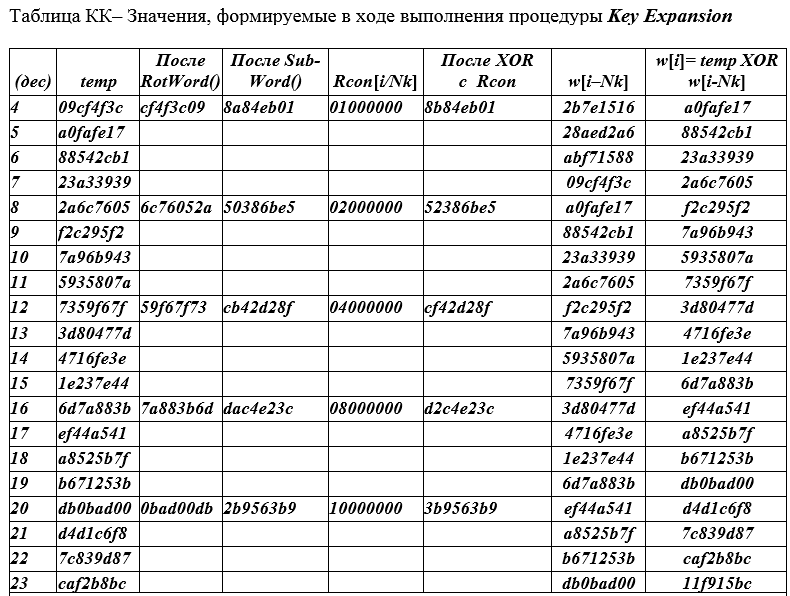
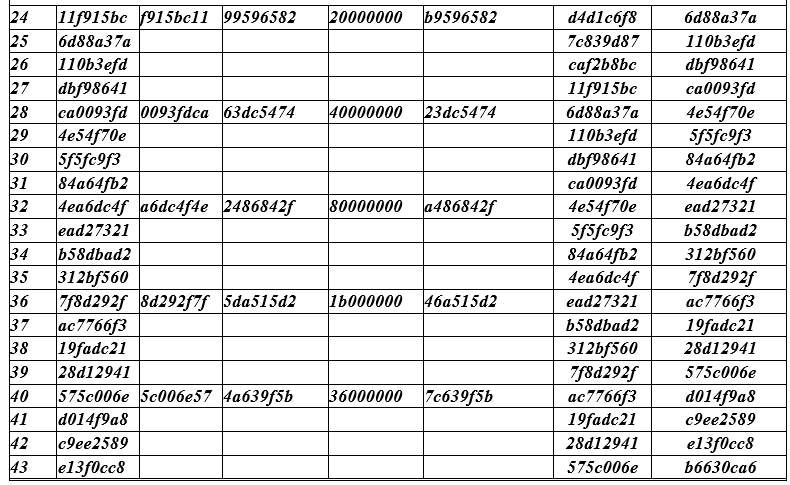
Baris tabel dibagi menjadi kelompok (masing-masing 4 baris). Di setiap grup, semua bidang hanya diisi satu baris teratas. Dalam tiga baris berikutnya, hanya bidang ekstrim (kiri dan kanan) yang diisi. Bidang kiri ( temp ) dari baris berikutnya dan dua berikutnya berisi nilai-nilai yang diambil dari bidang kanan dari garis di atasnya.
Kami memberikan contoh mengisi baris pertama dengan angka i = 4 dari tabel QC. Kolom kiri - nomor baris saat ini dimulai dengan nilai (4) karena nilai 0,1,2,3 pertama tidak termasuk dalam tabel. Secara umum, indeks (nomor baris) i berjalan melalui nilai i = 0 (1) Nk (Nr + 1) -1 atau i = 0 (1) 43 total 44 kata dari 32 digit.
Ke kolom tempnilai w [i-1] = 09cf4f3c ditempatkan dan dengan rotasi (cyclic shift satu byte) RotWord () kita mendapatkan nilai CF4F3C09, yang ditempatkan di kolom 3. Di kolom ke-4 adalah hasil 8A84EB01 menggantikan byte SubBytes dari nilai dari kolom ke-3 dari kolom ke-3 , mis., CF → 8A; 4F → 84; 3C → EB; 09 → 01 => 8A84EV01.
Setiap baris ke-4 dari tabel di kolom ke-5 diisi dengan nilai Rcon [i / Nk], konstanta yang dihitung dengan rumus Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) nilai 01 00 00 00 ditulis dari 4 byte kata, byte pertama adalah 2 0 = 1, yaitu 0000 0001 2 , byte yang tersisa dari kata 32-bit ini adalah nol.
Kolom 6 bidang berisi jumlah (XOR) dari bidang 4 dan 5 8A84EB01 + 01000000 = 8B84EB01;
Kolom 7 kolom berisi W [i - Nk] = W [4 - 4] = W [0] = 2B7E1516;
Kolom 8 kolom berisi jumlah kolom 6 dan 7 kolom W [i = 4] = 884EB01 + 2B7E1516 = A0FAFE17;
Dan sekarang secara rinci dan dengan detail kita akan mempertimbangkan prosedur yang disebutkan.
Prosedur Perluasan Kunci
Mari kita pertimbangkan secara detail prosedur untuk membuat kunci yang diperluas dari kunci sandi asli. Secara formal, kunci W yang diperluas akan dijelaskan oleh urutan blok W [i], i = 0 (1) Nk (Nr + 1) -1, kata-kata 4-byte (tombol bulat) yang terkandung dalam kolom terakhir dari tabel KK, di mana Nk 32-bit pertama kata-kata mewakili kunci asli, yaitu,
W = {W [0], W [1], W [2], W [3], W [4], ..., W [K-1]}
Selanjutnya i-th kata-kata dibentuk secara rekursif dari kata-kata sebelumnya sesuai dengan ekspresi di mana penjumlahannya adalah XOR.
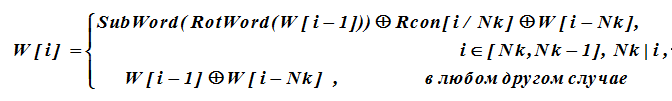 .
.
Untuk kata-kata W [i] dari kunci, indeks yang merupakan kelipatan dari Nk, nilai-nilai W [i-1] mengalami transformasi tambahan sebelum melakukan operasi XOR. Transformasi ini dijelaskan sebagai berikut.
Deskripsi transformasi berisi fungsi:
RotWord () - byte pergantian siklik dari 32-bit kata a (0) a (1) a (2) a (3) sesuai dengan aturan
{a (0) a (1) a (2) a (2) a (3)} → {a (3) a (0) a (1) a (2)};
SubWord () - penggantian byte a (j) dengan elemen S-box dari fungsi SubBytes (), misalnya, byte (af) diganti dengan byte s (a, f) dari S-box; tindakannya sama dengan saat memproses pesan,
Rcon [j] - istilah XOR sama dengan 2 j-1 .

Posisi yang disorot adalah kelipatan Nb, nilai-nilai yang dibentuk menggunakan fungsi SubWord (), RotWord (), Rcon (). Posisi W [0] –W [3] diisi sesuai dengan data awal yang diberikan, semua yang berikutnya dihitung dengan rasio untuk W [i].
Seleksi Kunci Bulat
Pilihan tombol bulat (RoundKeySelection). Untuk putaran saat ini dengan nomor r. Tombol bulat dipilih sebagai {W [Nb (r) -1], ..., W [Nb (r + 1) - 1]},
r = 1 (1) Nr.
Di sini kita perhatikan bahwa algoritma enkripsi umum menyediakan untuk varian yang berbeda dari set variabel Nb, Nk, Nr. Untuk implementasi spesifik dari opsi tetap, ini dapat sangat disederhanakan. Tombol bulat dapat dihitung dengan cepat, yang tidak memerlukan banyak memori untuk menyimpan seluruh urutan W. Anda dapat membatasi diri Anda pada buffer kata-kata Nk.
Contoh 3 . Mari kita jelaskan proposisi teoretis yang diberikan dengan contoh numerik. Biarkan, seperti sebelumnya, Nb = Nk = 4, Nr = 10. Kunci sandi diberikan sebagai urutan heksadesimal K = 2b7e1516 282ed2a6 abf71588 09cf4f3c

Arsitektur "kuadrat" dan komputasi berorientasi byte didefinisikan oleh tabel berikut.
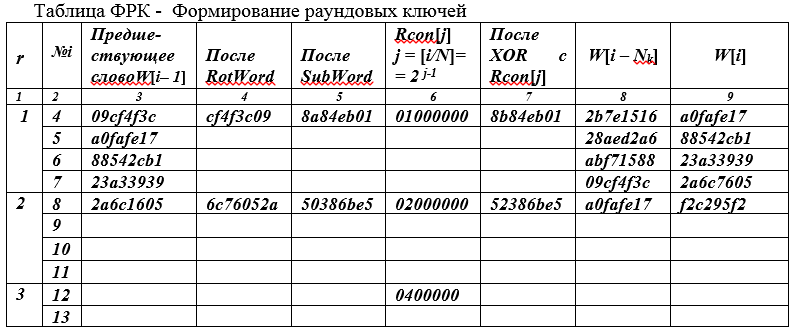
Kolom kiri ditambahkan pada tabel - angka bulat (r).
Pada baris pertama r = 1, i = 4, byte sebelumnya W [i-1] = W [3] ditulis dalam kolom ketiga. byte terakhir dari kunci cipher K. Karena indeks i = 4 adalah kelipatan dari Nk = 4, maka dalam kolom 6 kita menulis (Rcon (J) = 01000000, j = [i / Nk] = 2 j-1 = 2 0 = 1) nilai 01 00 00 00 4- ditulis kata x byte, byte pertama adalah 2 0 = 1, yaitu 0000 0001, byte yang tersisa dari kata 32-bit ini adalah nol.
Di kolom keempat tabel, kita memasukkan nilai dari kolom sebelumnya, tetapi secara siklis bergeser 1 byte ke kiri (rotasi kata - RotWord). Kolom kelima berisi hasil penggantian byte dari nilai-nilai kolom sebelumnya dengan nilai-nilai byte dari blok-S (fungsi SubWord - ganti byte). Setelah itu, penambahan mod2 (XOR) dari isi kolom 5 dan 6 dilakukan, 8a84eb01 + 0100 0000 = 8b84eb01, dan hasil penjumlahan dimasukkan ke dalam kolom 7.
Dalam representasi biner dari byte 0000 0001 2 = 01, 16 bit paling signifikan terletak di sebelah kanan.
Kolom 8 berisi nilai kata W [i-Nk] = W [0] (untuk baris pertama, ini adalah nilai kata byte pertama (byte kiri) dari kunci enkripsi W [0]), yang ditambahkan oleh operasi XOR 8b 84 eb 01+ 2b 7e 15 16 = a0 fa fe 17 dengan isi 7 kolom. Hasil penjumlahan (kolom 9) hanyalah yang pertama dari empat, 4-byte kata kunci putaran dari putaran pertama.
Tiga kata lain dari kunci putaran dari putaran pertama dibentuk tanpa menggunakan fungsi dari pergantian siklik, penggantian dan Rcon [j], karena jumlahnya bukan kelipatan Nk. Isi kolom 9 ditransfer ke kolom ketiga dari baris tabel berikutnya.
Definisi Rcon [j]. Prosedur ini dilakukan sesuai dengan algoritma khusus, tindakan yang akan kami ilustrasikan dengan contoh. Argumen j dari fungsi Rcon [j] adalah bilangan bulat dan ditentukan oleh nilai saat ini dari variabel i - jumlah kata kunci. Jelas
j = 1, 2, 3,… untuk i = Nk, 2Nk, 3Nk,….
Karena Nk dalam contoh kita adalah 4, kita memiliki nilai integer j untuk i = 4, 8, 12. Selanjutnya, untuk setiap integer j Rcon [j] = 2 j-1 = 1, 2, 4, 8, 16, ....
Penggandaan nilai diperbolehkan selama Rcon [j] adalah elemen dari bidang GF (2 8 ).
Untuk i> 32 kita mendapat j> 8. Nilai di luar bidang harus dikembalikan ke bidang. Ini dicapai dengan mengurangi representasi polinomial dari unsur-unsur bidang Rcon [j] (modφ (x)).
Contoh 4... Biarkan i = 32, 36, 40. Lalu j = 8, 9, 10. Nilai-nilai ini berada di luar bidang. Kami mengembalikannya ke bidang dengan mengurangi modulo φ (x) dan menghitung nilai yang diperlukan.
Kami mendefinisikan nilai Rcon [j] yang sesuai. Hasil perhitungan dirangkum dalam sebuah tabel.

Ini dapat melengkapi pertimbangan langkah-langkah untuk menghasilkan kunci sandi AES bulat.