FAISS: Cepat menemukan wajah dan klon pada data multi-juta dolar

Suatu hari, pada malam konferensi klien, yang diadakan setiap tahun oleh grup DAN, kami memikirkan hal-hal menarik apa yang dapat kami pikirkan sehingga mitra dan klien kami akan memiliki kesan dan kenangan yang menyenangkan dari acara tersebut. Kami memutuskan untuk menganalisis arsip ribuan foto dari konferensi ini dan beberapa yang lalu (dan ada 18 foto pada saat itu): seseorang mengirimkan fotonya kepada kami, dan dalam beberapa detik kami mengirimkan kepadanya sejumlah foto bersamanya dari arsip kami selama beberapa tahun.



Kami tidak menciptakan sepeda, kami mengambil perpustakaan dlib yang terkenal dan menerima embeddings (representasi vektor) dari setiap orang. 



Kami menambahkan bot Telegram untuk kenyamanan, dan semuanya baik-baik saja. Dari sudut pandang algoritma pengenalan wajah, semuanya bekerja dengan baik, tetapi konferensi berakhir, dan saya tidak ingin berpisah dengan teknologi yang telah dicoba dan diuji. Dari beberapa ribu orang saya ingin pergi ke ratusan juta, tetapi kami tidak memiliki tugas bisnis tertentu. Setelah beberapa waktu, kolega kami memiliki tugas yang mengharuskan bekerja dengan data dalam jumlah besar.



Pertanyaannya adalah untuk menulis sistem pemantauan bot pintar di dalam jaringan Instagram. Di sini pemikiran kami memunculkan pendekatan yang sederhana dan kompleks:



Cara sederhana: Kami menganggap semua akun yang memiliki lebih banyak langganan daripada pelanggan, tidak ada avatar, nama lengkap tidak diisi, dll. Akibatnya, kami mendapatkan kerumunan akun setengah mati yang tidak dapat dipahami.



Cara yang sulit: Karena bot modern telah menjadi jauh lebih pintar, dan sekarang mereka memposting posting, tidur, dan bahkan menulis konten, muncul pertanyaan: bagaimana cara menangkap ini? Pertama-tama, pantau teman-teman mereka, seperti juga bot, dan lacak foto rangkap. Kedua, jarang ada bot yang tahu cara membuat gambarnya sendiri (meskipun ini mungkin), yang berarti bahwa duplikat foto orang di berbagai akun di Instagram merupakan pemicu yang baik untuk menemukan jaringan bot.

Apa berikutnya?

Jika jalur sederhana cukup dapat diprediksi dan dengan cepat memberikan beberapa hasil, maka jalur yang sulit sulit justru karena untuk mengimplementasikannya kita harus membuat vektor dan mengindeks volume foto yang sangat besar untuk perbandingan kemiripan berikutnya - jutaan, dan bahkan milyaran. Bagaimana cara mempraktikkannya? Bagaimanapun, masalah teknis muncul:

1. Kecepatan dan akurasi pencarian
2. Disk Space Digunakan oleh Data
3. Ukuran memori RAM yang digunakan. 

Jika hanya ada beberapa foto, setidaknya tidak lebih dari sepuluh ribu, kita dapat membatasi diri pada solusi sederhana dengan pengelompokan vektor, tetapi untuk bekerja dengan volume besar vektor dan menemukan tetangga terdekat ke vektor tertentu, diperlukan algoritma yang kompleks dan dioptimalkan.



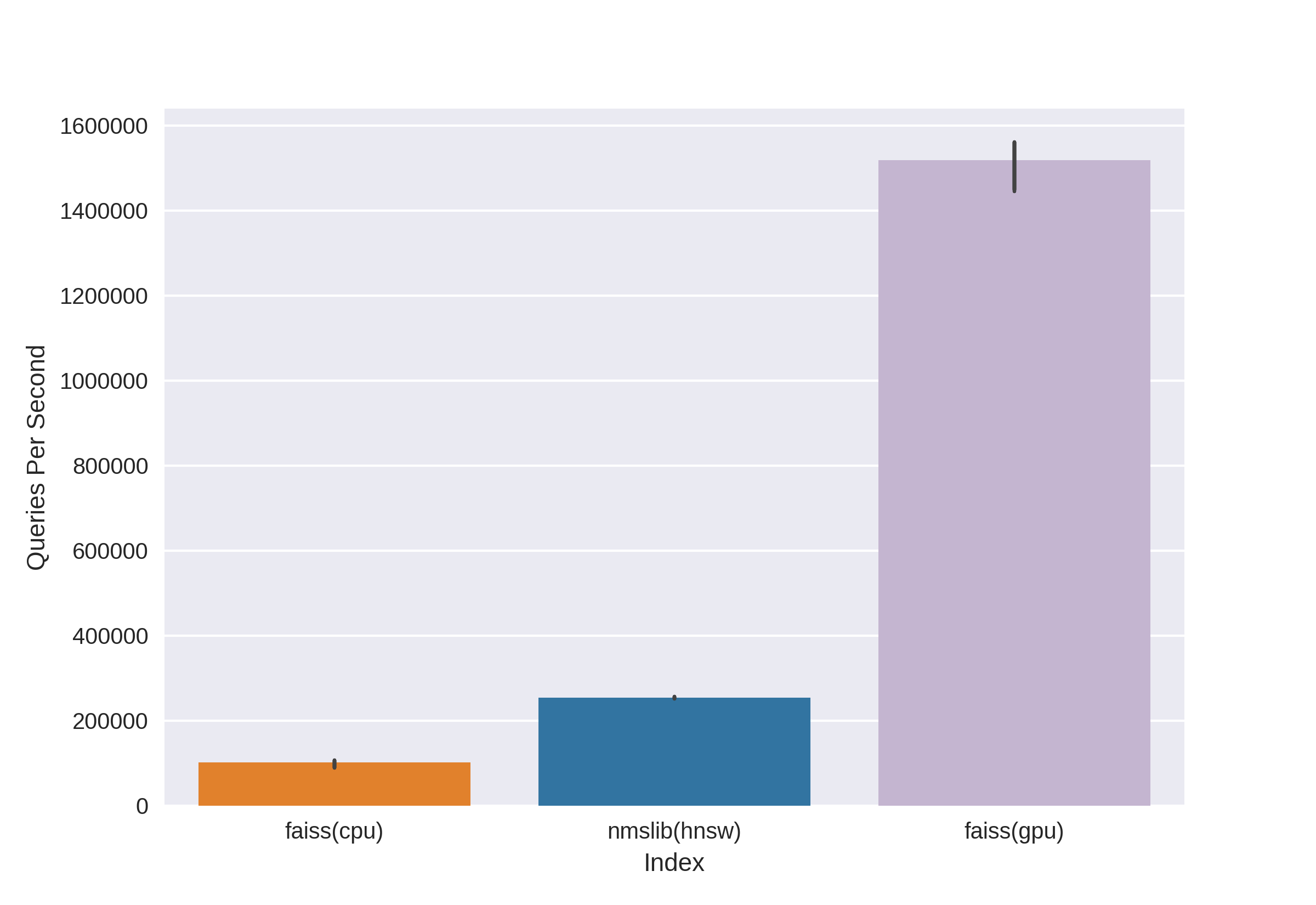
Ada teknologi terkenal dan terbukti, seperti Annoy, FAISS, HNSW. Algoritme pencarian tetangga HNSW cepat tersedia di pustaka nmslib dan hnswlib, menunjukkan hasil mutakhir pada CPU, yang dapat dilihat dari tolok ukur yang sama. Tetapi kami langsung memutusnya, karena kami tidak puas dengan jumlah memori yang digunakan ketika bekerja dengan jumlah data yang sangat besar. Kami mulai memilih antara Annoy dan FAISS dan akhirnya memilih FAISS karena kenyamanannya, penggunaan memori yang lebih sedikit, potensi penggunaan pada GPU dan tolok ukur kinerja (Anda dapat melihat, misalnya, di sini ). Omong-omong, dalam FAISS, algoritma HNSW diimplementasikan sebagai opsi.

Apa itu FAISS?

Pencarian Kesamaan Penelitian AI Facebook - Dikembangkan oleh tim Penelitian AI Facebook untuk dengan cepat menemukan tetangga terdekat dan mengelompokkan dalam ruang vektor. Kecepatan pencarian yang tinggi memungkinkan bekerja dengan data yang sangat besar - hingga beberapa miliar vektor.



Keuntungan utama FAISS adalah hasil mutakhirnya pada GPU, sementara implementasinya pada CPU sedikit lebih rendah daripada hnsw (nmslib). Kami ingin dapat mencari CPU dan GPU. Selain itu, FAISS dioptimalkan dalam hal penggunaan memori dan pencarian dalam jumlah besar.



Sumber



FAISS memungkinkan Anda dengan cepat mencari k vektor terdekat untuk vektor yang diberikan x. Tetapi bagaimana cara kerja pencarian ini di bawah tenda?

Indeks

Konsep utama dalam FAISS adalah indeks , dan pada dasarnya itu hanya kumpulan parameter dan vektor. Set parameter sangat berbeda dan bergantung pada kebutuhan pengguna. Vektor dapat tetap tidak berubah, tetapi dapat dibangun kembali. Beberapa indeks tersedia untuk pekerjaan segera setelah menambahkan vektor, dan beberapa memerlukan pelatihan sebelumnya. Nama vektor disimpan dalam indeks: baik dalam penomoran dari 0 hingga n, atau sebagai angka yang cocok dengan tipe Int64.



Indeks pertama, dan yang paling sederhana yang kami gunakan di konferensi, adalah Flat . Hanya menyimpan semua vektor dalam dirinya sendiri, dan pencarian untuk vektor yang diberikan dilakukan oleh pencarian lengkap, sehingga Anda tidak perlu melatihnya (tetapi tentang belajar di bawah). Pada sejumlah kecil data, indeks sederhana semacam itu mungkin dapat memenuhi kebutuhan pencarian Anda.



Contoh:

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

Buat indeks Flat dan tambahkan vektor tanpa pelatihan:

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

Sekarang mari kita cari 7 tetangga terdekat untuk lima vektor pertama dari vektor:

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

Kita melihat bahwa tetangga terdekat dengan jarak 0 adalah vektor itu sendiri, sisanya berdekatan dengan meningkatnya jarak. Mari mencari vektor kami dari kueri:

D, I = index.search(query, topn) 
print(I)
print(D)

Sekarang jarak di kolom pertama hasilnya tidak nol, karena vektor dari kueri tidak ada dalam indeks.



Indeks dapat disimpan ke disk dan kemudian diunduh dari disk:

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

Tampaknya semuanya dasar! Beberapa baris kode - dan kami sudah memiliki struktur untuk mencari vektor dimensi tinggi. Tetapi indeks seperti itu dengan hanya puluhan juta vektor dimensi 512 akan berbobot sekitar 20GB dan memakan banyak RAM saat digunakan.



Dalam proyek konferensi, kami menggunakan pendekatan dasar dengan indeks datar, semuanya hebat karena jumlah data yang relatif kecil, tetapi sekarang kita berbicara tentang puluhan dan ratusan juta vektor dimensi tinggi!

Percepat pencarian Anda dengan daftar terbalik

Sumber



Fitur utama dan paling keren dari FAISS adalah indeks IVF, atauindeks File Terbalik . Gagasan tentang file-file yang terbalik adalah singkat, dan dijelaskan dengan indah di jari :



Mari kita bayangkan pasukan raksasa yang terdiri dari prajurit paling beraneka ragam, berjumlah, katakanlah, 1.000.000 orang. Memerintah seluruh pasukan sekaligus tidak akan mungkin. Seperti kebiasaan dalam urusan militer, kita perlu membagi pasukan kita menjadi sub-unit. Mari kita bagi$$$\sqrt{1 000 000} = 1000$kira-kira bagian yang sama, memilih untuk peran komandan perwakilan dari setiap unit. Dan kami akan mencoba mengirim yang paling mirip dalam karakter, asal, data fisik, dll. prajurit dalam satu unit, dan kami akan memilih komandan sehingga ia mewakili unitnya seakurat mungkin - ia adalah seseorang "rata-rata". Akibatnya, tugas kami berkurang dari memerintahkan satu juta tentara menjadi komandan 1.000 unit melalui komandan mereka, dan kami memiliki ide yang bagus tentang komposisi pasukan kami, karena kami tahu seperti apa komandan itu.



Ini adalah ide di balik indeks IVF: mari kita kelompokkan satu set besar vektor sepotong demi sepotong menggunakan algoritma k-means, pengaturan setiap bagian sesuai dengan centroid, adalah vektor yang merupakan pusat yang dipilih untuk cluster yang diberikan. Pencarian akan dilakukan melalui jarak minimum ke centroid, dan hanya dengan demikian kita akan mencari jarak minimum di antara vektor-vektor di cluster yang sesuai dengan centroid ini. Mengambil k sama$$$\sqrt{n}$dimana $$$n$ - jumlah vektor dalam indeks, kami mendapatkan pencarian optimal pada dua level - pertama di antara $$$\sqrt{n}$ centroid lalu di antara $$$\sqrt{n}$vektor di setiap cluster. Pencarian jauh lebih cepat daripada pencarian brute force, yang memecahkan salah satu masalah kita ketika bekerja dengan jutaan vektor.





Ruang vektor dibagi dengan metode k-means ke dalam k cluster. Setiap cluster diberi



kode Contoh centroid :

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

Dan Anda dapat menulisnya jauh lebih elegan, menggunakan hal FAISS yang nyaman untuk membangun indeks:

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

Setelah mempertimbangkan jenis indeks ini setelah Flat, kami memecahkan salah satu masalah potensial kami - kecepatan pencarian, yang menjadi beberapa kali lebih lambat dibandingkan dengan pencarian penuh.

D, I = index.search(query, topn) 
print(I)
print(D)

Tetapi ada satu "tetapi" - akurasi pencarian, serta kecepatan, akan tergantung pada jumlah cluster yang dikunjungi, yang dapat diatur menggunakan parameter nprobe:

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

Seperti yang Anda lihat, setelah meningkatkan nprobe, kami memiliki hasil yang sangat berbeda, bagian atas jarak terpendek dalam D menjadi lebih baik.



Anda dapat mengambil nprobe sama dengan jumlah centroid dalam indeks, maka itu akan setara dengan pencarian brute force, akurasinya akan menjadi yang tertinggi, tetapi kecepatan pencarian akan terasa menurun.

Mencari disk - Pada Daftar Disk yang Terbalik

Hebat, kami memecahkan masalah pertama, sekarang kami mendapatkan kecepatan pencarian yang dapat diterima pada puluhan juta vektor! Tapi semua ini tidak berguna selama indeks besar kami tidak masuk ke dalam RAM.



Khusus untuk tugas kami, keuntungan utama FAISS adalah kemampuan untuk menyimpan Daftar Terbalik dari indeks IVF pada disk, hanya memuat metadata ke dalam RAM.



Bagaimana kita membuat indeks seperti itu: kita melatih indexIVF dengan parameter yang diperlukan pada jumlah data maksimum yang mungkin masuk ke dalam memori, kemudian menambahkan vektor (mereka yang telah dilatih dan tidak hanya) ke indeks terlatih dalam bagian-bagian dan menulis indeks untuk masing-masing bagian ke disk.

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

Kami melatih indeks pada GPU dengan cara ini:

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu (res, 0, index_flat) dapat diganti dengan faiss.index_cpu_to_all_gpus (index_flat) untuk menggunakan semua GPU secara bersamaan.



Sangat diinginkan bahwa sampel pelatihan harus representatif mungkin dan memiliki distribusi yang seragam, jadi kami melakukan pra-penyusunan dataset pelatihan dari jumlah vektor yang diperlukan, memilihnya secara acak dari seluruh dataset.

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

Setelah itu, kami menggabungkan semua Daftar Invert bersama. Ini dimungkinkan, karena masing-masing blok pada dasarnya adalah indeks terlatih yang sama, hanya dengan vektor yang berbeda di dalamnya.

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

Intinya: sekarang indeks kami adalah file populated.index dan merged_blocks.ivfdata .



The populated.index berisi path lengkap asli untuk file dengan Lists Inverted, jadi jika jalan menuju perubahan file ivfdata untuk beberapa alasan, ketika membaca indeks, Anda akan perlu menggunakan faiss.IO_FLAG_ONDISK_SAME_DIR bendera , yang memungkinkan Anda untuk mencari file ivfdata di direktori yang sama seperti populated.index:

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

Contoh demo dari proyek FAISS Github diambil sebagai dasar .



Panduan mini indeks indeks dapat dilihat di Wiki FAISS . Sebagai contoh, kami dapat memasukkan dataset pelatihan 12 juta vektor ke dalam RAM, jadi kami memilih indeks IVFFlat pada 262144 centroid untuk kemudian ditingkatkan hingga ratusan juta. Panduan ini juga mengusulkan untuk menggunakan indeks IVF262144_HNSW32, di mana vektor milik klaster ditentukan oleh algoritma HNSW dengan 32 tetangga terdekat (dengan kata lain, IndexHNSWFlat quantizer digunakan), tetapi, seperti yang terlihat bagi kami selama pengujian lebih lanjut, pencarian untuk indeks tersebut kurang akurat. Selain itu, harus diingat bahwa quantizer semacam itu mengecualikan kemungkinan menggunakannya pada GPU.

Mengurangi Penggunaan Disk secara dramatis dengan Kuantisasi Produk

Berkat metode pencarian disk, dimungkinkan untuk menghapus beban dari RAM, tetapi indeks dengan sejuta vektor masih membutuhkan sekitar 2 GB ruang disk, dan kami berbicara tentang kemungkinan bekerja dengan miliaran vektor, yang akan membutuhkan lebih dari dua TB! Tentu saja, volumenya tidak terlalu besar jika Anda menetapkan tujuan dan mengalokasikan ruang disk tambahan, tetapi sedikit mengganggu kami.



Dan di sini pengkodean vektor datang untuk menyelamatkan, yaitu Skalar Quantization (SQ) dan Product Quantization (PQ)... SQ adalah pengkodean setiap komponen vektor dengan n bit (biasanya 8, 6 atau 4 bit). Kami akan mempertimbangkan opsi PQ, karena gagasan pengkodean satu komponen float32 dengan delapan bit terlihat terlalu menyedihkan dalam hal kehilangan akurasi. Meskipun dalam beberapa kasus, mengompresi SQfp16 ke float16 akan memiliki akurasi yang hampir tidak ada kerugiannya.



Inti dari Kuantisasi Produk adalah sebagai berikut: vektor dimensi 512 dibagi menjadi n bagian, yang masing-masing dikelompokkan menjadi 256 kluster yang mungkin (1 byte), yaitu kami mewakili vektor dengan n byte, di mana n biasanya paling banyak 64 dalam implementasi FAISS. Tetapi kuantisasi semacam itu diterapkan bukan pada vektor-vektor dari dataset itu sendiri, tetapi pada perbedaan vektor-vektor ini dan centroid terkait yang diperoleh selama pembuatan Daftar Terbalik! Ternyata Daftar yang Terbalik akan dikodekan set jarak antara vektor dan centroid mereka.

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

Ternyata sekarang kita tidak perlu menyimpan semua vektor - itu sudah cukup untuk mengalokasikan n byte per vektor dan 2048 byte per vektor centroid. Dalam kasus kami, kami ambil$$$n = 64$, yaitu $$$\frac{512}{64} = 8$- panjang satu sub-vektor, yang didefinisikan dalam salah satu dari 256 cluster.







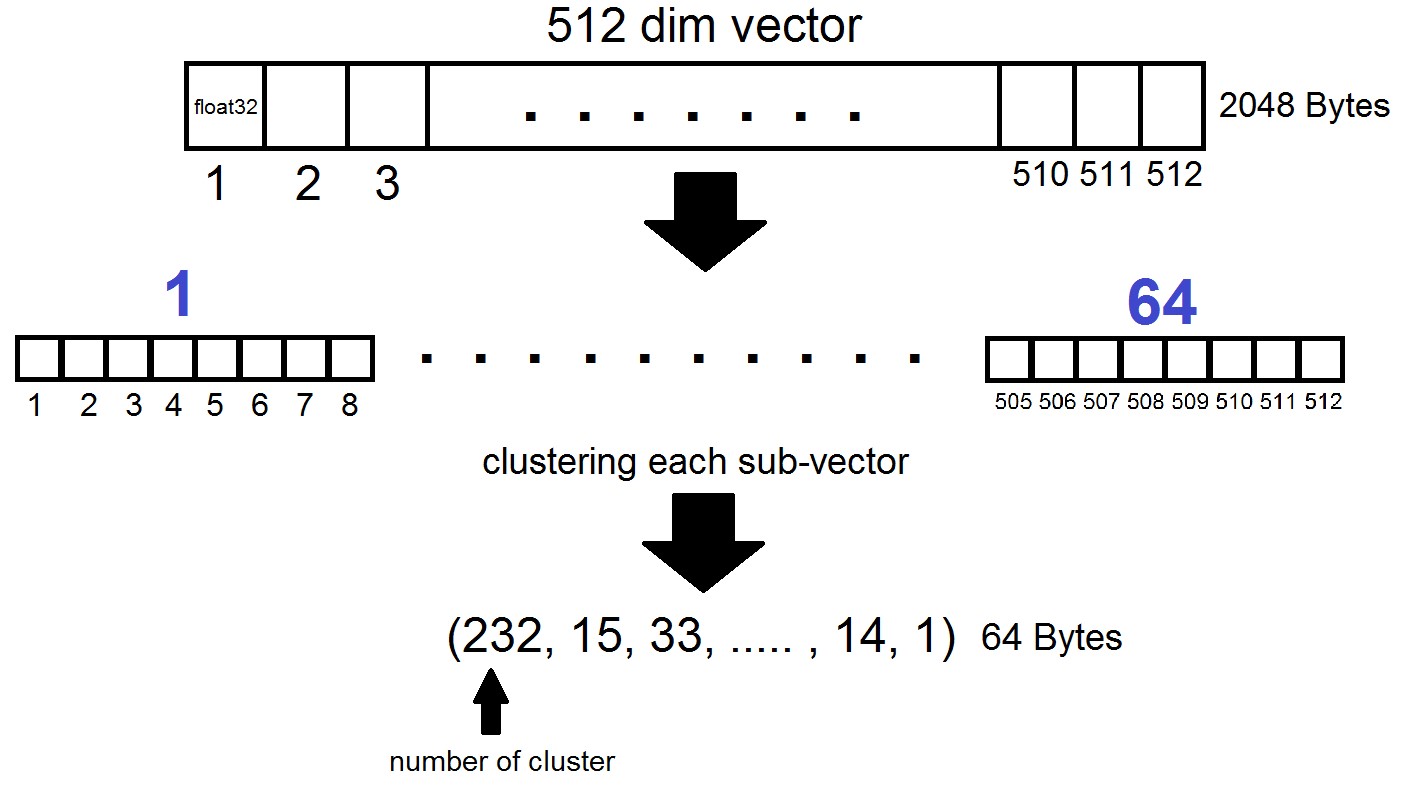
Ketika mencari dengan vektor x, centroid terdekat akan ditentukan pertama dengan Flat quantizer biasa, dan kemudian x juga dibagi menjadi sub-vektor, yang masing-masing dikodekan dengan jumlah salah satu dari 256 centroid yang sesuai. Dan jarak ke vektor didefinisikan sebagai jumlah dari 64 jarak antara sub-vektor.

Apa intinya?

Kami menghentikan percobaan kami pada indeks "IVF262144, PQ64", karena sepenuhnya memenuhi semua kebutuhan kami akan kecepatan dan akurasi pencarian, dan juga memastikan penggunaan ruang disk yang wajar dengan penskalaan indeks lebih lanjut. Lebih khusus lagi, saat ini, dengan 315 juta vektor, indeks ini menempati 22 GB ruang disk dan sekitar 3 GB RAM saat digunakan.



Detail menarik lainnya yang tidak kami sebutkan sebelumnya adalah metrik yang digunakan oleh indeks. Secara default, jarak antara dua vektor dihitung dalam metrik L2 Euclidean, atau dalam bahasa yang lebih dimengerti, jarak dihitung sebagai akar kuadrat dari jumlah kuadrat dari perbedaan koordinat-bijaksana. Tetapi Anda dapat menentukan metrik lain, khususnya, kami menguji metrik METRIC_INNER_PRODUCT, atau metrik jarak cosinus antara vektor. Itu adalah kosinus karena kosinus sudut antara dua vektor dalam sistem koordinat Euclidean dinyatakan sebagai rasio produk skalar (berdasarkan koordinat) vektor dengan produk dari panjangnya, dan jika semua vektor di ruang kita memiliki panjang 1, maka kosinus sudut akan persis sama dengan produk koordinat koordinat. Dalam hal ini, semakin dekat vektor dalam ruang, semakin dekat dengan satu titik produknya.



Metrik L2 memiliki transisi matematis langsung ke metrik produk skalar. Namun, ketika secara eksperimental membandingkan dua metrik, kesannya adalah bahwa metrik produk titik membantu kami menganalisis koefisien kesamaan gambar dengan cara yang lebih baik. Selain itu, hiasan foto kami diperoleh dengan menggunakanInsightFace , yang mengimplementasikan arsitektur ArcFace menggunakan jarak kosinus. Ada juga metrik lain dalam indeks FAISS yang dapat Anda baca di sini .

Kesimpulan dan contoh menarik

Jadi, kembali ke tempat semuanya dimulai. Dan itu dimulai, ingat, dengan motivasi untuk memecahkan masalah menemukan bot di jaringan Instagram, dan lebih khusus lagi - untuk mencari pos duplikat dengan orang atau avatar di set pengguna tertentu. Dalam proses penulisan materi, menjadi jelas bahwa deskripsi terperinci tentang metodologi kami untuk mencari bot akan membutuhkan artikel terpisah, yang akan kami bahas dalam publikasi berikut, tetapi untuk saat ini kami akan membatasi diri pada contoh percobaan kami dengan FAISS.



Anda dapat membuat vektor gambar atau wajah dengan cara yang berbeda, kami telah memilih teknologi InsightFace (membuat vektor gambar dan mengekstraksi fitur n-dimensi dari mereka adalah cerita panjang yang terpisah). Dalam perjalanan percobaan dengan infrastruktur yang kami peroleh, properti yang cukup menarik dan lucu ditemukan.



Misalnya, dengan seizin kolega dan kenalan, kami mengunggah wajah mereka dalam pencarian dan dengan cepat menemukan foto-foto tempat mereka hadir:





Rekan kami masuk ke foto pengunjung Comic-Con, dengan latar belakang kerumunan. Sumber





Piknik dalam grup besar teman, foto dari akun teman. Sumber





Baru saja lewat. Seorang fotografer yang tidak dikenal menangkap mereka untuk profil tematiknya. Mereka tidak tahu ke mana foto mereka pergi, dan setelah 5 tahun mereka benar-benar lupa bagaimana mereka difoto. Sumber





Dalam hal ini, fotografer tidak dikenal dan difoto diam-diam!

Saya langsung ingat seorang gadis yang mencurigakan dengan kamera refleks, duduk berseberangan pada saat itu :) Source



Dengan demikian, melalui tindakan sederhana, FAISS memungkinkan Anda untuk mengumpulkan analog dari FindFace yang terkenal.



Fitur menarik lainnya: dalam indeks FAISS, semakin banyak wajah yang mirip satu sama lain, semakin dekat satu sama lain vektor yang sesuai dalam ruang berada. Saya memutuskan untuk melihat lebih dekat pada hasil pencarian yang sedikit kurang akurat untuk wajah saya dan menemukan klon yang sangat mirip :)





Beberapa klon penulis.

Sumber Foto: 1 , 2 ,  3



Secara umum, FAISS membuka bidang besar untuk implementasi setiap ide kreatif. Misalnya, menggunakan prinsip kedekatan vektor yang sama dari wajah yang sama, seseorang dapat membangun jalur dari satu orang ke orang lain. Atau, sebagai upaya terakhir, buat FAISS sebagai pabrik untuk memproduksi meme seperti itu:





Sumber



Terima kasih atas perhatian Anda dan kami berharap materi ini bermanfaat bagi pembaca Habr!



Artikel ini ditulis dengan dukungan rekan-rekan saya Artyom Korolev (korolevart), Timur Kadyrov dan Arina Reshetnikova.



R&D Dentsu Aegis Network Rusia.